电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》研究生课程教学资源（课件讲稿）第20讲 有源滤波器综合基础（高阶有源滤波器）

第20讲高阶有源滤波器 第十章有源滤波器综合基础(2)

第20讲 高阶有源滤波器 第十章 有源滤波器综合基础(2)

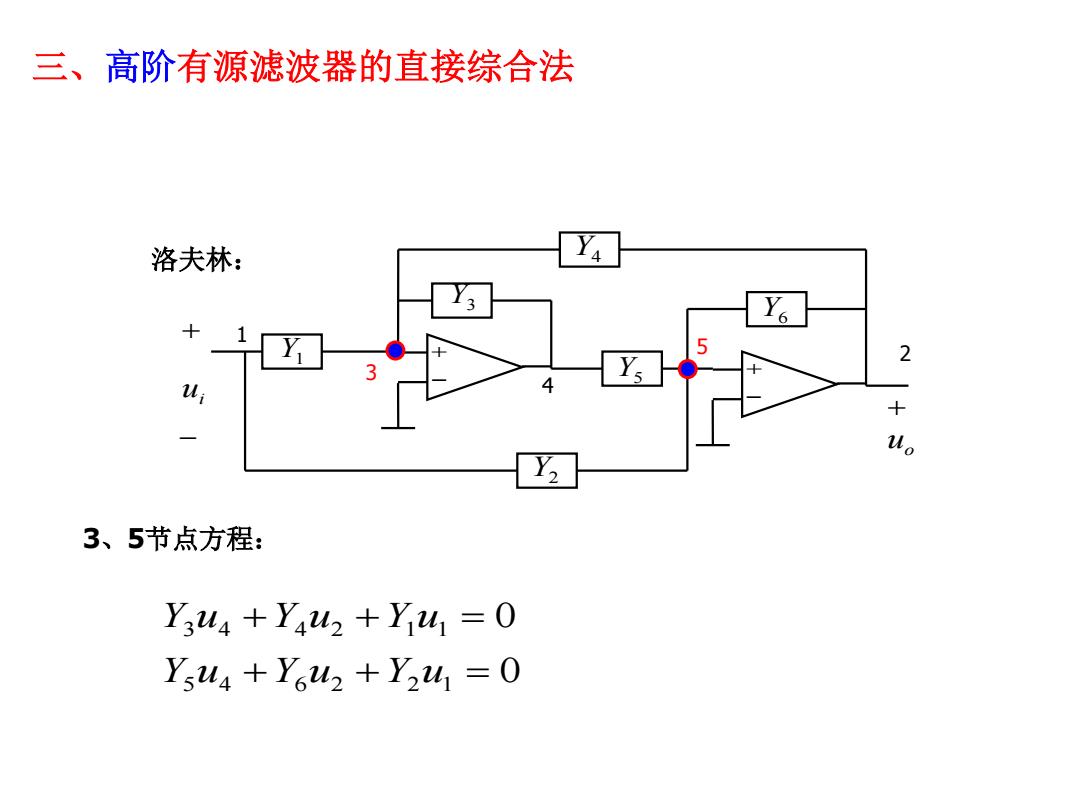
三、高阶有源滤波器的直接综合法 洛夫林： 13 2 3、5节点方程： Y3u4+Y4u2+Y41=0 Y5u4+Y6u2+Y241=0

三、高阶有源滤波器的直接综合法 洛夫林： 0 0 5 4 6 2 2 1 3 4 4 2 1 1       Y u Y u Y u Y u Y u Y u 3、5节点方程： 1 3 2 Y6 ui uo        4 5 Y1 Y3 Y2 Y5 Y4

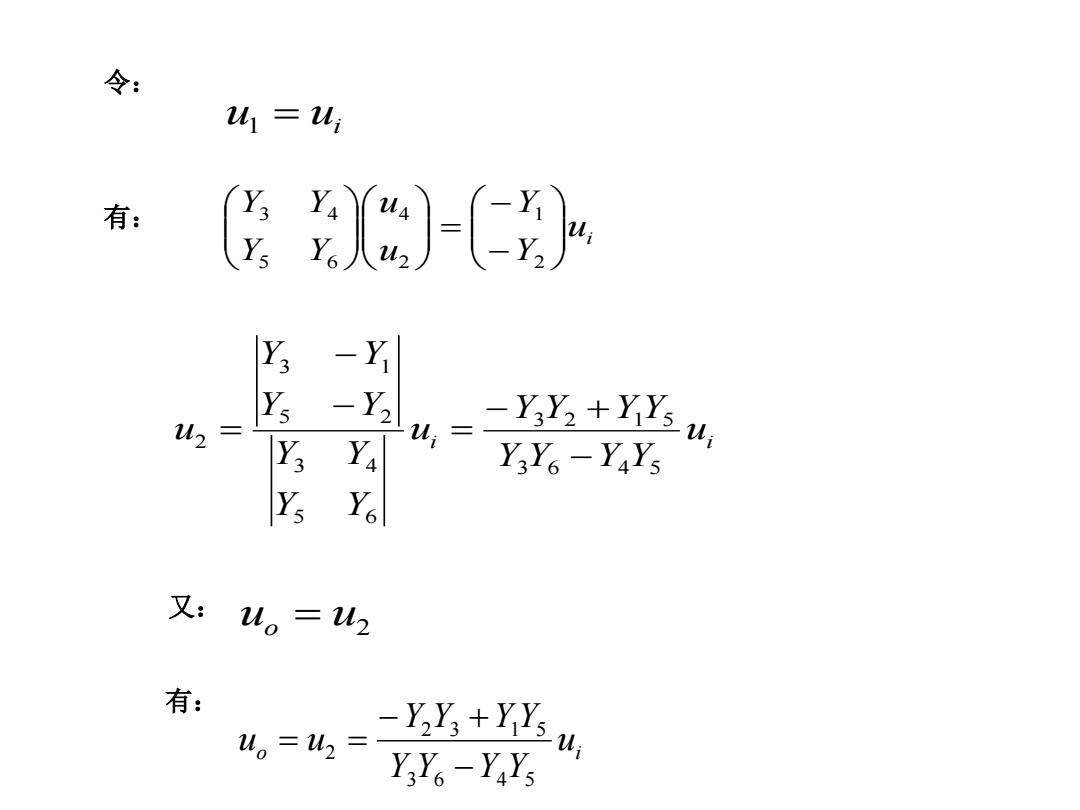
令： u ui 有： a-( Y 2= -Y2 -Yy+Yys u Ya Y3Y6-Y4Ys Ys Ys 又： L。=2 有： M。=u2= -YY+YY-u Y3Y6-YaYs

i ui Y Y Y Y Y Y YY u Y Y Y Y Y Y Y Y u 3 6 4 5 3 2 1 5 5 6 3 4 5 2 3 1 2        u1  ui 令： ui Y Y u u Y Y Y Y                           2 1 2 4 5 6 有： 3 4 uo  u2 又： o ui Y Y Y Y Y Y YY u u 3 6 4 5 2 3 1 5 2      有：

有： T(S)= %= YYs-YY Y3Y6-YaY5 令： Y3=Y=1 归一化 有： T(s)= Y-Y Y。-Y4 设转移函数为： T(S)= W(S) ams"+am=is+.+as+ao D(S)s”+bn-1s”-1+.+bS+b。 m≤n 引入一个多项式QS),其所有根均为负实数，无重根。 有： Q(s)=Π(s+o,) Z≥n-1 i=I

6 4 1 2 ( ) Y Y Y Y T s    Y3  Y5 1 有： m  n 令： 1 0 1 1 1 0 1 1 ... ... ( ) ( ) ( ) s b s b s b a s a s a s a D s N s T s n n n m m m m               有： 3 6 4 5 1 5 2 3 ( ) Y Y Y Y YY Y Y u u T s i o     归一化 设转移函数为： 引入一个多项式Q(s)，其所有根均为负实数，无重根。    l i i Q s s 1 有： ( ) (  ) l  n1

有： T(S)= N(s)/(s) D(s)/0(s) 由： W(s)/2(s)=Y-Y, D(S)/Q(S)=Y6-Y4 由于Q(s)最低可能的幂次较D(S)低一次，故多项式sQ(s) 的最低可能幂次与D(s)同次。同时，注意到Q(S)的全部 根为不同的负实根，因此，D(s)/sQ(s)一般可展开为以 下部分公式： =K:++≥，)(K++z。） se(s) 式中o,及各系数K均为正实常数

6 4 1 2 ( )/ ( ) ( )/ ( ) D s Q s Y Y N s Q s Y Y     有： ( ) ( ) ( ) ( ) 0 0                   i i i i i i s K s K K s K s K K s Q s D s   由： ( )/ ( ) ( )/ ( ) ( ) D s Q s N s Q s T s  由于Q(s)最低可能的幂次较D(s)低一次，故多项式sQ(s) 的最低可能幂次与D(s)同次。同时，注意到Q(s)的全部 根为不同的负实根，因此，D(s)/sQ(s)一般可展开为以 下部分公式： 式中  i 及各系数 K均为正实常数