
Xidian Univ 最短路与Bellman方程 ■假定所有不包括节点1的环具有非负的长度,用D表示从节 点到达目的节点1的最短路径长度。根据前面的讨论,当 B-F算法结束时,有 D,=min[d,+D,]对所有i≠1 (5-6) D=0 该式称为Bellman方程。它表明从节点到达目的节点1的 最短路径长度,等于到达该路径上第一个节点的链路长度, 加上该节点到达目的节点1的最短路径长度。从该方程出 发,只要所有不包括1的环具有正的长度(而不是0长度) 的情况下,我们就可以很容易地找到最短路径(而不是最 短路径长度)。 Broadband Wireless Communications Laboratory,Xidian University 16
Broadband Wireless Communications Laboratory, Xidian University 16 BWC Xidian Univ. ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈~ ≈ ~ ≈ 最短路与Bellman方程 假定所有不包括节点1的环具有非负的长度,用Di表示从节 点i到达目的节点1的最短路径长度。根据前面的讨论,当 B-F算法结束时,有 (5-6) 该式称为Bellman方程 。它表明从节点i到达目的节点1的 最短路径长度,等于i到达该路径上第一个节点的链路长度, 加上该节点到达目的节点1的最短路径长度。从该方程出 发,只要所有不包括1的环具有正的长度(而不是0长度) 的情况下,我们就可以很容易地找到最短路径(而不是最 短路径长度)。 min[ ] 1 i ij j j D dD i =+ ≠ 对所有 0 D1 =
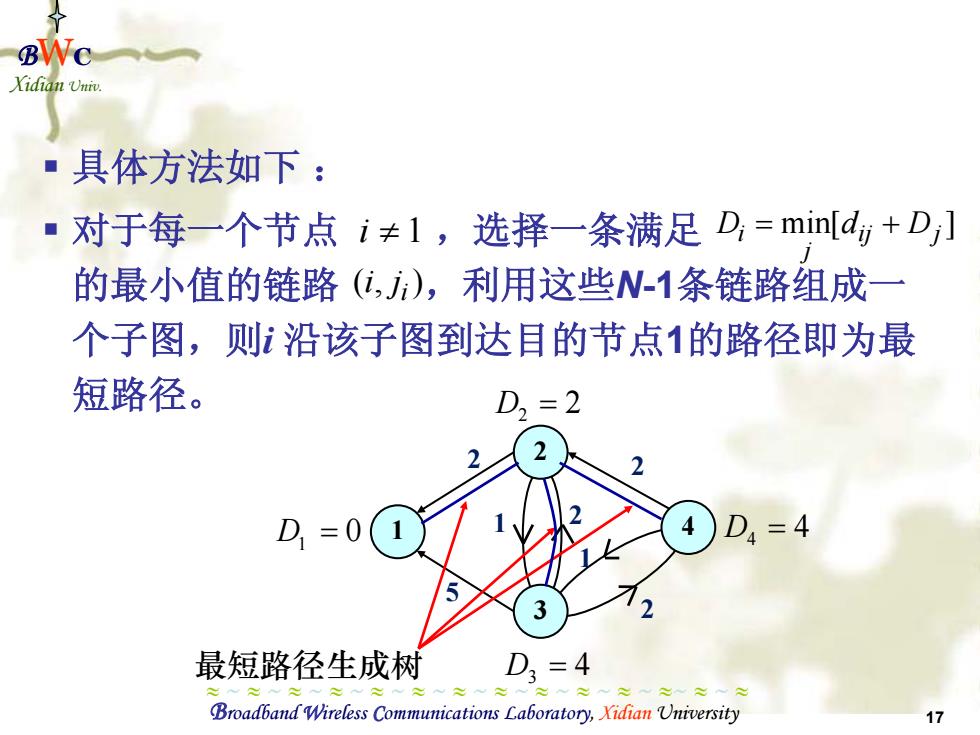
Xidian Univ ■具体方法如下: ·对于每一个节点i≠1,选择一条满足D=min[d,+D] 的最小值的链路(,J),利用这些N-1条链路组成一 个子图,则沿该子图到达目的节点1的路径即为最 短路径。 D2=2 2 D=0 =4 最短路径生成树 D3=4 Broadband Wireless Communications Laboratory,Xidian University 17
Broadband Wireless Communications Laboratory, Xidian University 17 BWC Xidian Univ. ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈ ~ ≈~ ≈ ~ ≈ 具体方法如下 : 对于每一个节点 ,选择一条满足 的最小值的链路 ,利用这些N-1条链路组成一 个子图,则i 沿该子图到达目的节点1的路径即为最 短路径。 i ≠ 1 min[ ] ij j j Di = d + D ( , )i i j 1 2 3 4 2 1 5 2 2 2 1 1 D = 0 2 D = 2 3 D = 4 4 D = 4 最短路径生成树