
2.物种数S和组分数K说明 (3)一个系统的物种数可以随着考虑问题的出发点不同而不同,但在平衡系统中组分数是确定的。例:NaCI-H,O系统1. NaCl, H,O: S-2, R=0, R=0, K-22.NaCI不饱和水溶液:Nat, Cl-, H,O : S=3R=0, R=1: [Nat]=[CI-]K= 3- 1=2
说明(3) 一个系统的物种数可以随着考虑问题的出 发点不同而不同,但在平衡系统中组分数是确定的。 例: NaCl-H2O系统 1. NaCl,H2O: S=2, R=0, R ’=0, K=2 2. 物种数S和组分数K 2. NaCl不饱和水溶液: Na+ , Cl-, H2O : S=3, R=0, R ’=1: [Na+ ]=[Cl-], K= 3– 1=2

2.物种数S和组分数K3.NaCI饱和水溶液,有NaCl(s)存在NaCl(s), Nat, CI-, H,O : S-4R=l: NaCl(s) <> Nat+ CI-R=1: [Nat]-[CI-],K= 4 - 1- 1=24. NaCl(s), Nat, Cl-, H,O ,H+ , OH-:S-6,R=2: NaCl(s) Nat+ CI-, H,O ≤H+ + OH-R=2: [Na+]=[CI-], [H+]=[OH-],电中性 [Na↑]+[H+]-[CI-]+[OH-],K-6-2-2=2
4. NaCl(s), Na+ , Cl-, H2O ,H+ , OH-: S=6, R=2: NaCl(s) Na++ Cl-, H2O H+ + OH-, R ’=2: [Na+ ]=[Cl-], [H+ ]=[OH-], 电中性 [Na+ ]+[H+ ]=[Cl-]+[OH-], K=6– 2–2=2 2. 物种数S和组分数K 3. NaCl饱和水溶液,有NaCl(s)存在 NaCl(s), Na+ , Cl-, H2O : S=4, R=1: NaCl(s) Na++ Cl-, R ’=1: [Na+ ]=[Cl-], K= 4 – 1– 1=2

3. 自由度f在不引起旧相消失和新相形成的前提下,能够在一定范围内独立变动的强度性质称作系统的自由度。即能确立系统状态的独立变量。如Tp,C例:①一杯水和一桶水:T,p,f-2,状态相同,不用确定系统的大小;T, p, c, f-3② NaCI(sln):T,p,f-2(浓度确定c=f(T))③NaCI(饱和):④H,O()-H,O(g)共存系统:f-1。因T,p中只有一个独立变量p=f(T)
3. 自由度f 例: ①一杯水和一桶水: 在不引起旧相消失和新相形成的前提下,能够在一定 范围内独立变动的强度性质称作系统的自由度。即能确立 系统状态的独立变量。如T, p, c T, p, f=2,状态相同,不用确定系统的大小; T, p, c, f=3 T, p, f=2(浓度确定c=f (T)) f=1。因T, p中只有一个独立变量 p=f (T) 。 ② NaCl(sln): ③ NaCl(饱和): ④ H2O(l)-H2O(g)共存系统:
二、相律相律联系K,Φ,f及影响物质性质的外界因素之间关系的规律:f-K-Φ+2相律的推导(Gibbs):设一相平衡系统:该系统有K个组分,Φ个相。在Tp恒定的条件下,有x如下表:β@α1xi(β)xi(α)xi(@)2x2(β)x2(Φ)x2(α)·.....kXk(β)Xk(α)Xk()
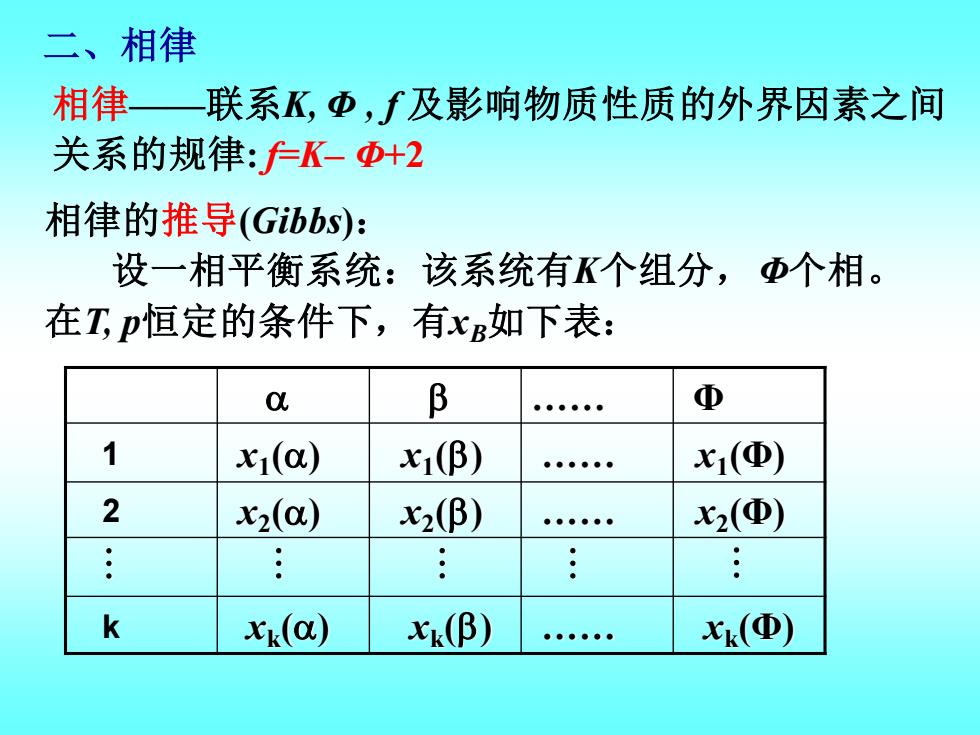
二、相律 相律——联系K, Φ , f 及影响物质性质的外界因素之间 关系的规律: f=K– Φ+2 . Φ 1 2 k 相律的推导(Gibbs): 设一相平衡系统:该系统有K个组分,Φ个相。 在T, p恒定的条件下,有xB如下表: x1 () x2 () xk () x1 () x2 () xk () . . . x1 (Φ) x2 (Φ) xk (Φ)

推导:该平衡系统有K个组分,Φ个相每一相中有(K-1)个浓度,共有Φ个相,除了T,p外还必须指定ΦK-1)个浓度根据相平衡条件,每个组分在各相中的化学势相等: u(α)= μ;(β)=.… u() 则每个组分有(Φ-1)个等式,K个组分则共有K(Φ-1)个等式。: f= Φ(K-1) + 2 -K(Φ-1)= K@-Φ + 2 - KΦ+Kf=K-Φ+2
推导:该平衡系统有K个组分, Φ个相 每一相中有(K–1)个浓度,共有Φ个相,除了T,p外 还必须指定Φ(K–1)个浓度。 f = Φ(K–1) + 2 f = K – Φ + 2 根据相平衡条件,每个组分在各相中的化学势相 等: i () = i () = . i (Φ) 则每个组分有(Φ–1) 个等式,K个组分则共有K(Φ–1)个等式。 – K(Φ–1) = KΦ–Φ + 2 – KΦ+K