
第10章数字信号最佳接收 若rmweok-jas0enpo-aof 则判为发送码元是();若 rweIt0-sj≥oemt0-sofa 侧则判为发送码元是(t)。 将上两式的两端分别取对数,得到若 见hAfo-sofh>a,-s边 则判为发送码元是();反之则判为发送码元是s1()。由于已 经假设两个码元的能量相同,即 ["si(di="si(Odi 16
16 第10章 数字信号最佳接收 若 则判为发送码元是s0 (t);若 则判为发送码元是s1 (t)。 将上两式的两端分别取对数,得到若 则判为发送码元是s0 (t);反之则判为发送码元是s1 (t)。由于已 经假设两个码元的能量相同,即 − − − − Ts Ts r t s t dt n r t s t dt P n P 0 2 0 0 2 0 1 0 ( ) ( ) 1 ( ) ( ) (0)exp 1 (1)exp − − − − Ts Ts r t s t dt n r t s t dt P n P 0 2 0 0 2 0 1 0 ( ) ( ) 1 ( ) ( ) (0)exp 1 (1)exp + − + − Ts Ts r t s t dt P r t s t dt n P n 0 0 2 0 0 2 0 1 ( ) ( ) (0) 1 ( ) ( ) ln (1) 1 ln = Ts Ts s t dt s t dt 0 2 1 0 2 0 ( ) ( )

第10章数字信号最佳接收 上式简化为:若 所+r0s,dt<形+0,0dt 式中 m。=2hP0) 则判为发送码元是(①);反之,则判为发送码元是s1() ·最佳接收机原理方框图: 积分器 (t) So(t) 比较判决 积分器 S1(t) W 17
17 第10章 数字信号最佳接收 上式简化为:若 式中 则判为发送码元是s0 (t);反之,则判为发送码元是s1 (t) ◼ 最佳接收机原理方框图: + + Ts Ts o W r t s t dt W r t s t dt 0 1 1 0 0 ( ) ( ) ( ) ( ) ln (0) 2 0 0 P n W = ln (1) 2 0 1 P n W = S1 (t) W1 r(t) S0 (t) W0 t = Ts 比较判决 积分器 积分器
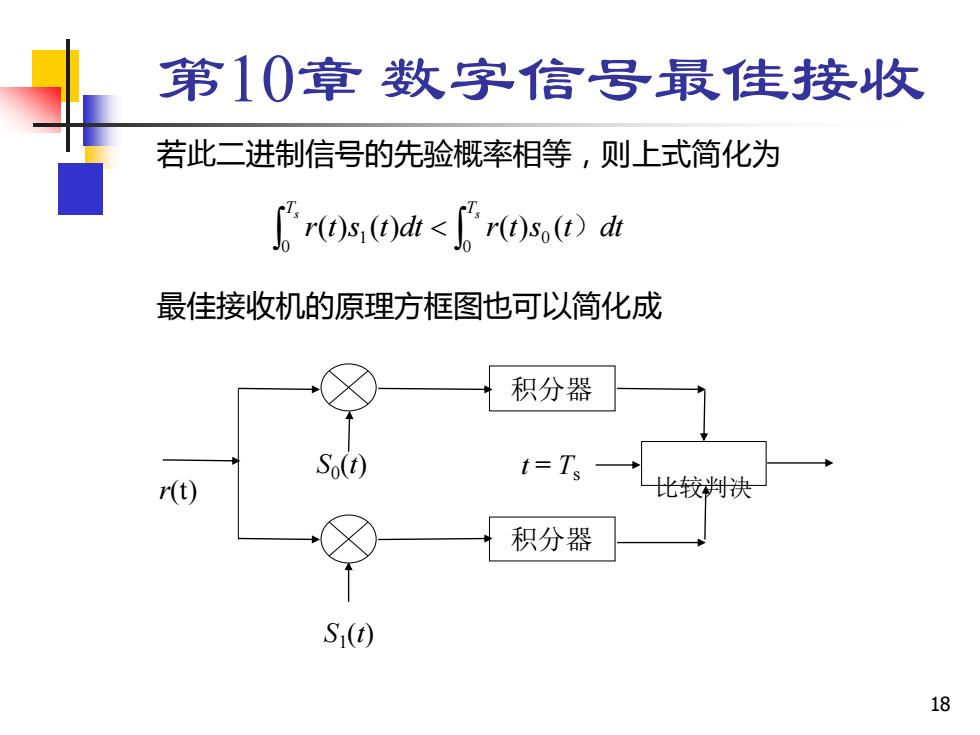
第10章数字信号最佳接收 若此二进制信号的先验慨率相等,则上式简化为 ()s,(d<rs d 最佳接收机的原理方框图也可以简化成 积分器 S() t=Ts r() 比较判决 积分器 S(t) 18
18 r(t) S0 (t) S1 (t) 积分器 积分器 比较判决 t = Ts 第10章 数字信号最佳接收 若此二进制信号的先验概率相等,则上式简化为 最佳接收机的原理方框图也可以简化成 Ts Ts r t s t dt r t s t dt 0 0 1 0 ( ) ( ) ( ) ( )
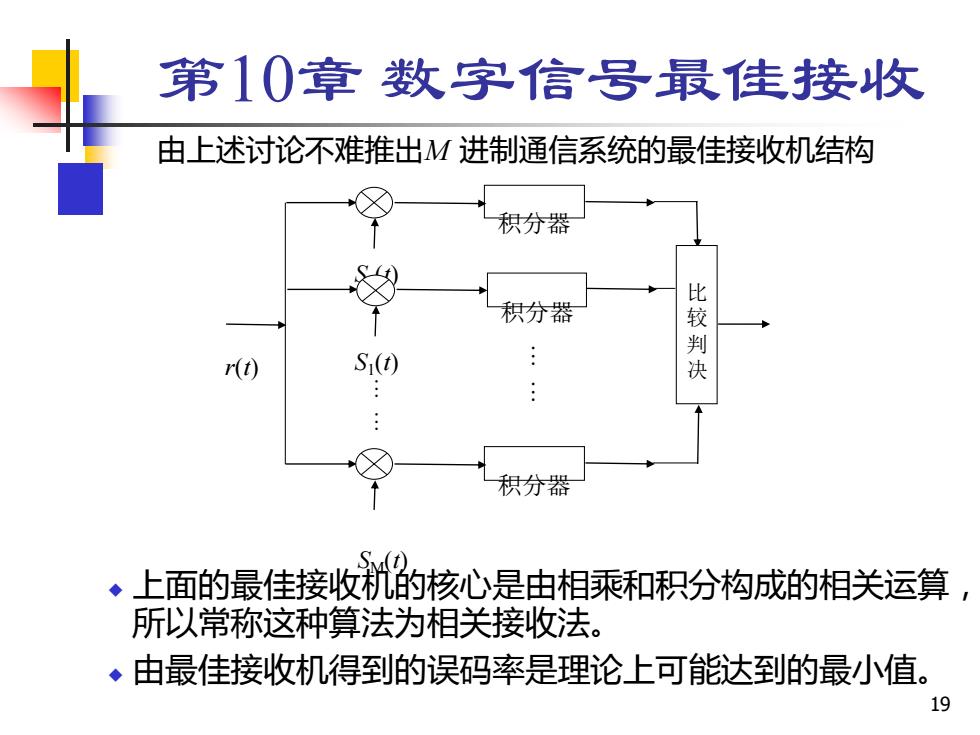
第10章数字信号最佳接收 由上述讨论不难推出M进制通信系统的最佳接收机结构 积分器 积分器 比较判 r(t) S(t 积分器 SM(t) ◆上面的最佳接收机的核心是由相乘和积分构成的相关运算, 所以常称这种算法为相关接收法。 ◆由最佳接收机得到的误码率是理论上可能达到的最小值。 19
19 第10章 数字信号最佳接收 由上述讨论不难推出M 进制通信系统的最佳接收机结构 ◆ 上面的最佳接收机的核心是由相乘和积分构成的相关运算, 所以常称这种算法为相关接收法。 ◆ 由最佳接收机得到的误码率是理论上可能达到的最小值。 积分器 r(t) SM(t) S0 (t) S1 (t) 比 较 判 决 积分器 积分器

第10章数字信号最佳接收 10.4确知数字信号最佳接收的误码率 ·总误码率 在最佳接收机中,若 %h+ft0-ofa>%ho-sofa 则判为发送码元是(t)。因此,在发送码元为S1()时, 若上式成立,则将发生错误判决。所以若将(t)=S() +(t)代入上式,则上式成立的概率就是在发送码元 “1的条件下收到“0的概率,即发生错误的条件概 率P(0/1)。此条件概率的计算结果(计算结果见附 录G)为: 20
20 第10章 数字信号最佳接收 ⚫ 10.4 确知数字信号最佳接收的误码率 ◼ 总误码率 在最佳接收机中,若 则判为发送码元是s0 (t)。因此,在发送码元为s1 (t)时, 若上式成立,则将发生错误判决。所以若将r(t) = s1 (t) + n(t)代入上式,则上式成立的概率就是在发送码元 “1”的条件下收到“0”的概率,即发生错误的条件概 率P(0 / 1)。此条件概率的计算结果(计算结果见附 录G)为: + − + − Ts Ts r t s t dt P r t s t dt n P n 0 0 2 0 0 2 0 1 ( ) ( ) (0) 1 ( ) ( ) ln (1) 1 ln