
新莲火学 Xinjiang University 电气工程学院运动控制系统 异步电动机的三相数学模型 转矩方程 T。=-n,Ln【(i4i。+ig6+icic)sin0+(i4i6+ig。+icia)sin(0+l20) +(i4i。+ig。+ici,)sin(0-120)] 运动方程 J do n,dt =Te-Tn do 转角方程 dt
异步电动机的三相数学模型 转矩方程 ( )sin( 120 ) ( )sin ( )sin( 120 ) + + + − = − + + + + + + A c B a C b e p m s A a B b C c A b B c C a i i i i i i T n L i i i i i i i i i i i i 运动方程 e L p T T dt d n J = − 转角方程 = dt d

亲题火学 电气工程学院-运动控制系统 Xinjiang University 异步电动机三相原始模型的性质 定转子间相对运动 三相绕组间 夹角0不断变化 互感矩阵为 的交又耦合 非线性变参数矩阵 非线性的 定子和 非线性 非线性 基本因素: 转子 旋转电动势 强耦合性 变参数 电磁转矩 的耦合 都包含变量 之间的乘积 磁链方程 转矩方程 电压方程
异步电动机三相原始模型的性质 非线性 变参数 非线性的 基本因素: 旋转电动势 电磁转矩 都包含变量 之间的乘积 定转子间相对运动 夹角不断变化 互感矩阵为 非线性变参数矩阵 非线性 强耦合性 磁链方程 转矩方程 电压方程 定子和 转子 的耦合 三相绕组间 的交叉耦合
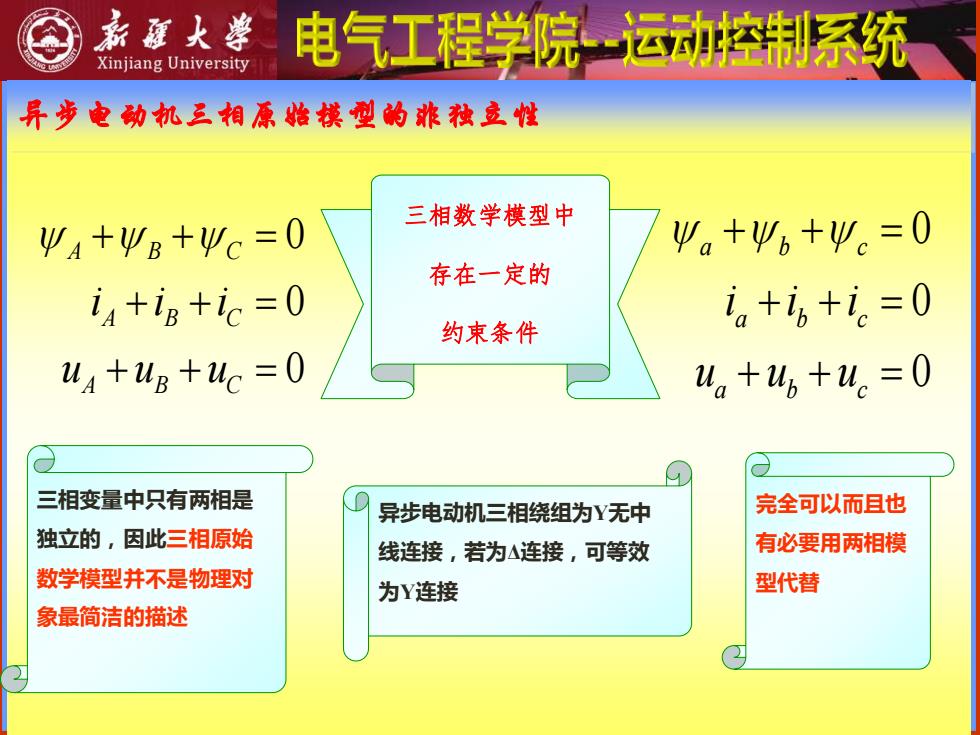
新庭火学 电气工程学院运动控制系统 Xinjiang University 异步电动机三相原始模型的旅秋立性 三相数学模型中 94+ΨB+Ψc=0 9。+必。+以。=0 存在一定的 ia +ig +ic =0 i。+i6+i。=0 约束条件 ua +up +uc 0 。+u,+u。=0 三相变量中只有两相是 异步电动机三相绕组为Y无中 完全可以而目也 独立的,因此三相原始 线连接,若为△连接,可等效 有必要用两相模 数学模型并不是物理对 为Y连接 型代替 象最简洁的描述
异步电动机三相原始模型的非独立性 三相数学模型中 存在一定的 约束条件 0 0 0 A B C A B C A B C iii uuu + + = + + = + + = 0 0 0 a b c a b c a b c i i i u u u + + = + + = + + = 异步电动机三相绕组为Y无中 线连接,若为Δ连接,可等效 为Y连接 三相变量中只有两相是 独立的,因此三相原始 数学模型并不是物理对 象最简洁的描述 完全可以而且也 有必要用两相模 型代替
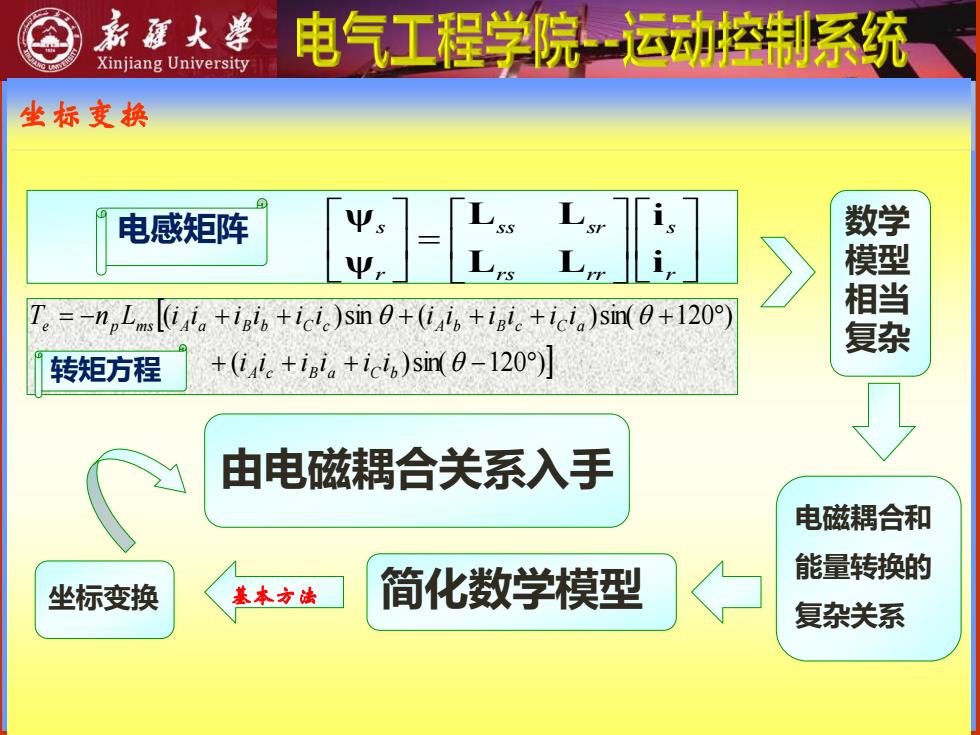
系庭大学 电气工程学院运动控制系统 Xinjiang University 坐标变换 电感矩阵 Ψs nLm(ii+igin +icic)sin +(iai +igi +icia)sin(0+120) 转矩方程 +(iie+ini +ici)sin0120 由电磁耦合关系入手 电磁耦合和 简化数学模型 能量转换的 坐标变换 基本方法 复杂关系
坐标变换 ( )sin( 120 ) ( )sin ( )sin( 120 ) + + + − = − + + + + + + A c B a C b e p m s A a B b C c A b B c C a i i i i i i T n L i i i i i i i i i i i i 转矩方程 s s ss sr r r rs rr = ψ L L i ψ L L i 电感矩阵 数学 模型 相当 复杂 电磁耦合和 能量转换的 简化数学模型 复杂关系 坐标变换 基本方法 由电磁耦合关系入手
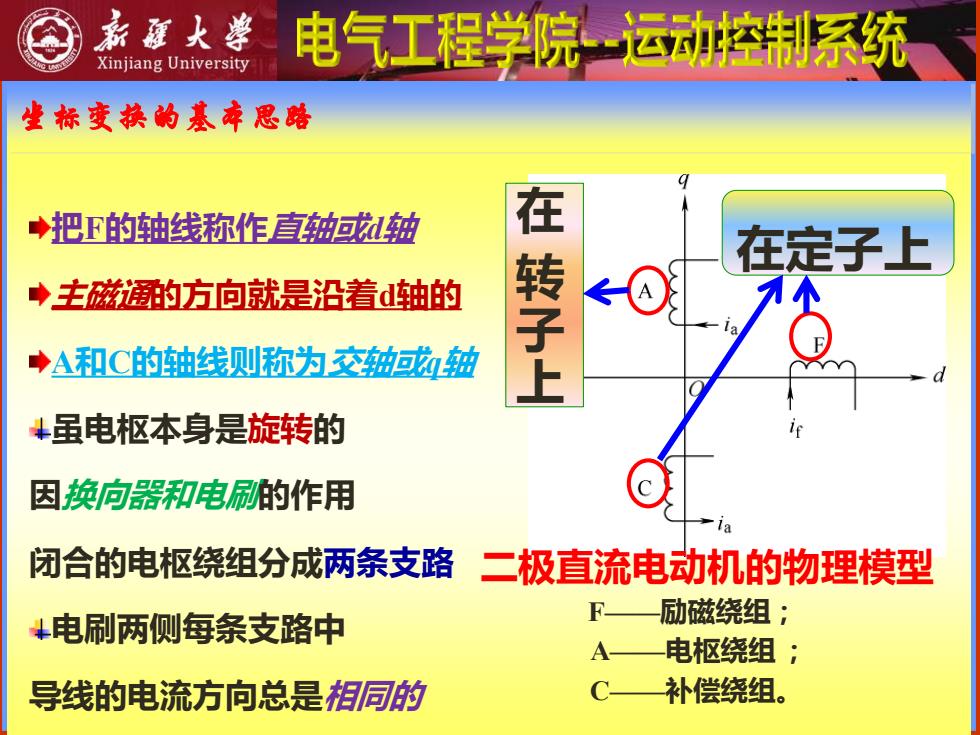
新庭火学 电气工程学院运动控制系统 Xinjiang University 坐标变换的基碎思路 ◆把F的轴线称作直轴回或u抽 在定子上 ◆主磁的方向就是沿着d轴的 ◆A和C的轴线则称为交轴或轴 在转子上 虽电枢本身是旋转的 因换向器和电刷的作用 闭合的电枢绕组分成两条支路 二极直流电动机的物理模型 F 电刷两侧每条支路中 励磁绕组; A—电枢绕组: 导线的电流方向总是相同的 C 补偿绕组
坐标变换的基本思路 二极直流电动机的物理模型 F——励磁绕组; A——电枢绕组 ; C——补偿绕组。 在 转 子 上 在定子上 把F的轴线称作直轴或d轴 主磁通的方向就是沿着d轴的 A和C的轴线则称为交轴或q轴 虽电枢本身是旋转的 因换向器和电刷的作用 闭合的电枢绕组分成两条支路 电刷两侧每条支路中 导线的电流方向总是相同的