收象 Nanjing University Basic Principle 02=c2g2+m2c4h2 o=cq Kouanba Kouanba.y 0=mc2h1=0p 0=0 wave vector wave vector Dispersion of light in free space and perfect metal Dielectrie Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
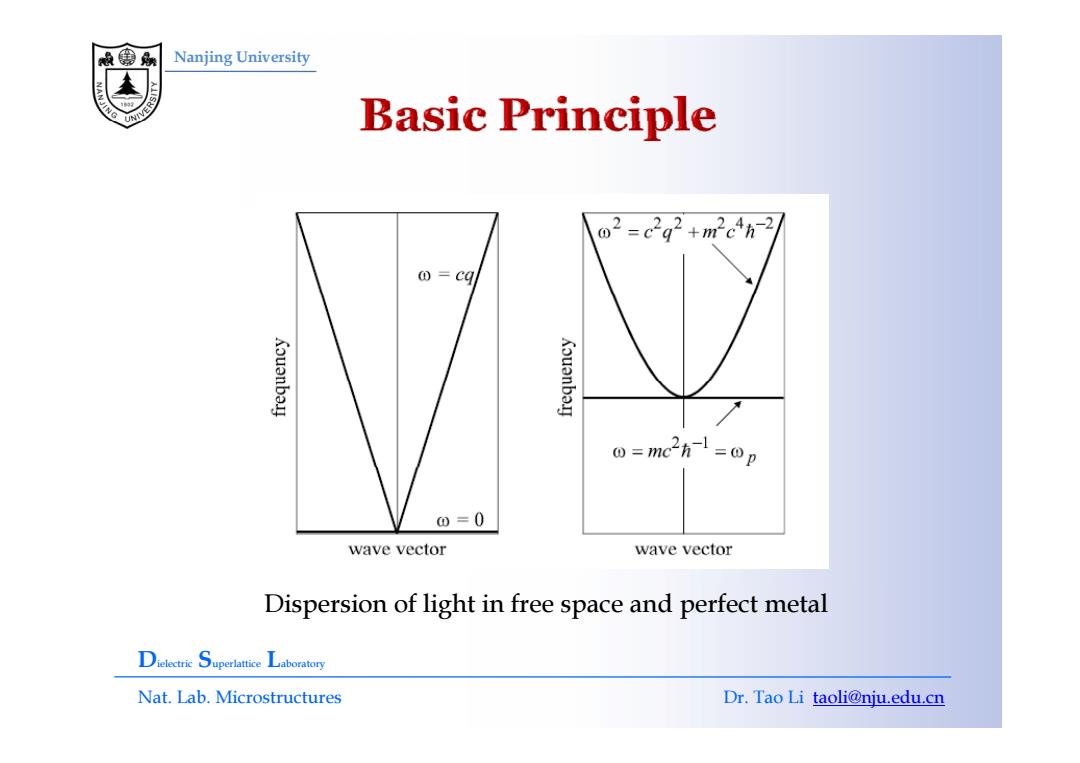
Nanjing University Dispersion of light in free space and perfect metal Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn

Nanjing University Basic Principle Considering the bound electron with resonance frequency@o e.g.geometric boundary,interband transition,or other forces... It is more popular case in real metallic system mx+myx+moox=-eE oj c(0)=I+o-@-iy@ Lorentz Model Dielectric Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
Nanjing University Considering the bound electron with resonance frequencyω0 e.g g y, , . geometric boundary, interband transition, or other forces… It is more popular case in real metallic system mm m e 0 && & x x xE + γ + =− ω 2 2 2 0 () 1 P i ω ε ω ω ω γω = + − − Lorentz Model Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn

Nanjing University Basic Principle Optical property of medium refractive index n,extinction coefficient K 61=n2-K2,62=2nK and n= 方a+1G+月 K-- 2(←6+(6+)2)2 n and &are not independent variable s Dielectric Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
Nanjing University Op pp y tical property of medium refractive index n, extinction coefficient κ 2 2 2 1 2 1 1 n n , and ε = − = κε κ 1 1 2 2 2 2 1 12 1 1 1 ( ( )) 2 n = ++ ε εε 1 1 2 2 2 2 1 12 1 ( ( )). 2 κ ε εε = −+ + r n and are not independent variable s % ε% Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn
Nanjing University Basic Principle Considering the plasmon frequency &(o)=1-0 ⊙ 01 i=ve, wave vector >op,n is real =p 0=0p,n=0 o<op,n is imaginary Plasma frequency 1.0 Optical reflectivity 0.8 0.6 0.4 (n+1)2+K2 0.2 0.0 0 /p Dieletrie Superlantice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
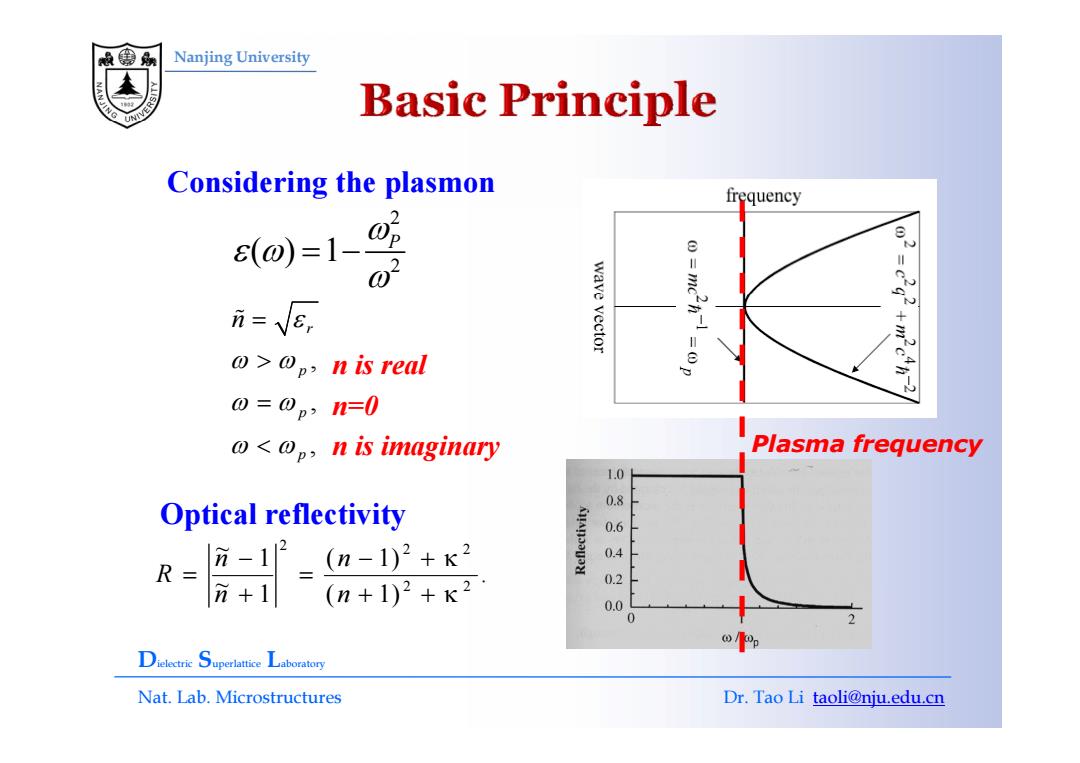
Nanjing University Considering the plasmon 2 2 () 1 ωP ε ω ω = − , r p n ε ω ω = > % n is real , , p p ω ω ω ω = < Plasma frequency n=0 n is imaginary Optical reflectivity 1 ( 1) ~ 2 2 2 + κ . ( 1) ( 1) 1 ~ 1 2 2 + + κ − + κ = + − = n n n n R Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn

Nanjing University Outline Concepts Basic principles Surface Plasmon SPP at flat metal surfaces Optical excitation of SPP Localized Surface plasmon (LSP) Application of SPP Metamaterial Summary Dielectric Superlatice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn
Nanjing University y Concepts y Basic principles y Surface Plasmon Surface Plasmon SPP at flat metal surfaces Optical excitation of SPP Optical excitation of SPP Localized Surface plasmon (LSP) Application of SPP y Metamaterial y Summary Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn