高等教育出版社：《物理学教程》教材电子教案（PPT课件，马文蔚第二版）第十二章 电磁感应、电磁场和电磁波 12-5 位移电流 电磁场基本方程的积分形式

*12-5位移电流电磁场基本方程的积分形式 物理学教程 (第二版) 麦克斯韦(1831-1879) 英国物理学家.经典电磁理 论的奠基人，气体动理论创 始人之一.他提出了有旋场 和位移电流的概念，建立了 经典电磁理论，并预言了以 光速传播的电磁波的存在. 在气体动理论方面，他还提 出了气体分子按速率分布的 统计规律. 第十二章电磁感应电滋场和电磁波

第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 5 位移电流 电磁场基本方程的积分形式 （第二版） 麦克斯韦（1831-1879） 英国物理学家 . 经典电磁理 论的奠基人 , 气体动理论创 始人之一 . 他提出了有旋场 和位移电流的概念 , 建立了 经典电磁理论 , 并预言了以 光速传播的电磁波的存在 . 在气体动理论方面 , 他还提 出了气体分子按速率分布的 统计规律

*12-5位移电流电磁场基本方程的积分形式 物理学教程 (第二版) 1865年麦克斯韦在总结前人工作的基础上，提出 完整的电磁场理论，他的主要贡献是提出了“有旋电 场”和“位移电流”两个假设，从而预言了电磁波的 存在，并计算出电磁波的速度（即光速）. C Eomo (真空中) 1888年赫兹的实验证实了他的预言，麦克斯韦理 论奠定了经典动力学的基础，为无线电技术和现代电 子通讯技术发展开辟了广阔前景. 第十二章电磁感应电磁场和电磁波

第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 5 位移电流 电磁场基本方程的积分形式 （第二版） 1865 年麦克斯韦在总结前人工作的基础上，提出 完整的电磁场理论， 他的主要贡献是提出了“有旋电 场”和“位移电流” 两个假设，从而预言了电磁波的 存在，并计算出电磁波的速度（即光速）. 1888 年赫兹的实验证实了他的预言, 麦克斯韦理 论奠定了经典动力学的基础，为无线电技术和现代电 子通讯技术发展开辟了广阔前景. 0 0 1   c = ( 真空中 )

*12-5位移电流电磁场基本方程的积分形式 物理学教程 (第二版) 位移电流全电流安培环路定理 稳恒磁场中，安培环路定理 fB.d=4∑1=hsjd (以L为边做任意曲面S) S? 5B.d=4jds=4l。 f,B-di=Mos j 此矛盾如何解释？ 第十二章电磁感应电磁场和电磁波

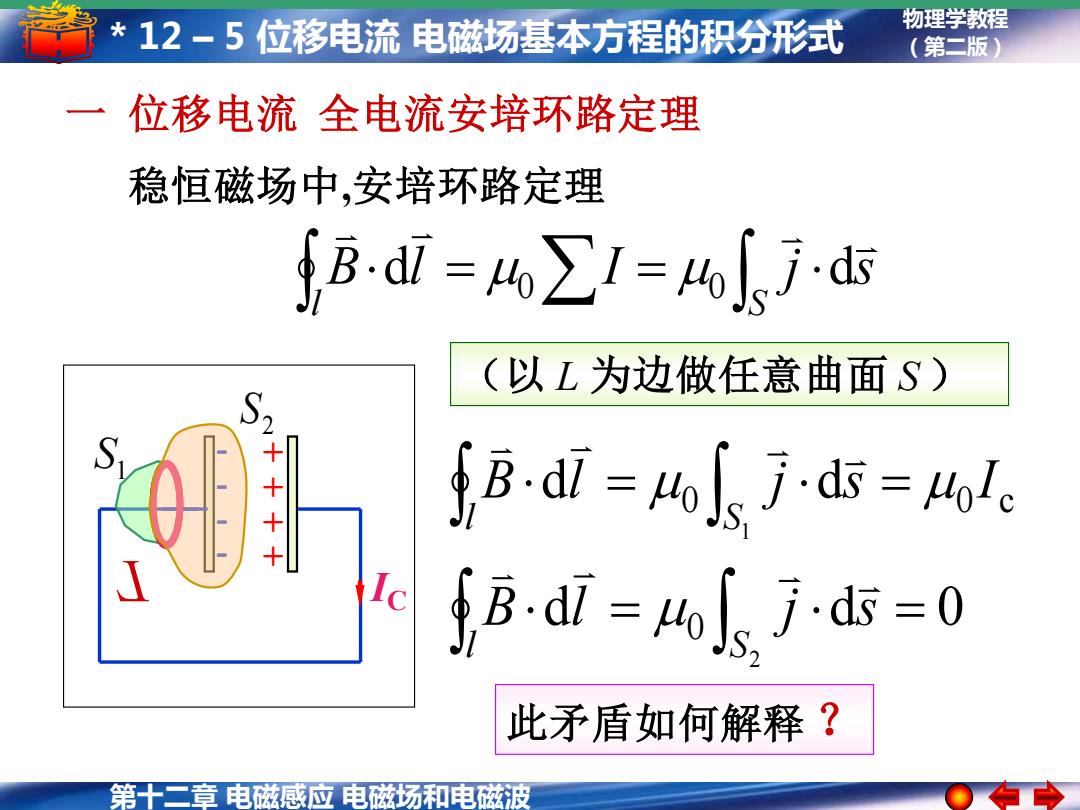
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 5 位移电流 电磁场基本方程的积分形式 （第二版） 一 位移电流 全电流安培环路定理 + + + + - - - - IC （以 L 为边做任意曲面 S ） L 1 S 2 S    =  = 1 0 0 c d d l S B l  j s  I        =  = 2 d d 0 0 l S B l j s      稳恒磁场中,安培环路定理     = =  l S B l I j s     d d 0 0 此矛盾如何解释 ？

*12-5位移电流电磁场基本方程的积分形式 物理学教程 (第二版) dq d(So) do O S dt dt dt jc do E dE 1 do dt 80 dt 60 dt dΦ S do 1 dq dt 6o di 麦克斯韦假设电场中某一点位移电流密度等 于该点电位移矢量对时间的变化率， dE 位移电流密度 ja=80 dt 第十二章电磁感应电磁场和电磁波

第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 5 位移电流 电磁场基本方程的积分形式 （第二版） t S t S t q I d d d d( ) d d c   = = = t j d d c  = 0 E   = 0 d 1 d d d E t t   = e 0 0 d d 1 d d d d S q t t t     = = 麦克斯韦假设 电场中某一点位移电流密度等 于该点电位移矢量对时间的变化率. d 0 d d E j t 位移电流密度 =  + + + + + - - - - - IC d d E t E c j c j − + IC B A

*12-5位移电流电磁场基本方程的积分形式 物理学教程 (第二版) dE 位移电流密度 d dt 移流7，-小i,5- dE ◆ dΦ dt 通过电场中某一截面的位移 电流等于通过该截面电场强度通 量对时间的变化率与。的乘积. 电容器中位移电流I。=I。 回路中全电流连续 全电流 第十一章电滋感应电磁场和电磁波

第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 5 位移电流 电磁场基本方程的积分形式 （第二版） 位移电流 e d d 0 0 d d d d S S d d E I j s S t t    =  =  =   + + + + + - - - - - d I c I 全电流 s c d I = I + I d 0 d d E j t 位移电流密度 =  通过电场中某一截面的位移 电流等于通过该截面电场强度通 量对时间的变化率与 的乘积 . o  电容器中位移电流 d c I = I 回路中全电流连续