
12-2动生电动势和感生电动势 物理学教程 (第二版) 引起磁通量变化的原因 1)稳恒磁场中的导体运动,或者回路面积 变化、取向变化等>动生电动势 2)导体不动,磁场变化→感生电动势 ◆电动势 E-fe.-dr E:非静电的电场强度。 ◆闭合电路的总电动势 -∮Edi E 第十二章电磁感应电磁场和电磁波
第十二章电磁感应 电磁场和电磁波 物理学教程 12 – 2 动生电动势和感生电动势 (第二版) 引起磁通量变化的原因 1)稳恒磁场中的导体运动 , 或者回路面积 变化、取向变化等 动生电动势 2)导体不动,磁场变化 感生电动势 电动势 + - Ek I + − = E l E k d = l E l 闭合电路的总电动势 E k d Ek : 非静电的电场强度

12-2动生电动势和感生电动势 物理学教程 (第二版) 动生电动势 动生电动势的非静电力场来源→洛伦兹力 Fm=(-e)i×B +D十 平衡时Fm=-f。=-eE m -e E=∫.E·dI=n(o×B)dl 设杆长为1E=Bdl=oBl 第十二章电磁感应电磁滋场和电磁波
第十二章电磁感应 电磁场和电磁波 物理学教程 12 – 2 动生电动势和感生电动势 (第二版) + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + v B O P 设杆长为 l 一 动生电动势 动生电动势的非静电力场来源 洛伦兹力 - Fm - - ++ Fe F e B m = (− )v 平衡时 m e Ek F F e = − = − B e F E = − = v m k = OP B l (v ) d = OP E l Ei k d B l Bl l = v = v 0 Ei d p o Ei
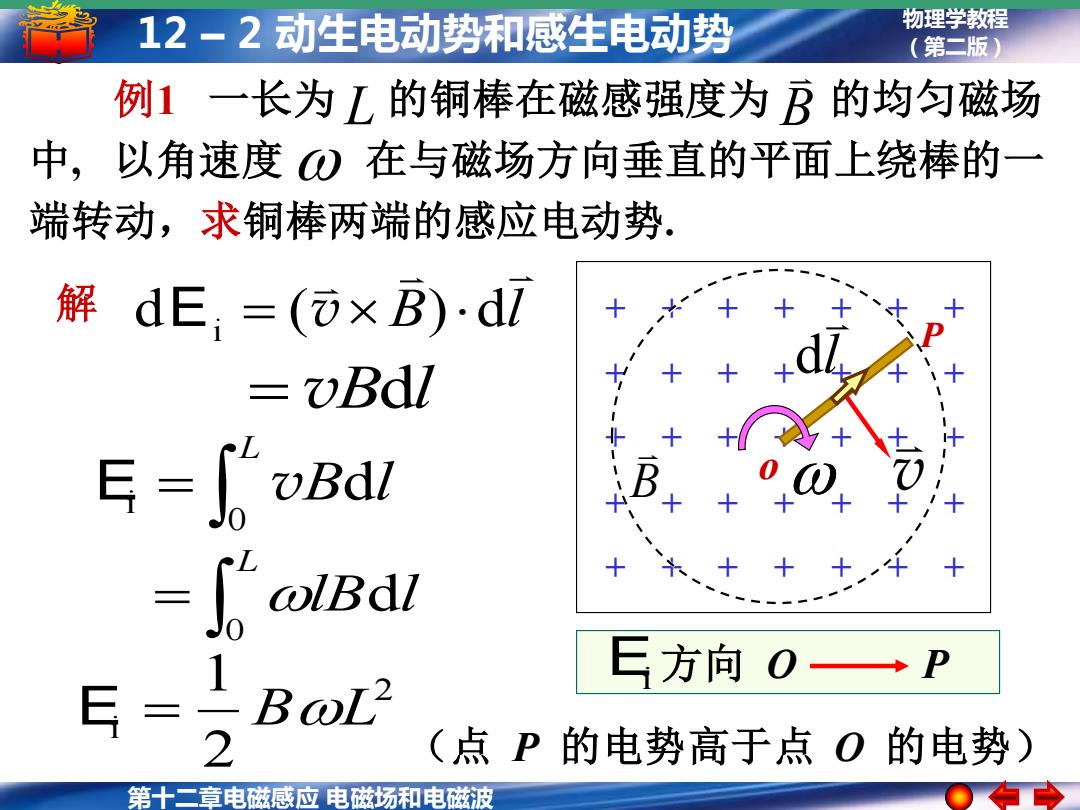
12-2动生电动势和感生电动势 物理学教程 (第二版) 例1一长为「的铜棒在磁感强度为万的均匀磁场 中,以角速度)在与磁场方向垂直的平面上绕棒的一 端转动,求铜棒两端的感应电动势, 解dE:=()×B):dl vBdl E = vBdl alBdl E方向0 E 1 2 (点P的电势高于点O的电势) 第十二章电磁感应电磁场和电磁波
第十二章电磁感应 电磁场和电磁波 物理学教程 12 – 2 动生电动势和感生电动势 (第二版) 解 = vBdl = L lB l 0 d = L B l 0 Ei v d 2 i 2 1 E = BL B l d ( ) d i E = v 例1 一长为 的铜棒在磁感强度为 的均匀磁场 中, 以角速度 在与磁场方向垂直的平面上绕棒的一 端转动,求铜棒两端的感应电动势. L B + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + o P B (点 P 的电势高于点 O 的电势) Ei 方向 O P v l d

12-2动生电动势和感生电动势 物理学教程 (第二版) 例2一导线矩形框的平面与磁感强度为阝的均 匀磁场相垂直.在此矩形框上,有一质量为长为1的 可移动的细导体棒N;矩形框还接有一个电阻R, 其值较之导线的电阻值要大得很多.若开始时,细导 体棒以速度⑦。沿如图所示的矩形框运动,试求棒的 速率随时间变化的函数关系. 解如图建立坐标 棒中E=Blo且由M一W B R 棒所受安培力 B212) F=IBI= R 方向沿Ox轴反向 第十二章电磁感应电磁场和电磁波
第十二章电磁感应 电磁场和电磁波 物理学教程 12 – 2 动生电动势和感生电动势 (第二版) 例2 一导线矩形框的平面与磁感强度为 的均 匀磁场相垂直.在此矩形框上,有一质量为 长为 的 可移动的细导体棒 ; 矩形框还接有一个电阻 , 其值较之导线的电阻值要大得很多. 若开始时, 细导 体棒以速度 沿如图所示的矩形框运动, 试求棒的 速率随时间变化的函数关系. m l B MN R 0 v 解 如图建立坐标 棒所受安培力 R v 2 2 B l F = IBl = 方向沿ox轴反向 F R l B v o x M N 棒中 Ei = Blv 且由 M N I

12-2动生电动势和感生电动势 物理学教程 (第二版) B212) F=IBI= 方向沿Ox轴反向 R 棒的运动方程为 dv B2120 B m dt R 7 则 M 71 mR 计算得棒的速率随时间变化的函数关系为 Voe-(B2P/mR)t 第十二章电磁感应电磁场和电磁波
第十二章电磁感应 电磁场和电磁波 物理学教程 12 – 2 动生电动势和感生电动势 (第二版) R v 2 2 B l F = IBl = 方向沿 ox 轴反向 棒的运动方程为 R v v 2 2 d d B l t m = − 则 = − t t B l 0 2 2 d d v mR v v v0 计算得棒的速率随时间变化的函数关系为 (B l )t 2 2 e mR v v0 − = F R l B v o x M N I