
评价依据:课堂笔记、提问和作业、课外作业和考 试。 四、课程内容 教学内容 作业要求 第一章空间解析几何 自学内容:空间直角坐标系;点的坐标; 两点间距离公式;向量的基本概念;向量 8.1空间直角坐标系 及其运算的坐标表示;直线与直线;直线 8.2向量及线性运算 与平面的位置关系。 83向量的内积与外积 8.4空间直线与平面 课堂作业: 8.5空间曲面与方程 教材思考题、习题 8.6空间曲线及其方程 课外作业: 知识点: 同步辅导书、习题 1.理解空间直角坐标系。 2.理解向量的概念及其表示,掌握向量的运 算(线性运算、数量积、向量积),掌握两个 向量垂直、平行的条件。 3.掌握单位向量、方向余弦、向量的坐标表 达式以及用坐标表达式进行向量运算的方 法。 4.掌握常用平面方程和直线方程及其求法, 能根据平面和直线的相互关系解决有关问 题。 5,理解曲面方程的概念,了解常用二次曲面 的方程及其图形,了解以坐标轴为旋转轴的 旋转曲面及母线平行于坐标轴的柱面方程。 6.了解空间曲线的参数方程和一般方程。 7.了解曲面的交线在坐标平面上的投影。 第二章多元函数徽分法及其应用 自学内容:多元函数的基本概念;隐函数 微分法;微分法在几何上的应用 91多元函数的基本概念
9 评价依据:课堂笔记、提问和作业、课外作业和考 试。 四、课程内容 教学内容 作业要求 第一章 空间解析几何 8.1 空间直角坐标系 8.2 向量及线性运算 8.3 向量的内积与外积 8.4 空间直线与平面 8.5 空间曲面与方程 8.6 空间曲线及其方程 知识点: 1. 理解空间直角坐标系。 2. 理解向量的概念及其表示,掌握向量的运 算(线性运算、数量积、向量积),掌握两个 向量垂直、平行的条件。 3. 掌握单位向量、方向余弦、向量的坐标表 达式以及用坐标表达式进行向量运算的方 法。 4. 掌握常用平面方程和直线方程及其求法, 能根据平面和直线的相互关系解决有关问 题。 5. 理解曲面方程的概念,了解常用二次曲面 的方程及其图形,了解以坐标轴为旋转轴的 旋转曲面及母线平行于坐标轴的柱面方程。 6. 了解空间曲线的参数方程和一般方程。 7. 了解曲面的交线在坐标平面上的投影。 自学内容:空间直角坐标系;点的坐标; 两点间距离公式;向量的基本概念;向量 及其运算的坐标表示;直线与直线;直线 与平面的位置关系。 课堂作业: 教材思考题、习题 课外作业: 同步辅导书、习题 第二章多元函数微分法及其应用 9.1 多元函数的基本概念 自学内容:多元函数的基本概念;隐函数 微分法;微分法在几何上的应用

9.2偏导数 课堂作业: 9.3全微分及其应用 教材思考题、习题 课外作业: 9.4多元复合函数的求导法 同步辅导书、习题 9.5隐函数微分法 9.6微分法在几何上的应用 9.7方向导数与梯度 9.8多元函数的极值 知识点: 1,了解中点的邻域、内点、开集、区域等概 念。 2.理解多元函数的概念,理解二元函数的几 何意义。 3.理解多元函数的极限及连续的概念,了解 有界闭区域上连续函数的性质。 4.理解多元函数的全微分和偏导数的概念, 了解全微分存在的必要条件和充分条件,了 解一阶全微分形式的不变性。 5.了解方向导数与梯度的概念及其计算方 法。 6.掌握复合函数一阶偏导数的求法,会求复 合函数的二阶偏导数。 7.会求隐含数(包括由两个方程组成的方程 组确定的隐含数)的偏导数。 8.了解曲线的切线和法平面及曲面的切平面 与法线,并会求它们的方程。 9.了解多元函数的极值与条件极值的概念, 会求二元函数的极值。了解Lagrange乘数法 求条件极值,会求简单的多元函数的最大值 10
10 9.2 偏导数 9.3 全微分及其应用 9.4 多元复合函数的求导法 9.5 隐函数微分法 9.6 微分法在几何上的应用 9.7 方向导数与梯度 9.8 多元函数的极值 知识点: 1. 了解中点的邻域、内点、开集、区域等概 念。 2. 理解多元函数的概念,理解二元函数的几 何意义。 3. 理解多元函数的极限及连续的概念,了解 有界闭区域上连续函数的性质。 4. 理解多元函数的全微分和偏导数的概念, 了解全微分存在的必要条件和充分条件,了 解一阶全微分形式的不变性。 5. 了解方向导数与梯度的概念及其计算方 法。 6. 掌握复合函数一阶偏导数的求法,会求复 合函数的二阶偏导数。 7. 会求隐含数(包括由两个方程组成的方程 组确定的隐含数)的偏导数。 8. 了解曲线的切线和法平面及曲面的切平面 与法线,并会求它们的方程。 9. 了解多元函数的极值与条件极值的概念, 会求二元函数的极值。了解 Lagrange 乘数法 求条件极值,会求简单的多元函数的最大值 课堂作业: 教材思考题、习题 课外作业: 同步辅导书、习题

和最小值问题的解。 第三章重积分 自学内容:重积分的概念与性质;重积分 的应用:几何应用、物理应用。 10.1二重积分的概念和性质 课堂作业: 10.2二重积分的计算(一) 教材思考题、习题 10.3二重积分的计算(二) 课外作业: 10.4三重积分的计算(一) 同步辅导书、习题 知识点: 1.理解二重积分和三重积分的概念及性质。 2.掌握二重积分的计算方法(直角坐标、极 坐标)。 3.了解三重积分的计算方法(直角坐标)。 4.了解用积分计算重心、转动惯量和引力的 方法。 5,掌握利用二重积分计算曲顶柱体体积的方 法。 6.了解二重积分在物理中的应用 第四章曲线与曲面积分 自学内容:;两类曲线积分的联系;两类 曲面积分的联系;*高斯公式与斯托克斯公 11.1对弧长的曲线积分 式。 11.2对坐标的曲线积分 11.3格林公式及其应用 课堂作业: 11.4对面积的曲面积分 教材思考题、习题 11.5对坐标的曲面积分 课外作业: 11.6高斯公式与斯托克斯公式 同步辅导书、习题 知识点: 1.理解曲线弧长的概念,理解第一类曲线积 分的概念性质,掌握第一类曲线积分的计 算。 2.理解第二类曲线积分的概念,性质,并掌 握其计算。 11
11 和最小值问题的解。 第三章 重积分 10.1 二重积分的概念和性质 10.2 二重积分的计算(一) 10.3 二重积分的计算(二) 10.4 三重积分的计算(一) 知识点: 1. 理解二重积分和三重积分的概念及性质。 2. 掌握二重积分的计算方法(直角坐标、极 坐标)。 3. 了解三重积分的计算方法(直角坐标)。 4. 了解用积分计算重心、转动惯量和引力的 方法。 5. 掌握利用二重积分计算曲顶柱体体积的方 法。 6. 了解二重积分在物理中的应用 自学内容:重积分的概念与性质;重积分 的应用:几何应用、物理应用。 课堂作业: 教材思考题、习题 课外作业: 同步辅导书、习题 第四章 曲线与曲面积分 11.1 对弧长的曲线积分 11.2 对坐标的曲线积分 11.3 格林公式及其应用 11.4 对面积的曲面积分 11.5 对坐标的曲面积分 11.6 高斯公式与斯托克斯公式 知识点: 1. 理解曲线弧长的概念,理解第一类曲线积 分的概念性质,掌握第一类曲线积分的计 算。 2. 理解第二类曲线积分的概念,性质,并掌 握其计算。 自学内容:;两类曲线积分的联系;两类 曲面积分的联系;*高斯公式与斯托克斯公 式。 课堂作业: 教材思考题、习题 课外作业: 同步辅导书、习题

3.了解两类曲线积分的关系。 4.理解曲面面积的概念,理解第一类曲面积 分的概念,性质并掌握其计算。 5.了解有向曲面的概念,理解第二类曲面积 分的概念,性质并掌握其计算。 6.掌握Green公式和Gauss公式,并会利用 它们计算积分。 第五章无穷级数 自学内容:常数项级数的概念,级数的性 质;幂级数的应用(求数项级数的和、近 12.1常数项级数的概念和性质 似计算、欧拉公式);傅立叶级数; 12.2常数项级数的审敛法 12.3幂级数 课堂作业: 12.4函数展开成幂级数 教材思考题、习题 12.5傅里叶级数* 课外作业: 知识点: 同步辅导书、习题 1.理解数项级数收敛、发散及收敛级数和的 概念,掌握级数的基本性质及收敛的必要条 件。 2.掌握几何级数、P-级数和级数收敛与发散 的条件。 3.掌握正项级数收敛性的比较判别法,比值 判别法和根值判别法。 4.了解任意项数的绝对收敛与条件收敛的概 念及关系,掌握交错级数的Leibniz判别法。 5.了解函数项级数的收敛域及和函数的概 念。 6.掌握幂级数的收敛半径,收敛区间的求 法。 7.了解幂级数的连续性、逐项微分和逐项积 分等性质,并能利用这些性质求一些幂级数 的和函数与某些数项级数的和。 8.了解Taylor级数与余项公式,掌握基本初 级函数的Taylor展开。 12
12 3. 了解两类曲线积分的关系。 4. 理解曲面面积的概念,理解第一类曲面积 分的概念,性质并掌握其计算。 5. 了解有向曲面的概念,理解第二类曲面积 分的概念,性质并掌握其计算。 6. 掌握 Green 公式和 Gauss 公式,并会利用 它们计算积分。 第五章 无穷级数 12.1 常数项级数的概念和性质 12.2 常数项级数的审敛法 12.3 幂级数 12.4 函数展开成幂级数 12.5 傅里叶级数* 知识点: 1. 理解数项级数收敛、发散及收敛级数和的 概念,掌握级数的基本性质及收敛的必要条 件。 2. 掌握几何级数、p-级数和级数收敛与发散 的条件。 3. 掌握正项级数收敛性的比较判别法,比值 判别法和根值判别法。 4. 了解任意项数的绝对收敛与条件收敛的概 念及关系,掌握交错级数的 Leibniz 判别法。 5. 了解函数项级数的收敛域及和函数的概 念。 6. 掌握幂级数的收敛半径,收敛区间的求 法。 7. 了解幂级数的连续性、逐项微分和逐项积 分等性质,并能利用这些性质求一些幂级数 的和函数与某些数项级数的和。 8. 了解 Taylor 级数与余项公式,掌握基本初 级函数的 Taylor 展开。 自学内容:常数项级数的概念,级数的性 质;幂级数的应用(求数项级数的和、近 似计算、欧拉公式);傅立叶级数; 课堂作业: 教材思考题、习题 课外作业: 同步辅导书、习题
9.了解傅里叶级数。 五、建议学时分配表 学时分配 序号 课程内容 对应教学目标 讲授 实验 习题课 小计 1空间解析几何 16 16 目标1 2多元函数微分法及其应用 18 18 目标1 3 3重积分 14 2 16 目标2、目标3 4 4曲线积分与曲面积分 14 2 16 目标2、目标3 目标2、目标 5无穷级数 12 2 14 3、目标4 合计 82 6 88 六、教学方法(本课程的主要教学方法) 本课程主要采用课堂教学法通过讲解和学生堂下练习相结合的方式推进教学,具体内容包括: 1,课堂教学中注重讲练结合,课堂教学中的师生的交流方式多样化,采用启发式教学,培 养学生独立思考、分析问题和解决问题的能力。 2.充分利用现代化教学手段,让多媒体教学与传统板书相结合,提高课堂教学信息量,利 用网络资源丰富教学手段。 3.课堂练习及课后作业处理方式多样化,注重利用教学信息回馈带来的正效应丰富课堂教 学内涵。 七、课程考核内容及方式 (考核方式、重点考核内容、各部分成绩占比、预期目标等) 1考核方式考试 2.考核形式包括平时考核、中期考核、期末考核等综合评定 3成绩评定采用百分制制,按以下3项考核指标进行实验成绩综合评定,其构成比例如下: (1)平时考核成绩:占课程总成绩的30%(其中考勤占10%,作业占10%,课堂表现占 10%); (2)期中考核成绩:占课程总成绩的10%; (3)期末考核成绩:占课程总成绩的60%: 13
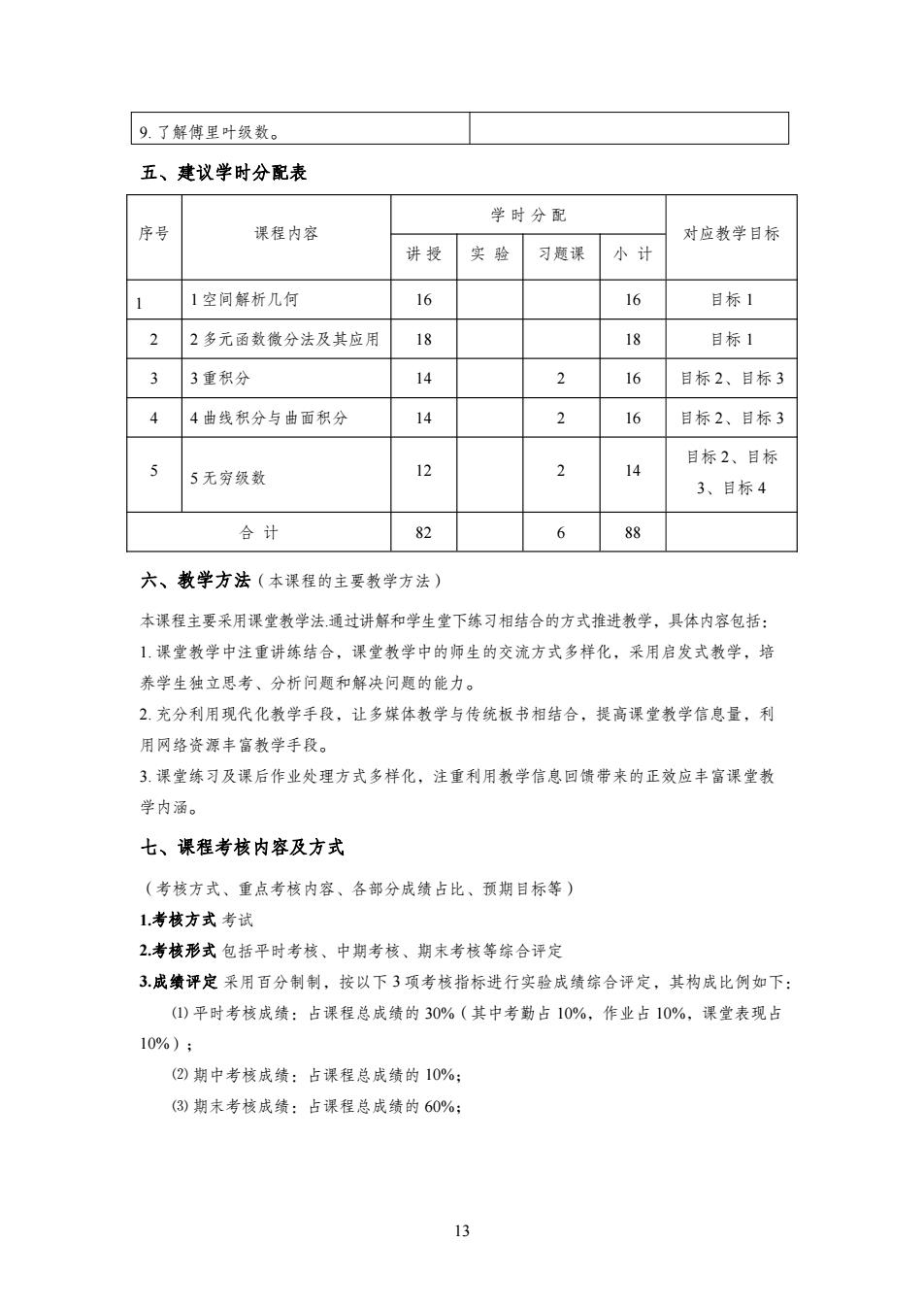
13 9. 了解傅里叶级数。 五、建议学时分配表 序号 课程内容 学 时 分 配 对应教学目标 讲 授 实 验 习题课 小 计 1 1 空间解析几何 16 16 目标 1 2 2 多元函数微分法及其应用 18 18 目标 1 3 3 重积分 14 2 16 目标 2、目标 3 4 4 曲线积分与曲面积分 14 2 16 目标 2、目标 3 5 5 无穷级数 12 2 14 目标 2、目标 3、目标 4 合 计 82 6 88 六、教学方法(本课程的主要教学方法) 本课程主要采用课堂教学法.通过讲解和学生堂下练习相结合的方式推进教学,具体内容包括: 1. 课堂教学中注重讲练结合,课堂教学中的师生的交流方式多样化,采用启发式教学,培 养学生独立思考、分析问题和解决问题的能力。 2. 充分利用现代化教学手段,让多媒体教学与传统板书相结合,提高课堂教学信息量,利 用网络资源丰富教学手段。 3. 课堂练习及课后作业处理方式多样化,注重利用教学信息回馈带来的正效应丰富课堂教 学内涵。 七、课程考核内容及方式 (考核方式、重点考核内容、各部分成绩占比、预期目标等) 1.考核方式 考试 2.考核形式 包括平时考核、中期考核、期末考核等综合评定 3.成绩评定 采用百分制制,按以下 3 项考核指标进行实验成绩综合评定,其构成比例如下: ⑴ 平时考核成绩:占课程总成绩的 30%(其中考勤占 10%,作业占 10%,课堂表现占 10%); ⑵ 期中考核成绩:占课程总成绩的 10%; ⑶ 期末考核成绩:占课程总成绩的 60%;