
第11卷第6期 智能系统学报 Vol.11 No.6 2016年12月 CAAI Transactions on Intelligent Systems Dec.2016 D0I:10.11992/is.201611017 网络出版地址:http://www.cnki.net/kcms/detail,/23.1538.TP.20170111.1705.026.html 基于相关性的小波熵心电信号去噪算法 王晓燕,鲁华祥12,金敏,龚国良',毛文宇1,陈刚 (1.中国科学院半导体研究所,北京100083;2.中国科学院脑科学与智能技术卓越创新中心,上海200031) 摘要:针对心电信号的基线漂移、工频噪声、肌电噪声,本文提出了基于相关性的小波嫡去噪算法。算法首先根据 基线漂移的低频特性,确定小波分解的层数,置零近似系数,去除基线漂移:再对相邻尺度的高频小波系数进行相关 处理,依据小波嫡自适应地计算全局阈值去除工频和肌电噪声:最后将置零的近似系数和阈值处理后的小波系数重 构得到有效信号。该算法能够在一次小波分解、重构的过程中,同时滤除心电信号中的3种主要噪声。对MTBH 数据库数据和模拟数据的仿真实验结果也表明该算法的去噪效果显著优于其他算法。 关键词:心电信号:去噪:相关性:小波嫡:自适应 中图分类号:TP391文献标志码:A文章编号:1673-4785(2016)06-0827-08 中文引用格式:王晓燕,鲁华祥,金敏,等.基于相关性的小波熵心电信号去噪算法[J].智能系统学报,2016,11(6):827-834. 英文引用格式:WANG Xiaoyan,LU Huaxiang,JIN Min,etal.Wavelet entropy denoising algorithm of electrocardiogram signals based on correlation[J].CAAI Transactions on Intelligent Systems,2016,11(6):827-834. Wavelet entropy denoising algorithm of electrocardiogram signals based on correlation WANG Xiaoyan',LU Huaxiang'2,JIN Min',GONG Guoliang',MAO Wenyu',CHEN Gang' (1.Institute of Semiconductors,Chinese Academy of Sciences,Beijing 100083,China;2.Center for Excellence in Brain Science and Intelligence Technology,Chinese Academy of Sciences,Shanghai 200031,China) Abstract:In view of the baseline drift,power line interference and muscle noise of electrocardiogram (ECG)sig- nals,the wavelet entropy denoising algorithm of ECG signals based on correlation was proposed.First,ECG signals were decomposed using wavelets to determine the number of scale of wavelet decomposition,and the lowest approxi- mation coefficients were each set to zero,so as to remove the baseline drift.Then,the high-frequency wavelet coef- ficient of adjacent scales was processed by adaptively calculating the global threshold with the correlation coeffi- cients between the adjacent scales,to remove the power line interference and the muscle noise.Last,the denoising signals were reconstructed using zero approximation coefficients and processed wavelet coefficients.Using this meth- od,three kinds of noise were removed in one process of wavelet decomposition and reconstruction.Experiments u- sing the MIT-BIH database and simulative data prove that the algorithm is much better than others in ECG denoising with low complexity. Keywords:electrocardiogram signals;denoising;correlation;wavelet entropy:adaptively 心电信号是心脏电活动在体表的综合表现,心应用十分广泛。然而心电信号在测量时不可避免地 电信号诊断因可靠、简便、对患者无创等优点,临床存在一些强干扰和噪声,如基线漂移、工频噪声、肌 电噪声和环境噪声等)。如何有效排除各种噪声, 收稿日期:2016-11-15. 基金项目:中国科学院战略性先导专项(d山02080002):青年自然科学准确提取出有用的心电信号波形,是临床心脏病智 基金项目(61401423);中国科学院国防实验室基金项目能诊断的重要基础。 (CXJ-16S076). 通信作者:鲁华祥.E-mail:luhr@semi.ac.cm 心电信号的频率在0.05~100Hz之间,其中
第 11 卷第 6 期 智 能 系 统 学 报 Vol.11 №.6 2016 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2016 DOI:10.11992 / tis.201611017 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20170111.1705.026.html 基于相关性的小波熵心电信号去噪算法 王晓燕1 ,鲁华祥1,2 ,金敏1 ,龚国良1 ,毛文宇1 ,陈刚1 (1. 中国科学院 半导体研究所,北京 100083; 2. 中国科学院 脑科学与智能技术卓越创新中心,上海 200031) 摘 要:针对心电信号的基线漂移、工频噪声、肌电噪声,本文提出了基于相关性的小波熵去噪算法。 算法首先根据 基线漂移的低频特性,确定小波分解的层数,置零近似系数,去除基线漂移;再对相邻尺度的高频小波系数进行相关 处理,依据小波熵自适应地计算全局阈值去除工频和肌电噪声;最后将置零的近似系数和阈值处理后的小波系数重 构得到有效信号。 该算法能够在一次小波分解、重构的过程中,同时滤除心电信号中的 3 种主要噪声。 对 MIT⁃BIH 数据库数据和模拟数据的仿真实验结果也表明该算法的去噪效果显著优于其他算法。 关键词:心电信号;去噪;相关性;小波熵;自适应 中图分类号: TP391 文献标志码:A 文章编号:1673-4785(2016)06-0827-08 中文引用格式:王晓燕,鲁华祥,金敏,等. 基于相关性的小波熵心电信号去噪算法[J]. 智能系统学报, 2016, 11(6): 827-834. 英文引用格式:WANG Xiaoyan, LU Huaxiang, JIN Min, et al. Wavelet entropy denoising algorithm of electrocardiogram signals based on correlation[J]. CAAI Transactions on Intelligent Systems, 2016, 11(6): 827-834. Wavelet entropy denoising algorithm of electrocardiogram signals based on correlation WANG Xiaoyan 1 , LU Huaxiang 1,2 , JIN Min 1 , GONG Guoliang 1 , MAO Wenyu 1 , CHEN Gang 1 (1. Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China; 2. Center for Excellence in Brain Science and Intelligence Technology, Chinese Academy of Sciences, Shanghai 200031, China) Abstract: In view of the baseline drift, power line interference and muscle noise of electrocardiogram (ECG) sig⁃ nals, the wavelet entropy denoising algorithm of ECG signals based on correlation was proposed. First, ECG signals were decomposed using wavelets to determine the number of scale of wavelet decomposition, and the lowest approxi⁃ mation coefficients were each set to zero, so as to remove the baseline drift. Then, the high⁃frequency wavelet coef⁃ ficient of adjacent scales was processed by adaptively calculating the global threshold with the correlation coeffi⁃ cients between the adjacent scales, to remove the power line interference and the muscle noise. Last, the denoising signals were reconstructed using zero approximation coefficients and processed wavelet coefficients. Using this meth⁃ od, three kinds of noise were removed in one process of wavelet decomposition and reconstruction. Experiments u⁃ sing the MIT⁃BIH database and simulative data prove that the algorithm is much better than others in ECG denoising with low complexity. Keywords: electrocardiogram signals; denoising; correlation; wavelet entropy; adaptively 收稿日期:2016-11-15. 基金项目:中国科学院战略性先导专项( xdb02080002);青年自然科学 基金项目( 61401423); 中国科学院国防实验室基金项目 (CXJJ⁃16S076). 通信作者:鲁华祥. E⁃mail: luhx@ semi.ac.cn. 心电信号是心脏电活动在体表的综合表现,心 电信号诊断因可靠、简便、对患者无创等优点,临床 应用十分广泛。 然而心电信号在测量时不可避免地 存在一些强干扰和噪声,如基线漂移、工频噪声、肌 电噪声和环境噪声等[1] 。 如何有效排除各种噪声, 准确提取出有用的心电信号波形,是临床心脏病智 能诊断的重要基础。 心电信号的频率在 0. 05 ~ 100 Hz 之间,其中

.828 智能系统学报 第11卷 90%的能量集中在0.25~35Hz之间。而心电信号 式中:s(t)为原始信号;j为分解层数;H、G为小波 噪声主要有50Hz/60Hz及其谐波组成的工频千 分解滤波器系数:A,为信号在层的近似部分(即低 扰、5~2kHz的肌电千扰以及频率小于0.5Hz的基 频部分)的近似系数;W,为信号s(t)在第j层的细 线漂移等)。目前常用的方法主要有形态学滤波 节系数(即高频部分)的小波系数。 法[)、EMD分解法[、基于小波理论的小波阈值 小波去噪的根本任务是在小波域将信号的小波 法s-刀、小波嫡阈值去噪法[劉以及相关方法的结 变换与噪声的小波变换有效地分离。由于有效信号 合【9-0]等。形态学滤波法处理基线漂移效果完美, 分解后的小波系数绝对值比较大,而噪声信号的能 但处理高频噪声会产生阶段误差。基于EMD分解 量相对分散,表现为小波分解后的小波系数绝对值 法能够对信号自适应地从高频到低频分解为固有模 较小,因此可以通过阈值处理方法进行去噪。当小 态函数,根据噪声一般分布的频段,直接舍弃某些高 波变换系数小于阈值时,认为主要由噪声引起,予以 频分量和低频分量,在去掉噪声的同时也会去掉一 舍弃:当小波系数大于阈值时,认为主要由信号引 部分原始信号。小波变换是一种信号的时间-频率 起,予以保留:然后用新的近似系数和小波系数进行 分析方法,具有多分辨率的特征,去除心电噪声效果 重构得到去噪后的信号。 显著。小波阈值去噪法在计算噪声方差时,通常将 信号与噪声的分离关键在于阈值的选择,Dono- 最高一层高频小波系数看作噪声,求取其作为噪声 ho提出的阈值计算公式如式(3)所示: 方差,具有一定误差。文献[8]中的基于小波嫡的 去噪法,对高频小波系数进行处理,高频噪声去除效 thr=o√2log(N) (3) 果良好,但忽略了低频近似系数的影响,基线漂移去 式中:c=median(|W.tl)/0.6745,W.k为尺度上点 除效果不理想。 的小波系数。通常直接对最高一层高频小波系数取 针对以上问题,本文提出一种基于相关性的小 中值作为噪声方差,认为这一层高频小波系数都是 波嫡心电信号去噪方法。首先对信号进行小波分 由噪声引起的,而忽略了高频小波系数中除了噪声 解,对基线漂移,通过置零近似系数去除;对肌电噪 以外仍可能含有的有效信号。如何选取阈值是关 声和工频噪声,需要在高频小波系数中对信号和噪 键,因此本文提出了一种基于小波嫡和相关性的阈 声进行区分,利用各尺度间有效信号和噪声相关性 值选取方法。 不同的特性,对高频小波系数进行相关性处理,将有 效信号和噪声分离,从而利用噪声计算小波熵阈值。 2 基于相关性的小波熵阈值去噪算法 最后将置零的近似系数和各尺度阈值处理后的高频 2.1算法的基本思想 系数进行重构,得到去噪信号。算法充分利用不同 对含噪信号进行小波分解后得到低频近似系数 类型的噪声特性,能够在一次小波分解、重构的过程 中同时滤除心电信号的3种主要噪声,且根据信号 和高频小波系数。一般将低于0.5Hz的低频分量看 能量自适应地选取阈值的方式,能够在提高信噪比 作基线漂移,为去除基线漂移,算法根据基线漂移的 的同时更好地保护有效信号。本文最后利用MT- 低频特性来确定小波分解的层数,使分解得到的最低 BH标准心电数据库等检验了所提算法,仿真实验 频的近似系数的频率范围接近基线漂移的频率范围, 结果表明,算法复杂度低,且去噪效果显著优于目前 再将最低频的近似系数置零即去掉基线漂移。 典型的心电去噪算法。 工频和肌电噪声和心电信号频谱有重叠,需要 1 小波阈值去噪算法 在高频小波系数中进行处理。根据有效信号的小波 系数在各尺度间具有较强的相关性,而噪声的小波 假设含噪信号由式(1)表示: 系数在各尺度间无明显的相关性,可以区分有效信 s(t)=f(t)+e(t) (1) 号和噪声。对高频小波系数进行相关性分析,确定 式中:t为时间序列,t=1,2,…,N,s(t)为含噪信 噪声夹杂的有效信号的位置,并将这些有效信号置 号;f(t)为原始信号,e(t)为噪声。 零:设置噪声能量阈值,循环多次剔除有效信号从而 小波变换是一种信号的多尺度分析方法,离散 小波分解通过Mallet算法[门实现,如式(2)。 得到各尺度新的高频小波系数。如果忽略对高频小 [A[s(t)]=s(t) 波系数的相关性处理工作,在去噪过程中会因为未 有效区分噪声,导致有效信号损失。小波嫡作为小 A,[s()]=∑H(21-k)A-[s()] 2) 波变换与信息嫡的结合,可以在时频域上对信息的 Ws(t)]=∑G(2-k)W-[s()] 能量做出度量[)。将经过相关性分析的高频小波 系数等分为若干区间,计算各区间的小波嫡值,选取
90%的能量集中在 0.25 ~ 35 Hz 之间。 而心电信号 噪声主要有 50 Hz/ 60 Hz 及其谐波组成的工频干 扰、5~2k Hz 的肌电干扰以及频率小于 0.5 Hz 的基 线漂移等[2] 。 目前常用的方法主要有形态学滤波 法[3] 、EMD 分解法[4] 、基于小波理论的小波阈值 法[5-7] 、小波熵阈值去噪法[8] 以及相关方法的结 合[9-10]等。 形态学滤波法处理基线漂移效果完美, 但处理高频噪声会产生阶段误差。 基于 EMD 分解 法能够对信号自适应地从高频到低频分解为固有模 态函数,根据噪声一般分布的频段,直接舍弃某些高 频分量和低频分量,在去掉噪声的同时也会去掉一 部分原始信号。 小波变换是一种信号的时间-频率 分析方法,具有多分辨率的特征,去除心电噪声效果 显著。 小波阈值去噪法在计算噪声方差时,通常将 最高一层高频小波系数看作噪声,求取其作为噪声 方差,具有一定误差。 文献[8] 中的基于小波熵的 去噪法,对高频小波系数进行处理,高频噪声去除效 果良好,但忽略了低频近似系数的影响,基线漂移去 除效果不理想。 针对以上问题,本文提出一种基于相关性的小 波熵心电信号去噪方法。 首先对信号进行小波分 解,对基线漂移,通过置零近似系数去除;对肌电噪 声和工频噪声,需要在高频小波系数中对信号和噪 声进行区分,利用各尺度间有效信号和噪声相关性 不同的特性,对高频小波系数进行相关性处理,将有 效信号和噪声分离,从而利用噪声计算小波熵阈值。 最后将置零的近似系数和各尺度阈值处理后的高频 系数进行重构,得到去噪信号。 算法充分利用不同 类型的噪声特性,能够在一次小波分解、重构的过程 中同时滤除心电信号的 3 种主要噪声,且根据信号 能量自适应地选取阈值的方式,能够在提高信噪比 的同时更好地保护有效信号。 本文最后利用 MIT⁃ BIH 标准心电数据库等检验了所提算法,仿真实验 结果表明,算法复杂度低,且去噪效果显著优于目前 典型的心电去噪算法。 1 小波阈值去噪算法 假设含噪信号由式(1)表示: s(t) = f(t) + e(t) (1) 式中: t 为时间序列, t = 1,2,…,N , s(t) 为含噪信 号; f(t) 为原始信号, e(t) 为噪声。 小波变换是一种信号的多尺度分析方法,离散 小波分解通过 Mallet 算法[11]实现,如式(2)。 A0 [s(t)] = s(t) Aj[s(t)] = ∑k H(2t - k)Aj-1 [s(t)] Wj[s(t)] = ∑k G(2t - k)Wj-1 [s(t)] ì î í ï ï ï ï ïï (2) 式中: s(t) 为原始信号; j 为分解层数; H、G 为小波 分解滤波器系数; Aj 为信号在层的近似部分(即低 频部分)的近似系数; Wj 为信号 s(t) 在第 j 层的细 节系数(即高频部分)的小波系数。 小波去噪的根本任务是在小波域将信号的小波 变换与噪声的小波变换有效地分离。 由于有效信号 分解后的小波系数绝对值比较大,而噪声信号的能 量相对分散,表现为小波分解后的小波系数绝对值 较小,因此可以通过阈值处理方法进行去噪。 当小 波变换系数小于阈值时,认为主要由噪声引起,予以 舍弃;当小波系数大于阈值时,认为主要由信号引 起,予以保留;然后用新的近似系数和小波系数进行 重构得到去噪后的信号。 信号与噪声的分离关键在于阈值的选择,Dono⁃ ho 提出的阈值计算公式如式(3)所示: thr = σ 2log(N) (3) 式中: σ = median( Wj,k ) / 0.674 5, Wj,k 为尺度上点 的小波系数。 通常直接对最高一层高频小波系数取 中值作为噪声方差,认为这一层高频小波系数都是 由噪声引起的,而忽略了高频小波系数中除了噪声 以外仍可能含有的有效信号。 如何选取阈值是关 键,因此本文提出了一种基于小波熵和相关性的阈 值选取方法。 2 基于相关性的小波熵阈值去噪算法 2.1 算法的基本思想 对含噪信号进行小波分解后得到低频近似系数 和高频小波系数。 一般将低于 0.5 Hz 的低频分量看 作基线漂移,为去除基线漂移,算法根据基线漂移的 低频特性来确定小波分解的层数,使分解得到的最低 频的近似系数的频率范围接近基线漂移的频率范围, 再将最低频的近似系数置零即去掉基线漂移。 工频和肌电噪声和心电信号频谱有重叠,需要 在高频小波系数中进行处理。 根据有效信号的小波 系数在各尺度间具有较强的相关性,而噪声的小波 系数在各尺度间无明显的相关性,可以区分有效信 号和噪声。 对高频小波系数进行相关性分析,确定 噪声夹杂的有效信号的位置,并将这些有效信号置 零;设置噪声能量阈值,循环多次剔除有效信号从而 得到各尺度新的高频小波系数。 如果忽略对高频小 波系数的相关性处理工作,在去噪过程中会因为未 有效区分噪声,导致有效信号损失。 小波熵作为小 波变换与信息熵的结合,可以在时频域上对信息的 能量做出度量[12] 。 将经过相关性分析的高频小波 系数等分为若干区间,计算各区间的小波熵值,选取 ·828· 智 能 系 统 学 报 第 11 卷

第6期 王晓燕,等:基于相关性的小波嫡心电信号去噪算法 .829. 最大小波嫡值子区间的高频小波系数平均值的绝对 2 值作为噪声方差。这种方法在一定程度上减少了阈 sgn(W)W.iathr),W thr 1+e N 值选取的盲目性。 0 Wil<thr 2.2相关性计算 相关系数计算公式如式(4)所示: (11) C.k=W.k·W+1.k (4) 式中:W体为小波系数;W,:为阈值处理后的小波系 式中:C.为分解尺度j上k点的相关系数,W法和 数:hr为全局阈值。阈值计算函数如式(3)。该阈 W+1分别为尺度j和尺度j+1上k点的小波系数。 值函数结合了软硬阈值的优点,具有连续性强的特 为使相关系数与小波系数具有可比性,需要定 点,避免信号降噪后的震荡现象,同时高阶可导。 义规范化相关系数),定义(5)为C的规范化相 2.5算法流程 关系数: 1)根据基线漂移的低频特性设置小波分解层 数,对含噪信号进行多尺度分解,得到最低频的近似 N.(j,k)=Cj/P.(j)/P.(j) (5) 系数和各尺度高频小波系数。 式中:N(,k)为尺度j上k点的规范化系数,并且 2)将低频近似系数置零,去除基线漂移。 P.G)=∑W2,P.G)=∑Ct2。 3)选取有限个样本的方差作为初始噪声的方 显然,在尺度j下,小波系数W与规范化相关 差14],这里采用最高频小波系数的前80个点估计 系数具有相同的能量,这为它们之间提供了可比性。 初始噪声,计算方差sigma1,设置阈值k。 记录各尺度规范化相关系数大于高频小波系数的位 4)将相邻尺度的高频小波系数进行相关性计 置,该位置即为各尺度高频小波系数中有效信号的 算,将系数大于规范化系数的位置上的小波系数置 位置,并将该位置的高频小波系数置零,得到新的高 零,剩下的为噪声产生的系数,从而估计噪声方差 频小波系数,认为其全部是由噪声引起的,由这些系 sigma2o 数计算噪声方差。 5)若sigma.2>k·sigma1,返回4),否则,利用 2.3小波熵 sigma,和小波嫡计算全局阈值。 6)对每一层的高频小波系数利用全局阈值进 对信号进行1尺度分解,设尺度上的小波系数 行处理。并将新低频近似系数和新高频小波系数进 为W,=(W.1,W.2,…,W.N)。若小波基函数为正交 基,尺度j的小波变换满足能量守恒原则。因此,尺 行重构,得到去噪后的信号。 度j的小波能量E,等于该尺度小波系数的平方和, 3数据仿真与实验结果 如式(6)所示: 本文在intel Core i5-3470CPU+4G内存的计算 2 (6) 机平台上,使MATLAB软件编程实现对信号的仿真 实验,选取的小波函数为bior3.7小波。 式中N为采样点数。信号的总能量计算公式如式 3.1数据来源和评价标准 (7)所示: 实验针对心电信号进行定性和定量仿真实验。 E= (7) 定性实验数据采用来自MT-BIH6]心律失常数据 k=1 由式(6)和式(7)可以确定第j层小波系数的信 库(Arrhythmia Database)和MT-BIH噪声数据库 号能量在总能量中存在的概率为 (即Nstdb Database)中真实的心电数据。定量实验 为方便计算,利用MATLAB模拟干净的心电信号。 P;=E/E (8) 本文的方法是在分析小波系数相邻尺度相关性 已知概率,可以确定信号小波熵S1)为 和小波嫡的基础上提出来的,为了验证所提算法的 S=- ∑pnp (9) 优越性,使用信噪比(SNR)、均方根误差(MSE)和 运行时间T3个指标来进行衡量和比较。信噪比和 2.4 阈值处理 本文提出的噪声方差计算公式如式(10): 均方根误差公式如式(12)、(13): o=abs(mean(W.t)) (10) =1 采用的阈值处理函数如式(11): SNR=10·log (12) Wk三 [s(t)-s(t)]2
最大小波熵值子区间的高频小波系数平均值的绝对 值作为噪声方差。 这种方法在一定程度上减少了阈 值选取的盲目性。 2.2 相关性计算 相关系数计算公式如式(4)所示: Cj,k = Wj,k·Wj+1,k (4) 式中: Cj,k 为分解尺度 j 上 k 点的相关系数, Wj,k 和 Wj+1,k 分别为尺度 j 和尺度 j + 1 上 k 点的小波系数。 为使相关系数与小波系数具有可比性,需要定 义规范化相关系数[13] ,定义(5)为 Cj,k 的规范化相 关系数: Nc(j,k) = Cj,k Pw(j) / Pc(j) (5) 式中: Nc (j,k) 为尺度 j 上 k 点的规范化系数,并且 Pw(j) = ∑k Wj,k 2 , Pc(j) = ∑k Cj,k 2 。 显然,在尺度 j 下,小波系数 Wj,k 与规范化相关 系数具有相同的能量,这为它们之间提供了可比性。 记录各尺度规范化相关系数大于高频小波系数的位 置,该位置即为各尺度高频小波系数中有效信号的 位置,并将该位置的高频小波系数置零,得到新的高 频小波系数,认为其全部是由噪声引起的,由这些系 数计算噪声方差。 2.3 小波熵 对信号进行 l 尺度分解,设尺度 j 上的小波系数 为 Wj = (Wj,1 ,Wj,2 ,…,Wj,N) 。 若小波基函数为正交 基,尺度 j 的小波变换满足能量守恒原则。 因此,尺 度 j 的小波能量 Ej 等于该尺度小波系数的平方和, 如式(6)所示 : Ej = ∑ N k = 1 Wj,k 2 (6) 式中 N 为采样点数。 信号的总能量计算公式如式 (7)所示: E = ∑ N k = 1 Ej (7) 由式(6)和式(7)可以确定第 j 层小波系数的信 号能量在总能量中存在的概率为 pj = Ej / E (8) 已知概率,可以确定信号小波熵 S [15]为 S = - ∑ l j = 1 pj ln pj (9) 2.4 阈值处理 本文提出的噪声方差计算公式如式(10): σ = abs(mean(Wj,k)) (10) 采用的阈值处理函数如式(11): Wj,k = sgn(Wj,k)( Wj,k - 2 1 + e Wj,k -thr N thr), Wj,k ≥ thr 0, Wj,k < thr ì î í ï ï ï ï (11) 式中: Wj,k 为小波系数; Wj,k 为阈值处理后的小波系 数;thr 为全局阈值。 阈值计算函数如式(3)。 该阈 值函数结合了软硬阈值的优点,具有连续性强的特 点,避免信号降噪后的震荡现象,同时高阶可导。 2.5 算法流程 1)根据基线漂移的低频特性设置小波分解层 数,对含噪信号进行多尺度分解,得到最低频的近似 系数和各尺度高频小波系数。 2)将低频近似系数置零,去除基线漂移。 3)选取有限个样本的方差作为初始噪声的方 差[14] ,这里采用最高频小波系数的前 80 个点估计 初始噪声,计算方差 sigma1 ,设置阈值 k 。 4)将相邻尺度的高频小波系数进行相关性计 算,将系数大于规范化系数的位置上的小波系数置 零,剩下的为噪声产生的系数,从而估计噪声方差 sigma2 。 5)若 sigma2 > k ·sigma1 ,返回 4),否则,利用 sigma2 和小波熵计算全局阈值。 6)对每一层的高频小波系数利用全局阈值进 行处理。 并将新低频近似系数和新高频小波系数进 行重构,得到去噪后的信号。 3 数据仿真与实验结果 本文在 Intel Core i5⁃3470 CPU+4G 内存的计算 机平台上,使 MATLAB 软件编程实现对信号的仿真 实验,选取的小波函数为 bior3.7 小波。 3.1 数据来源和评价标准 实验针对心电信号进行定性和定量仿真实验。 定性实验数据采用来自 MIT⁃BIH [16] 心律失常数据 库( Arrhythmia Database) 和 MIT⁃BIH 噪声数据库 (即 Nstdb Database)中真实的心电数据。 定量实验 为方便计算,利用 MATLAB 模拟干净的心电信号。 本文的方法是在分析小波系数相邻尺度相关性 和小波熵的基础上提出来的,为了验证所提算法的 优越性,使用信噪比( SNR)、均方根误差(MSE) 和 运行时间 T 3 个指标来进行衡量和比较。 信噪比和 均方根误差公式如式(12)、(13): SNR = 10·log ∑ N t = 1 s 2 (t) ∑ N t = 1 s ^ [ (t) - s(t) ] 2 é ë ê ê ê ê ù û ú ú ú ú (12) 第 6 期 王晓燕,等:基于相关性的小波熵心电信号去噪算法 ·829·
830 智能系统学报 第11卷 RMSE= 0.08 N ,[s(t)-s(t)]2 (13) 式中:s(t)表示去噪后的信号;s(t)是去噪前的信 0.06 号;N为采样长度。 3.2对心律失常数据库信号去噪 0.04 MT-BIH心律失常数据库(Arrhythmia Data- base)中的心电数据含噪声较少,选取其100号数据 0.02 的前2048个数据作为本次研究的信号,人为加入 工频干扰、基线漂移和高频噪声(包括肌电干扰)3 50 100 种噪声。基线漂移、工频干扰和高频噪声分别来自 fHz MT-BIH噪声数据库(Nstdb Database)中的bw、em (b)加噪信号频谱图 和ma数据。本文算法与改进的小波阈值算法[)和 图2加噪信号波形及频谱图 小波嫡去噪算法[8劉对比,以输入信噪比为-2.6dB、 Fig.2 The waveform and spectrum of noisy signals 均方误差为0.2539为例,去噪效果如图1~5所示, 为方便观察基线漂移,显示前6个周期。 103 0 0.5 1.0 1.5 2.0 采样点 105 0.5 1.0 1.5 2.0 (a)改进的小波阈值算法去噪波形图 采样点 0.08 (a)原始信号波形图 0.06 0.08 。0.04 0.06 0.02 0.04 0.02 50 100 fHz (b)改进的小波阈值算法去噪频谱图 50 100 图3改进的小波阈值算法去噪波形及频谱图 fz Fig.3 The waveform and spectrum of de-nosing signals (b)原始信号频谱图 of improved wavelet threshold algorithm 图1原始信号波形及频谱图 Fig.1 The waveform and spectrum of original signals 2 .0 0.5 1.0 1.5 0.5 采样点 1.5 2.0*10 采样点 (a)小波嫡算法去噪波形图 (a)加噪信号波形图
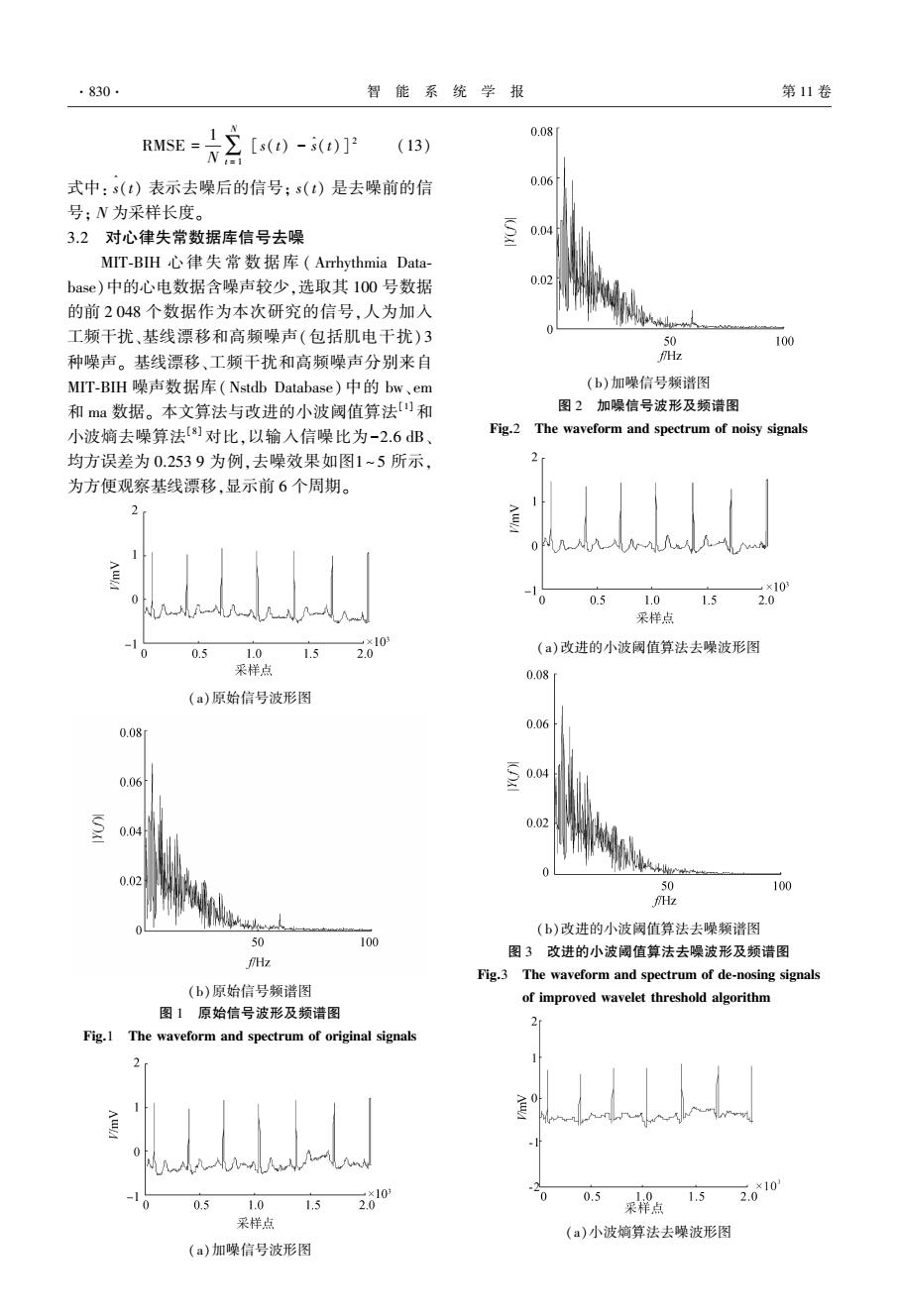
RMSE = 1 N∑ N t = 1 [s(t) - s ^ (t)] 2 (13) 式中: s ^ (t) 表示去噪后的信号; s(t) 是去噪前的信 号; N 为采样长度。 3.2 对心律失常数据库信号去噪 MIT⁃BIH 心 律 失 常 数 据 库 ( Arrhythmia Data⁃ base)中的心电数据含噪声较少,选取其 100 号数据 的前 2 048 个数据作为本次研究的信号,人为加入 工频干扰、基线漂移和高频噪声(包括肌电干扰) 3 种噪声。 基线漂移、工频干扰和高频噪声分别来自 MIT⁃BIH 噪声数据库(Nstdb Database) 中的 bw、em 和 ma 数据。 本文算法与改进的小波阈值算法[1] 和 小波熵去噪算法[8] 对比,以输入信噪比为-2.6 dB、 均方误差为 0.253 9 为例,去噪效果如图1~ 5 所示, 为方便观察基线漂移,显示前 6 个周期。 (a)原始信号波形图 (b)原始信号频谱图 图 1 原始信号波形及频谱图 Fig.1 The waveform and spectrum of original signals (a)加噪信号波形图 (b)加噪信号频谱图 图 2 加噪信号波形及频谱图 Fig.2 The waveform and spectrum of noisy signals (a)改进的小波阈值算法去噪波形图 (b)改进的小波阈值算法去噪频谱图 图 3 改进的小波阈值算法去噪波形及频谱图 Fig.3 The waveform and spectrum of de⁃nosing signals of improved wavelet threshold algorithm (a)小波熵算法去噪波形图 ·830· 智 能 系 统 学 报 第 11 卷
第6期 王晓燕,等:基于相关性的小波嫡心电信号去噪算法 ·831. 0.06 048个数据分别用3种去噪算进行去噪,结果如图6 ~9所示,为方便观察波形,对比去噪效果,波形只 0.04 显示3个周期。 0.02 50 100 fHz (b)小波熵算法去噪频谱图 图4小波熵算法去噪波形及频谱图 0.5 0 采样点 Fig.4 The waveform and spectrum of de- nosing signals of wavelet entropy al- (a)含噪信号波形图 gorithm 0.20 2 0.15 0.10 0.05 0 0.5 采样 1.5 30*10 0.5 1.0 fHz (a)本文算法去噪波形图 (b)含噪信号频谱图 0.08 图6含噪信号波形及频谱图 Fig.6 The waveform and spectrum of noisy signals 0.06 0.04 0.02 0.5 1.0 采样点 50 100 fHz (a)改进的小波阈值算法去噪波形图 (b)本文算法去噪频谱图 0.20 图5本文算法去噪波形及频谱图 Fig.5 The waveform and spectrum of de-nosing signals 0.15 of proposed algorithm 该数据库中工频噪声主要集中在60Hz左 0.10 右。可以看出,本文提出的基于相关性的小波嫡去 0.05 噪算法与目前两种典型的心电信号去噪算法相比, 基线漂移、60Hz工频干扰被很好地去除:波形连续 0 性强,无震荡现象,波形清晰完整,去除肌电噪声效 0.5 1.0 fHz 果显著。即可以在一次小波分解、重构的过程中同 时去除3种主要的心电信号噪声。 (b)改进的小波阈值算法去噪频谱图 3.3对噪声数据库信号去噪 图7改进的小波阈值算法去噪波形及频谱图 MIT-BIH噪声数据库(Nstd山Database)是真实 Fig.7 The waveform and spectrum of de-nosing signals of developed wavelet threshold algorithm 的带噪声的信号,对该数据库中11806信号的前2
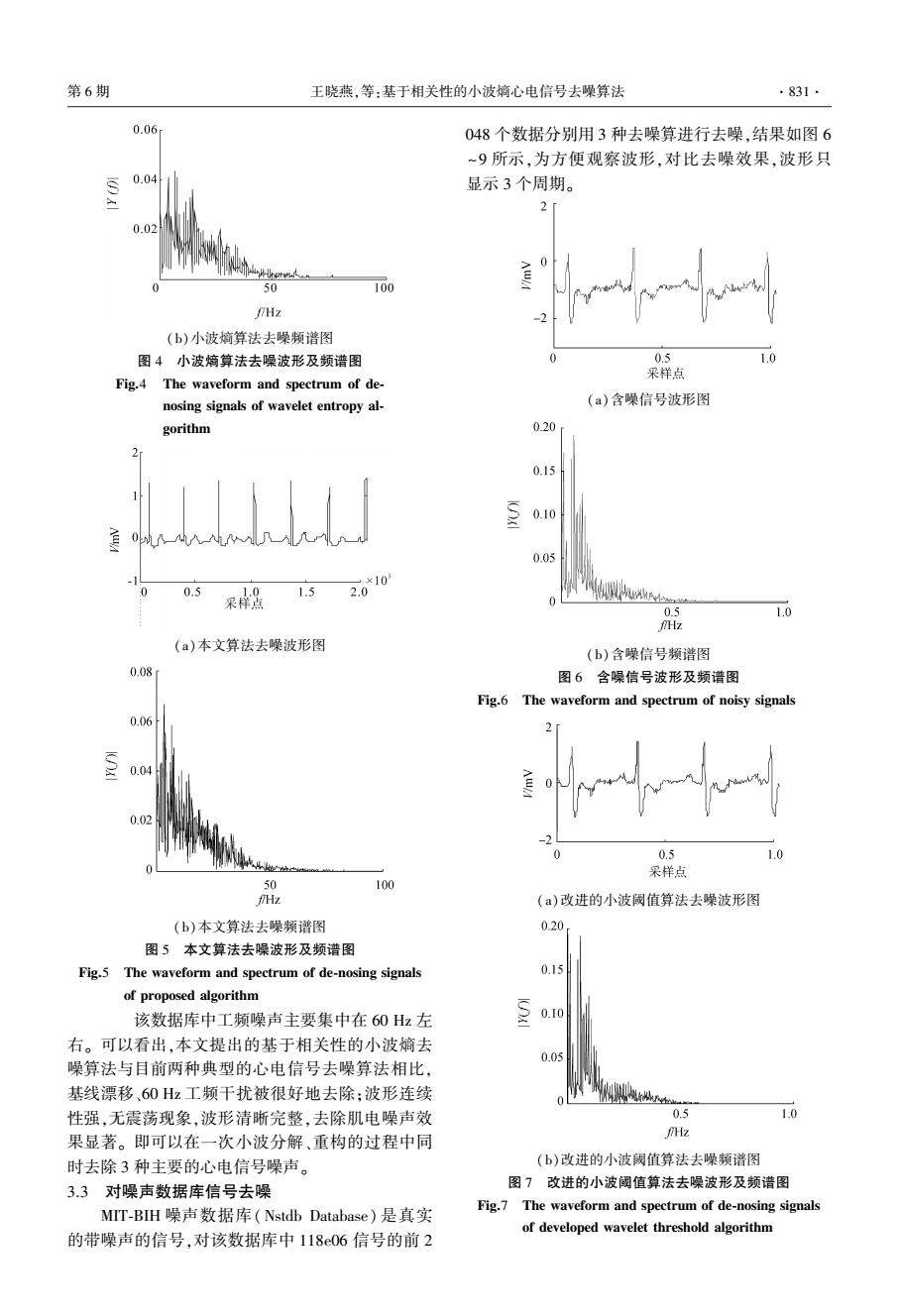
(b)小波熵算法去噪频谱图 图 4 小波熵算法去噪波形及频谱图 Fig.4 The waveform and spectrum of de⁃ nosing signals of wavelet entropy al⁃ gorithm (a)本文算法去噪波形图 (b)本文算法去噪频谱图 图 5 本文算法去噪波形及频谱图 Fig.5 The waveform and spectrum of de⁃nosing signals of proposed algorithm 该数据库中工频噪声主要集中在 60 Hz 左 右。 可以看出,本文提出的基于相关性的小波熵去 噪算法与目前两种典型的心电信号去噪算法相比, 基线漂移、60 Hz 工频干扰被很好地去除;波形连续 性强,无震荡现象,波形清晰完整,去除肌电噪声效 果显著。 即可以在一次小波分解、重构的过程中同 时去除 3 种主要的心电信号噪声。 3.3 对噪声数据库信号去噪 MIT⁃BIH 噪声数据库(Nstdb Database) 是真实 的带噪声的信号,对该数据库中 118e06 信号的前 2 048 个数据分别用 3 种去噪算进行去噪,结果如图 6 ~9 所示,为方便观察波形,对比去噪效果,波形只 显示 3 个周期。 (a)含噪信号波形图 (b)含噪信号频谱图 图 6 含噪信号波形及频谱图 Fig.6 The waveform and spectrum of noisy signals (a)改进的小波阈值算法去噪波形图 (b)改进的小波阈值算法去噪频谱图 图 7 改进的小波阈值算法去噪波形及频谱图 Fig.7 The waveform and spectrum of de⁃nosing signals of developed wavelet threshold algorithm 第 6 期 王晓燕,等:基于相关性的小波熵心电信号去噪算法 ·831·