
第12卷第4期 智能系统学报 Vol.12 No.4 2017年8月 CAAI Transactions on Intelligent Systems Aug.2017 D0I:10.11992/is.201605015 网络出版地址:http:/kns.cnki.net/kcms/detail/23.1538.tp.20170606.1114.006.html 差分进化算法综述 丁青锋,尹晓宇2 (1.华东交道大学电气与自动化工程学院,江西南昌330013:2.上海大学特种光纤与光接入重点实验室,上海200072) 摘要:差分进化算法由于算法结构简单易于执行,并且具有优化效率高、参数设置简单、鲁棒性好等优点,因此差 分进化算法吸引了越来越多研究者的关注。本文概述了差分进化算法的基本概念以及存在的问题,综述了差分进 化算法的控制参数、差分策略、种群结构以及与其他最优化算法混合等4个方面改进策略并讨论它们各自的优缺 点,为差分进化算法下一步的改进提出了参考方向。 关键词:差分进化:启发式并行搜索;差分策略;控制参数:种群结构;混合优化;收敛速度:优化效率 中图分类号:TP301文献标志码:A文章编号:1673-4785(2017)04-0431-12 中文引用格式:丁青锋,尹晓宇.差分进化算法综述[J].智能系统学报,2017,12(4):431-442. 英文引用格式:DING Qingfeng,YIN Xiaoyu..Research survey of differential evolution algorithms[J].CAAI transactions on intelligent systems,2017,12(4):431-442. Research survey of differential evolution algorithms DING Qingfeng',YIN Xiaoyu2 (1.School of Electrical and Automation Engineering,East China Jiaotong University,Nanchang 330013,China;2.Key Laboratory of Specialty Fiber Optics and Optical Access Networks,Shanghai University,Shanghai 200072,China) Abstract:Due to its simple algorithm structure,ease of performance,high optimization efficiency,simple parameter setting,and excellent robustness,the differential evolution (DE)algorithm has attracted increasing attention from researchers.In this paper,we outline the basic concepts of the DE algorithm as well as its limitations,and review four improvement strategies,including a control parameter,differential strategy,population structure,and mixing it with other optimization algorithms.We discuss the advantages and disadvantages of these strategies and suggest directions for future improvements to the DE algorithm. Keywords:differential evolution algorithm;heuristic parallel search;differential strategies;control parameter; population structure;mixed optimization;convergence rate;optimization efficiency 随着科技的进步和生产技术的发展,优化问题 数据”的涌现,现在的科学研究以及工程实践中优 几乎遍布科学研究及工程实践的各个领域,成为现 化问题通常具有规模大、复杂程度高以及包含大量 代科技不可或缺的理论基础和研究方法。而具有 局部最优解等特点,很多优化问题并没有明确的数 启发式和随机特性的进化算法,如遗传算法(genetic 学解析式,或者其本身就是非确定性多项式难题 algorithm,GA)[)、进化规划(evolution programming, (non-deterministic polynomial,NP),现有研究成果及 EP)[2)以及进化策略(evolution strategy,ES)l)具有 方法远远不能满足。 算法效率高、易操作以及简单通用等特点,也成为 差分进化算法(differential evolution,DE)作为 解决现实世界中优化问题的有效工具,取得了一些 一种新型、高效的启发式并行搜索技术,通过对现 有效的成果。但随着信息时代的快速发展以及“大 有优化方法进行大胆的扬弃,具有收敛快、控制参 数少且设置简单、优化结果稳健等优点[,对进化 收稿日期:2016-05-17.网络出版日期:2017-06-06 算法的理论和应用研究具有重要的学术意义。但 基金项目:国家自然科学基金项目(61501186):江西省普通本科高校中 青年教师发展计划访问学者专项资金项目:江西省自然科学 是,标准的DE算法也具有控制参数选择的压力大 基金项目(20171BAB202001):江西省教育厅科学基金项目 以及搜索能力与开发能力相矛盾的现象,往往容易 (GJ150491). 通信作者:丁青锋.E-mail:brandy724@sina.com
第 12 卷第 4 期 智 能 系 统 学 报 Vol.12 №.4 2017 年 8 月 CAAI Transactions on Intelligent Systems Aug. 2017 DOI:10.11992 / tis.201605015 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.tp.20170606.1114.006.html 差分进化算法综述 丁青锋1 ,尹晓宇2 (1.华东交通大学 电气与自动化工程学院,江西 南昌 330013; 2.上海大学 特种光纤与光接入重点实验室,上海 200072) 摘 要:差分进化算法由于算法结构简单易于执行,并且具有优化效率高、参数设置简单、鲁棒性好等优点,因此差 分进化算法吸引了越来越多研究者的关注。 本文概述了差分进化算法的基本概念以及存在的问题,综述了差分进 化算法的控制参数、差分策略、种群结构以及与其他最优化算法混合等 4 个方面改进策略并讨论它们各自的优缺 点,为差分进化算法下一步的改进提出了参考方向。 关键词:差分进化;启发式并行搜索;差分策略;控制参数;种群结构;混合优化;收敛速度;优化效率 中图分类号:TP301 文献标志码:A 文章编号:1673-4785(2017)04-0431-12 中文引用格式:丁青锋,尹晓宇.差分进化算法综述[J]. 智能系统学报, 2017, 12(4): 431-442. 英文引用格 式: DING Qingfeng, YIN Xiaoyu. Research survey of differential evolution algorithms [ J ]. CAAI transactions on intelligent systems, 2017, 12(4): 431-442. Research survey of differential evolution algorithms DING Qingfeng 1 , YIN Xiaoyu 2 (1. School of Electrical and Automation Engineering, East China Jiaotong University, Nanchang 330013, China; 2.Key Laboratory of Specialty Fiber Optics and Optical Access Networks, Shanghai University, Shanghai 200072, China) Abstract:Due to its simple algorithm structure, ease of performance, high optimization efficiency, simple parameter setting, and excellent robustness, the differential evolution ( DE) algorithm has attracted increasing attention from researchers. In this paper, we outline the basic concepts of the DE algorithm as well as its limitations, and review four improvement strategies, including a control parameter, differential strategy, population structure, and mixing it with other optimization algorithms. We discuss the advantages and disadvantages of these strategies and suggest directions for future improvements to the DE algorithm. Keywords: differential evolution algorithm; heuristic parallel search; differential strategies; control parameter; population structure; mixed optimization; convergence rate; optimization efficiency 收稿日期:2016-05-17. 网络出版日期:2017-06-06. 基金项目:国家自然科学基金项目(61501186);江西省普通本科高校中 青年教师发展计划访问学者专项资金项目;江西省自然科学 基金项目( 20171BAB202001);江西省教育厅科学基金项目 (GJJ150491). 通信作者:丁青锋. E⁃mail:brandy724@ sina.com. 随着科技的进步和生产技术的发展,优化问题 几乎遍布科学研究及工程实践的各个领域,成为现 代科技不可或缺的理论基础和研究方法。 而具有 启发式和随机特性的进化算法,如遗传算法(genetic algorithm,GA) [1] 、进化规划( evolution programming, EP) [2]以及进化策略( evolution strategy,ES) [3] 具有 算法效率高、易操作以及简单通用等特点,也成为 解决现实世界中优化问题的有效工具,取得了一些 有效的成果。 但随着信息时代的快速发展以及“大 数据”的涌现,现在的科学研究以及工程实践中优 化问题通常具有规模大、复杂程度高以及包含大量 局部最优解等特点,很多优化问题并没有明确的数 学解析式,或者其本身就是非确定性多项式难题 (non⁃deterministic polynomial,NP),现有研究成果及 方法远远不能满足。 差分进化算法( differential evolution,DE) 作为 一种新型、高效的启发式并行搜索技术,通过对现 有优化方法进行大胆的扬弃,具有收敛快、控制参 数少且设置简单、优化结果稳健等优点[4] ,对进化 算法的理论和应用研究具有重要的学术意义。 但 是,标准的 DE 算法也具有控制参数选择的压力大 以及搜索能力与开发能力相矛盾的现象,往往容易

.432 智能系统学报 第12卷 造成种群个体早熟收敛、搜索停滞等诸多问题。尤 DE算法具有非常优秀的寻优能力,大量应用 其是对于某些理论计算复杂度较高的工程难题,用 于理论研究与工程实际中,如在信号处理[6、生 标准的DE算法难以有效解决,亟待提出稳健、快速 物[)、计算机网络[)、协同中继、卫星通信o]、机 收敛以及精确寻优的改进型DE算法。目前,针对 械设计与机器人)、电力电子2-)、电力系统 某些特定问题,不少文献提出了很多改进型的DE 电磁兼容s)、图像处理16)、工业控制)、天线设 算法。但是近几年国内很少有文献系统地阐述DE 计8】、电子设计[]等领域都取得了非常显著的效 算法优化过程中存在的问题以及研究这些问题所 果。DE算法的研究最多的领域为工程、数学、计算 产生的机理,给后续的研究者造成了很大的困扰, 机科学和物理,占了研究论文总数的近70%,其他 同时也使如何选择改进算法变得困难。 所有学科占了总数的30%左右。可以看出,对DE 算法的研究主要集中在工程、数学应用领域。 1国内外研究概况 DE算法性能分析与改进研究,主要针对DE算 1.1发展历史 法两个方面的缺陷进行:1)当种群个体无法继续寻 DE算法[)是由Store和Price于1997年提出的 找最优解,停止向全局最优方向进化的现象,即收 一种基于群体差异的启发式并行搜索方法,提出的 缩停滞问题:2)种群个体失去多样性,陷入局部最 初衷是为了求解切比雪夫多项式问题。作为一种 优解的现象,即早熟收敛问题。而国内外学者对其 基于群体导向的随机搜索技术,DE算法包括初始 改进策略主要集中在以下4个方面:控制参数设置、 化、变异、交叉以及选择等操作:与其他优化算法不 进化策略选择、种群结构以及与其他优化算法混合。 同在于,DE算法的进化个体扰动是通过多个个体 目前,DE算法已拓展到多目标优化领域。文 的差分信息来体现的,如图1所示。 献[20]提出基于差分进化算法的多目标优化算法, 100 该算法在变异阶段利用多导向器代替传统的基向 量选择解决约束优化问题,另外采用非支配排序法 和二级种群求解非支配解:MO-ABC/DE算法[21]则 通过结合人工蜂群算法(artificial bee colony,ABC) 与DE算法的集体智慧解决非约束多目标优化问 题:Coelho等[22]提出一种基于截断伽马概率分布的 50 多目标DE算法用以解决变压器设计问题:Wu 等[2]提出MOSADE算法解决混合动力车中部件尺 -100 100 -50 50 100 寸与控制策略并行优化问题;Cheng等[2提出两阶 段多目标DE算法解决资源有限项目中的时间-成 图1二维差分进化算法的进化步骤 本权衡问题:为了获得目标表面噪声的非劣最优 Fig.1 The evolutional step of 2-D differential evolution 解,Rakshit等提出3种新的选择策略用以提高多目 由于DE算法在不同进化阶段个体间的差异性 标DE算法性能:文献[25]提出基于特征提取与集 会随之变化,因此不同阶段会出现不同的搜索能力 成学习技术的多目标DE算法用于生物实体提取; 和开发能力:进化初期的个体差异性较大,DE算法 Caravggi等[2结合DE算法和SPEA算法用于解决 将在较大范围内进行搜索最优解,因此这个阶段的 电磁问题。 搜索能力较强:进化末期种群趋于逐渐收敛的状 在国内,孟红云等]提出一种基于双群体搜索 态,个体间差异性较小,因此这个阶段的开发能力 机制的求解约束多目标优化问题的DE算法;毕晓 较强。正是这种种群自我调节能力,从而使DE算 君等[2]通过云模型对DE算法的参数进行自适应 法具有广泛的适用能力。DE算法作为一种启发式 处理,增强算法对解的探索能力:郭俊等[]利用改 并行搜索方法,因其突出的优化性能受到越来越多 进的多目标DE算法解决铝电解多目标优化问题: 研究者的广泛关注。 严细辉等0)利用模拟退火思想改进多目标DE算 1.2研究概况 法解决以能耗、实际区间运行时间、精确停车及不 目前,DE算法已成为进化计算领域的研究热 舒适度为指标建立高速列车运行操纵多目标优化 点之一,每年都有大量的研究文献出版。从近几年 问题。 SCI收录的DE算法论文分布情况可以看出,对差分 2 差分进化算法存在的问题 进化的研究呈逐年上升的趋势,但在数量上还远不 及遗传算法及其他优化方法。 DE算法从生物进化得到启发,利用群体的优
造成种群个体早熟收敛、搜索停滞等诸多问题。 尤 其是对于某些理论计算复杂度较高的工程难题,用 标准的 DE 算法难以有效解决,亟待提出稳健、快速 收敛以及精确寻优的改进型 DE 算法。 目前,针对 某些特定问题,不少文献提出了很多改进型的 DE 算法。 但是近几年国内很少有文献系统地阐述 DE 算法优化过程中存在的问题以及研究这些问题所 产生的机理,给后续的研究者造成了很大的困扰, 同时也使如何选择改进算法变得困难。 1 国内外研究概况 1.1 发展历史 DE 算法[5]是由 Store 和 Price 于 1997 年提出的 一种基于群体差异的启发式并行搜索方法,提出的 初衷是为了求解切比雪夫多项式问题。 作为一种 基于群体导向的随机搜索技术,DE 算法包括初始 化、变异、交叉以及选择等操作;与其他优化算法不 同在于,DE 算法的进化个体扰动是通过多个个体 的差分信息来体现的,如图 1 所示。 图 1 二维差分进化算法的进化步骤 Fig.1 The evolutional step of 2⁃D differential evolution 由于 DE 算法在不同进化阶段个体间的差异性 会随之变化,因此不同阶段会出现不同的搜索能力 和开发能力:进化初期的个体差异性较大,DE 算法 将在较大范围内进行搜索最优解,因此这个阶段的 搜索能力较强;进化末期种群趋于逐渐收敛的状 态,个体间差异性较小,因此这个阶段的开发能力 较强。 正是这种种群自我调节能力,从而使 DE 算 法具有广泛的适用能力。 DE 算法作为一种启发式 并行搜索方法,因其突出的优化性能受到越来越多 研究者的广泛关注。 1.2 研究概况 目前,DE 算法已成为进化计算领域的研究热 点之一,每年都有大量的研究文献出版。 从近几年 SCI 收录的 DE 算法论文分布情况可以看出,对差分 进化的研究呈逐年上升的趋势,但在数量上还远不 及遗传算法及其他优化方法。 DE 算法具有非常优秀的寻优能力,大量应用 于理论研究与工程实际中,如在信号处理[6] 、 生 物[7] 、计算机网络[8] 、协同中继[9] 、卫星通信[10] 、机 械设计与机器人[11] 、电力电子[12-13] 、电力系统[14] 、 电磁兼容[15] 、图像处理[16] 、工业控制[17] 、天线设 计[18] 、电子设计[19] 等领域都取得了非常显著的效 果。 DE 算法的研究最多的领域为工程、数学、计算 机科学和物理,占了研究论文总数的近 70%,其他 所有学科占了总数的 30%左右。 可以看出,对 DE 算法的研究主要集中在工程、数学应用领域。 DE 算法性能分析与改进研究,主要针对 DE 算 法两个方面的缺陷进行:1)当种群个体无法继续寻 找最优解,停止向全局最优方向进化的现象,即收 缩停滞问题;2) 种群个体失去多样性,陷入局部最 优解的现象,即早熟收敛问题。 而国内外学者对其 改进策略主要集中在以下 4 个方面:控制参数设置、 进化策略选择、种群结构以及与其他优化算法混合。 目前,DE 算法已拓展到多目标优化领域。 文 献[20]提出基于差分进化算法的多目标优化算法, 该算法在变异阶段利用多导向器代替传统的基向 量选择解决约束优化问题,另外采用非支配排序法 和二级种群求解非支配解;MO⁃ABC / DE 算法[21] 则 通过结合人工蜂群算法( artificial bee colony,ABC) 与 DE 算法的集体智慧解决非约束多目标优化问 题;Coelho 等[22]提出一种基于截断伽马概率分布的 多目标 DE 算 法 用 以 解 决 变 压 器 设 计 问 题; Wu 等[23]提出 MOSADE 算法解决混合动力车中部件尺 寸与控制策略并行优化问题;Cheng 等[24] 提出两阶 段多目标 DE 算法解决资源有限项目中的时间-成 本权衡问题;为了获得目标表面噪声的非劣最优 解,Rakshit 等提出 3 种新的选择策略用以提高多目 标 DE 算法性能;文献[25]提出基于特征提取与集 成学习技术的多目标 DE 算法用于生物实体提取; Caravggi 等[26]结合 DE 算法和 SPEA 算法用于解决 电磁问题。 在国内,孟红云等[27]提出一种基于双群体搜索 机制的求解约束多目标优化问题的 DE 算法;毕晓 君等[28] 通过云模型对 DE 算法的参数进行自适应 处理,增强算法对解的探索能力;郭俊等[29] 利用改 进的多目标 DE 算法解决铝电解多目标优化问题; 严细辉等[30] 利用模拟退火思想改进多目标 DE 算 法解决以能耗、实际区间运行时间、精确停车及不 舒适度为指标建立高速列车运行操纵多目标优化 问题。 2 差分进化算法存在的问题 DE 算法从生物进化得到启发,利用群体的优 ·432· 智 能 系 统 学 报 第 12 卷

第4期 丁青锋,等:差分进化算法综述 ·433. 势以及并行分布的特点,为解决实际复杂优化问题 大[3]:但种群规模N。过大则会降低找到正确搜索 提供了一种可行途径。但算法中涉及的各种控制 方向的可能性[3) 参数的设置以及进化策略的选择通常都是依据经 2)控制参数。文献[34]指出,种群个体多样性 验确定的,缺乏理论的分析和指导,因此在进行各 的丧失是引发种群早熟的直接诱因。为保持种群 种实际复杂问题优化时易陷入局部最优,出现早熟 多样性,控制参数设置是否合适就显得尤为重要。 收敛或者搜索停滞等现象[3) 其中收缩因子F需要保持一定的变化范围:交叉因 2.1差分进化算法的早熟收敛问题 子CR的大小决定种群个体中元素被替代的程度: DE算法通常是一种在搜索空间内有效的搜索 较小的CR值将造成种群的多样性变化不显著,搜 算法。其中控制参数的设置与进化策略的选择是 索速度也将变慢:较大的CR值意味着种群多样性 决定算法性能好坏的关键,一旦选择不当,往往容 更好,但不利于算法的开发能力,因此算法的收敛 易造成进化种群过早地失去多样性,使种群个体集 性能将会受到影响[3] 中到某一局部最优点,导致种群整体早熟收敛,无 3)进化策略:搜索能力与开发能力是差分进化 法实现向全局最优进化[32】,从图2中可以清楚地看 算法性能重要的标准。其中搜索能力推动在更大 出其全局最优解及局部最优解的分布。一旦进化 范围搜索,从而使候选解具有多样性,因此可提高 个体收敛到局部最优解,新生个体很难获得更优 找到全局最优解的可能性,但搜索能力过强则易导 解,进而出现早熟收敛的情况。 致搜索停滞:开发能力推动在局部最优解附近的搜 索,因此有利于收敛,但开发能力过强则易导致早 ×10 熟收敛36]。进化策略的选择是决定差分进化算法 搜索能力与开发能力平衡的关键,不同的进化策略 3 2 表现出不同的搜索与开发能力的倾向。不同的变 异和交叉策略对算法的收敛性能有不同的影响。 0 针对上述进化种群早熟收敛的问题,很多学者 提出了多种改进的方法,通过设置合适参数和选择 2 恰当的进化策略,以希望在算法有效性(候选解的 质量)和效率(收敛速度)之间达到平衡,主要手段 (a)多峰函数 包括:控制参数调节[7-9]、局部优化[o]和混合其他 优化算法41-。其中,局部优化通过在搜索到的最 优解附近进行精细搜索,最终实现优化结果精确度 局部最优解 的提高。然而,自适应变异策略一方面可以赋予进 化算法快速精确地定位局部最优解,另一方面也是 局部最优解 易陷入早熟收敛从而导致寻优失败[)]。提高种群 全局最优图 的多样性可以增强算法搜索大空间的能力,避免早 熟收敛问题的发生;然而,增强种群多元性虽然能 搜索到更大的空间,但容易降低种群进化的收敛速 0 2 度,甚至陷入局部最优从而导致优化失败。 (b)最优解分布 算法整体收敛速度也是DE算法的一个重要指 图2多峰函数的早熟收敛 标。虽然已有不少文献提出了许多改进算法,但是 Fig.2 The premature convergence of multi-peaks function 针对某些特定问题,其优化结果往往很难令人满 影响DE算法早熟收敛的主要因素可以归纳为 意。对于一种优化算法来说,在保证一定收敛速度 以下几点: 的同时,避免算法陷入早熟收敛是一个需要平衡的 1)种群初始化及种群规模。若种群初始化分 难题。因此,差分进化算法仍需要改进,以适应更 布在解空间的局部区域,则易造成算法收缩空间受 多的优化环境。 限。如果进化种群过小,容易造成有效等位基因的 2.2差分进化算法的搜索停滞问题 缺失,从而降低生成具有竞争力的个体可能性进而 假如进化算法变异、交叉后所产生的进化种群 增加种群早熟收敛的可能性)。为了保持足够的 个体比原种群个体的适应度差,则进化个体的更新 种群多样性,避免早熟收敛,种群规模V。应该足够 机制就陷入停顿,即算法的进一步迭代很难产生适 应度更好的个体,最终导致搜索停滞现象的发生
势以及并行分布的特点,为解决实际复杂优化问题 提供了一种可行途径。 但算法中涉及的各种控制 参数的设置以及进化策略的选择通常都是依据经 验确定的,缺乏理论的分析和指导,因此在进行各 种实际复杂问题优化时易陷入局部最优,出现早熟 收敛或者搜索停滞等现象[31] 。 2.1 差分进化算法的早熟收敛问题 DE 算法通常是一种在搜索空间内有效的搜索 算法。 其中控制参数的设置与进化策略的选择是 决定算法性能好坏的关键,一旦选择不当,往往容 易造成进化种群过早地失去多样性,使种群个体集 中到某一局部最优点,导致种群整体早熟收敛,无 法实现向全局最优进化[32] ,从图 2 中可以清楚地看 出其全局最优解及局部最优解的分布。 一旦进化 个体收敛到局部最优解,新生个体很难获得更优 解,进而出现早熟收敛的情况。 (a)多峰函数 (b)最优解分布 图 2 多峰函数的早熟收敛 Fig.2 The premature convergence of multi⁃peaks function 影响 DE 算法早熟收敛的主要因素可以归纳为 以下几点: 1)种群初始化及种群规模。 若种群初始化分 布在解空间的局部区域,则易造成算法收缩空间受 限。 如果进化种群过小,容易造成有效等位基因的 缺失,从而降低生成具有竞争力的个体可能性进而 增加种群早熟收敛的可能性[31] 。 为了保持足够的 种群多样性,避免早熟收敛,种群规模 NP 应该足够 大[33] ;但种群规模 NP 过大则会降低找到正确搜索 方向的可能性[31] 。 2)控制参数。 文献[34]指出,种群个体多样性 的丧失是引发种群早熟的直接诱因。 为保持种群 多样性,控制参数设置是否合适就显得尤为重要。 其中收缩因子 F 需要保持一定的变化范围;交叉因 子 CR 的大小决定种群个体中元素被替代的程度: 较小的 CR 值将造成种群的多样性变化不显著,搜 索速度也将变慢;较大的 CR 值意味着种群多样性 更好,但不利于算法的开发能力,因此算法的收敛 性能将会受到影响[35] 。 3)进化策略:搜索能力与开发能力是差分进化 算法性能重要的标准。 其中搜索能力推动在更大 范围搜索,从而使候选解具有多样性,因此可提高 找到全局最优解的可能性,但搜索能力过强则易导 致搜索停滞;开发能力推动在局部最优解附近的搜 索,因此有利于收敛,但开发能力过强则易导致早 熟收敛[36] 。 进化策略的选择是决定差分进化算法 搜索能力与开发能力平衡的关键,不同的进化策略 表现出不同的搜索与开发能力的倾向。 不同的变 异和交叉策略对算法的收敛性能有不同的影响。 针对上述进化种群早熟收敛的问题,很多学者 提出了多种改进的方法,通过设置合适参数和选择 恰当的进化策略,以希望在算法有效性(候选解的 质量)和效率(收敛速度)之间达到平衡,主要手段 包括:控制参数调节[37-39] 、局部优化[40] 和混合其他 优化算法[41-42] 。 其中,局部优化通过在搜索到的最 优解附近进行精细搜索,最终实现优化结果精确度 的提高。 然而,自适应变异策略一方面可以赋予进 化算法快速精确地定位局部最优解,另一方面也是 易陷入早熟收敛从而导致寻优失败[43] 。 提高种群 的多样性可以增强算法搜索大空间的能力,避免早 熟收敛问题的发生;然而,增强种群多元性虽然能 搜索到更大的空间,但容易降低种群进化的收敛速 度,甚至陷入局部最优从而导致优化失败。 算法整体收敛速度也是 DE 算法的一个重要指 标。 虽然已有不少文献提出了许多改进算法,但是 针对某些特定问题,其优化结果往往很难令人满 意。 对于一种优化算法来说,在保证一定收敛速度 的同时,避免算法陷入早熟收敛是一个需要平衡的 难题。 因此,差分进化算法仍需要改进,以适应更 多的优化环境。 2.2 差分进化算法的搜索停滞问题 假如进化算法变异、交叉后所产生的进化种群 个体比原种群个体的适应度差,则进化个体的更新 机制就陷入停顿,即算法的进一步迭代很难产生适 应度更好的个体,最终导致搜索停滞现象的发生。 第 4 期 丁青锋,等:差分进化算法综述 ·433·

·434 智能系统学报 第12卷 如图3所示,若6个候选个体的适应度函数值皆劣 数,初值为0,i=1,2,…,Np。若{nu.c}持续增加,则 于个体A,则个体A将保留到下一代。若个体B、C、 说明DE算法无法为目标个体i产生极值解。 D也重复个体A的情况,意味着下一代种群与现有 克服进化算法搜索停滞的一般方法是在算法 种群相同,即出现搜索停滞的情况。因此虽然种群 中引入能够在整个解空间中进行广泛搜索的策略, 仍然保持多样性,但无法再进一步收敛。 另外通过jitter/dither扰动技术,也可以降低搜索停 15f 滞出现的概率[]。在不改变种群规模的情况下,文 献[46]指出,通过收缩因子F和增大交叉因子CR 可以增加种群个体的多样性:文献[33]指出,通过 5 设置收缩因子F在进化过程中为随机数,可以有效 ●C A 增加候选个体的数量,实现算法稳定性的提高。 B 也有学者4]为平衡算法集中搜索与多样化搜 -5 ●D 索策略之间的矛盾,提出外在的种群多样化测度方 法,根据群体多样化测度值在算法的不同搜索阶段 -10 使用不同搜索策略,从而克服搜索停滞的缺陷。但 -15 群体多样化测度方法通常是针对某一算法构造的, -15 -10 -5 0 5 1015 缺乏对搜索停滞的起因、表现特征深入系统的研 (a)现有种群 究,因此具有较大的局限性。 在研究DE算法大量文献中,很少提及搜索停 15 滞问题产生机理。文献[48]进一步对群体优化算 10 法的搜索机理进行探讨,针对集中化搜索与多样化 搜索对进化停滞的影响进行了研究,从而证明了集 5 中化搜索策略具有将候选解趋于单一化的特点,是 A 0 导致算法搜索停滞的主要原因:而多样化搜索策略 00 则具有将候选解泛化的特点,即从任何一个候选解 -5 中o 可以搜索到整个解空间的任意一点,但其缺点是使 -10 算法不收敛。文献[44]指出,无法确切地发现搜素 停滞的原理,但是通过增加种群个体的多样性及规 -15 -15-10-5 051015 模可以在一定程度上降低该问题出现的概率。 (b)个体A的候选个体 3差分进化算法的改进策略 图3差分进化算法搜索停滞 针对DE算法的理论研究主要集中在如何提高 Fig.3 Search stagnation of DE 算法的寻优能力、收敛速度以及克服启发式算法常 DE算法出现搜索停滞具有以下两个特征4: 见的早熟收敛以及搜索停滞等缺陷方面。近年来, 1)种群个体不收敛:2)个体进化更新机制失效。 研究人员从多个角度不断改进算法以适应更为复 当DE算法搜索停滞发生时,停滞特征1)可以 杂的优化问题和满足更高的求解质量,改进算法大 用第G代的目标个体与其重心之间的平均距离来 致分为控制参数设置、差分策略选择、种群结构以 描述: 及与其他最优化算法混合等四大类。 de=(1/Np)∑Ixc-el (1) 1)控制参数 式中:&=(1/N,)∑”xe为标个体的重心。若 DE算法的控制参数主要有种群规模Vp、缩放 因子F以及交叉概率CR。如果参数选择不恰当 平均距离没有下降到一个很小值,则意味着种群未 可能会由于过度强调搜索能力导致算法搜索停滞 收敛到一个极值点。 或者过度强调开发能力导致算法早熟收敛。其中 DE算法发生搜索停滞时的特征2)可以用第G 种群规模主要影响种群的多样性以及收敛速度:增 代目标个体最近连续未更新次数来描述: 大N。可以提高种群的多样性,但同时降低种群的 (0,fu.c)≤fx.c) nui.G+1= (2) 收敛速度:减小N可以提高收敛速度,但易导致早 (n.c+1,其他 熟收敛。缩放因子F主要影响搜索步长:增大F可 式中:n.c为第G代目标个体i未最近连续更新次 以增加算法的搜索范围,提高种群多样性但同时消
如图 3 所示,若 6 个候选个体的适应度函数值皆劣 于个体 A,则个体 A 将保留到下一代。 若个体 B、C、 D 也重复个体 A 的情况,意味着下一代种群与现有 种群相同,即出现搜索停滞的情况。 因此虽然种群 仍然保持多样性,但无法再进一步收敛。 (a) 现有种群 (b)个体 A 的候选个体 图 3 差分进化算法搜索停滞 Fig.3 Search stagnation of DE DE 算法出现搜索停滞具有以下两个特征[44] : 1)种群个体不收敛;2)个体进化更新机制失效。 当 DE 算法搜索停滞发生时,停滞特征 1)可以 用第 G 代的目标个体与其重心之间的平均距离来 描述: dG = (1 / NP )∑ NP 1 ‖xi,G - x - G‖ (1) 式中: x - G = (1 / NP )∑ NP 1 xi,G 为目标个体的重心。 若 平均距离没有下降到一个很小值,则意味着种群未 收敛到一个极值点。 DE 算法发生搜索停滞时的特征 2)可以用第 G 代目标个体最近连续未更新次数来描述: nui,G+1 = 0, f(ui,G ) ≤ f(xi,G ) ni,G { + 1, 其他 (2) 式中:nui,G为第 G 代目标个体 i 未最近连续更新次 数,初值为 0,i = 1,2,…,NP 。 若 nui,G { }持续增加,则 说明 DE 算法无法为目标个体 i 产生极值解。 克服进化算法搜索停滞的一般方法是在算法 中引入能够在整个解空间中进行广泛搜索的策略, 另外通过 jitter/ dither 扰动技术,也可以降低搜索停 滞出现的概率[45] 。 在不改变种群规模的情况下,文 献[46]指出,通过收缩因子 F 和增大交叉因子 CR 可以增加种群个体的多样性;文献[33] 指出,通过 设置收缩因子 F 在进化过程中为随机数,可以有效 增加候选个体的数量,实现算法稳定性的提高。 也有学者[47] 为平衡算法集中搜索与多样化搜 索策略之间的矛盾,提出外在的种群多样化测度方 法,根据群体多样化测度值在算法的不同搜索阶段 使用不同搜索策略,从而克服搜索停滞的缺陷。 但 群体多样化测度方法通常是针对某一算法构造的, 缺乏对搜索停滞的起因、表现特征深入系统的研 究,因此具有较大的局限性。 在研究 DE 算法大量文献中,很少提及搜索停 滞问题产生机理。 文献[48] 进一步对群体优化算 法的搜索机理进行探讨,针对集中化搜索与多样化 搜索对进化停滞的影响进行了研究,从而证明了集 中化搜索策略具有将候选解趋于单一化的特点,是 导致算法搜索停滞的主要原因;而多样化搜索策略 则具有将候选解泛化的特点,即从任何一个候选解 可以搜索到整个解空间的任意一点,但其缺点是使 算法不收敛。 文献[44]指出,无法确切地发现搜素 停滞的原理,但是通过增加种群个体的多样性及规 模可以在一定程度上降低该问题出现的概率。 3 差分进化算法的改进策略 针对 DE 算法的理论研究主要集中在如何提高 算法的寻优能力、收敛速度以及克服启发式算法常 见的早熟收敛以及搜索停滞等缺陷方面。 近年来, 研究人员从多个角度不断改进算法以适应更为复 杂的优化问题和满足更高的求解质量,改进算法大 致分为控制参数设置、差分策略选择、种群结构以 及与其他最优化算法混合等四大类。 1)控制参数 DE 算法的控制参数主要有种群规模 NP 、缩放 因子 F 以及交叉概率 CR。 如果参数选择不恰当, 可能会由于过度强调搜索能力导致算法搜索停滞 或者过度强调开发能力导致算法早熟收敛。 其中 种群规模主要影响种群的多样性以及收敛速度:增 大 NP 可以提高种群的多样性,但同时降低种群的 收敛速度;减小 NP 可以提高收敛速度,但易导致早 熟收敛。 缩放因子 F 主要影响搜索步长:增大 F 可 以增加算法的搜索范围,提高种群多样性但同时消 ·434· 智 能 系 统 学 报 第 12 卷
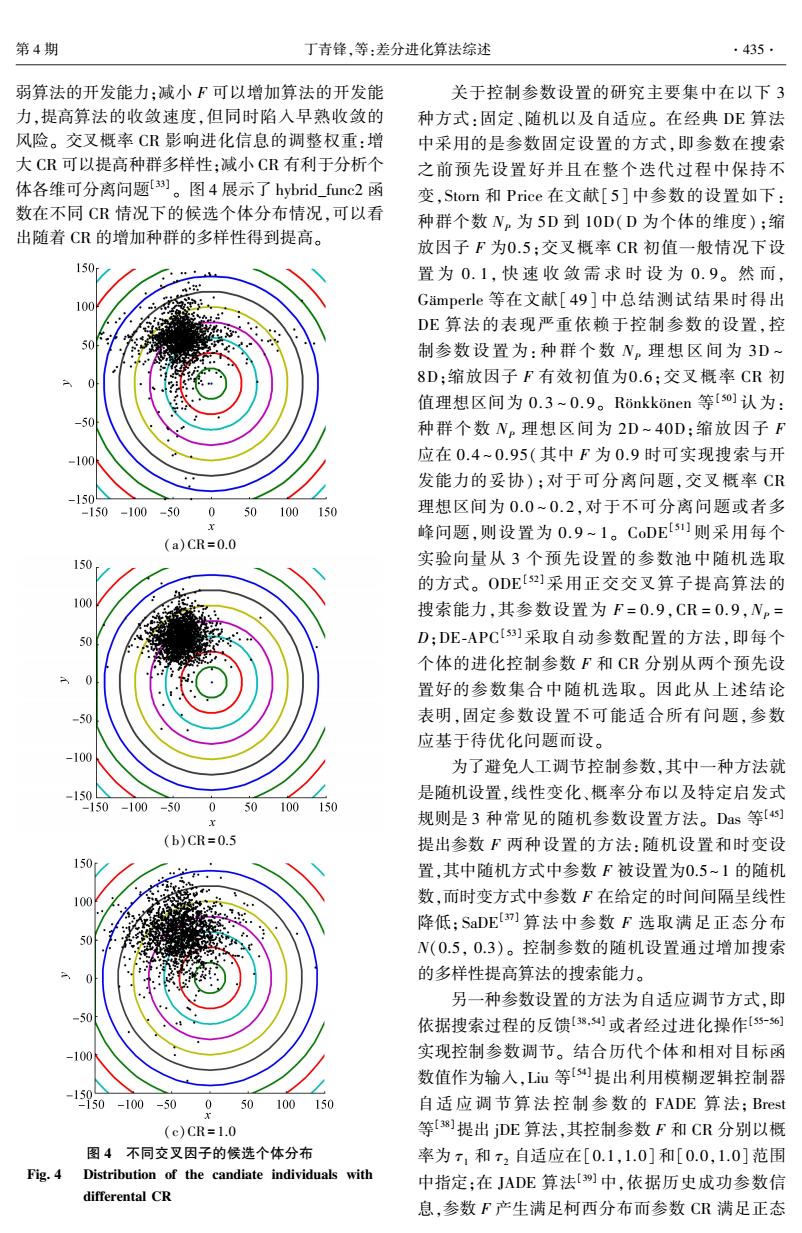
第4期 丁青锋,等:差分进化算法综述 ·435. 弱算法的开发能力:减小F可以增加算法的开发能 关于控制参数设置的研究主要集中在以下3 力,提高算法的收敛速度,但同时陷入早熟收敛的 种方式:固定、随机以及自适应。在经典DE算法 风险。交叉概率CR影响进化信息的调整权重:增 中采用的是参数固定设置的方式,即参数在搜索 大CR可以提高种群多样性:减小CR有利于分析个 之前预先设置好并且在整个迭代过程中保持不 体各维可分离问题划。图4展示了hybrid_func2函 变,Stom和Price在文献[5]中参数的设置如下: 数在不同CR情况下的候选个体分布情况,可以看 种群个数Np为5D到10D(D为个体的维度):缩 出随着CR的增加种群的多样性得到提高。 放因子F为0.5;交叉概率CR初值一般情况下设 150 置为0.1,快速收敛需求时设为0.9。然而, 100 Gamperle等在文献[49]中总结测试结果时得出 DE算法的表现严重依赖于控制参数的设置,控 制参数设置为:种群个数N。理想区间为3D~ 8D:缩放因子F有效初值为0.6;交叉概率CR初 值理想区间为0.3~0.9。Ronkkonen等[s0o]认为: 种群个数N。理想区间为2D~40D:缩放因子F 应在0.4~0.95(其中F为0.9时可实现搜索与开 发能力的妥协);对于可分离问题,交叉概率CR -150 -150-100 -50 050100150 理想区间为0.0~0.2,对于不可分离问题或者多 ” 峰问题,则设置为0.9~1。CoDE's1则采用每个 (a)CR=0.0 150 实验向量从3个预先设置的参数池中随机选取 的方式。ODE[s]采用正交交叉算子提高算法的 100 搜索能力,其参数设置为F=0.9,CR=0.9,Np= 50 D:DE-APCs3]采取自动参数配置的方法,即每个 个体的进化控制参数F和CR分别从两个预先设 置好的参数集合中随机选取。因此从上述结论 -50 表明,固定参数设置不可能适合所有问题,参数 应基于待优化问题而设。 -100 为了避免人工调节控制参数,其中一种方法就 -150 是随机设置,线性变化、概率分布以及特定启发式 150-100-50050100150 规则是3种常见的随机参数设置方法。Das等[4s) (b)CR=0.5 提出参数F两种设置的方法:随机设置和时变设 150r 置,其中随机方式中参数F被设置为0.5~1的随机 100 数,而时变方式中参数F在给定的时间间隔呈线性 降低:SaDE算法中参数F选取满足正态分布 N(0.5,0.3)。控制参数的随机设置通过增加搜索 的多样性提高算法的搜索能力。 另一种参数设置的方法为自适应调节方式,即 依据搜索过程的反馈8,]或者经过进化操作s5-s6 100 实现控制参数调节。结合历代个体和相对目标函 数值作为输入,Lu等s提出利用模糊逻辑控制器 -150-100-50 050100150 自适应调节算法控制参数的FADE算法;Brest (c)CR=1.0 等3]提出DE算法,其控制参数F和CR分别以概 图4不同交叉因子的候选个体分布 率为7,和72自适应在[0.1,1.0]和[0.0,1.0]范围 Fig.4 Distribution of the candiate individuals with 中指定:在JADE算法[3]中,依据历史成功参数信 differental CR 息,参数F产生满足柯西分布而参数CR满足正态
弱算法的开发能力;减小 F 可以增加算法的开发能 力,提高算法的收敛速度,但同时陷入早熟收敛的 风险。 交叉概率 CR 影响进化信息的调整权重:增 大 CR 可以提高种群多样性;减小 CR 有利于分析个 体各维可分离问题[33] 。 图 4 展示了 hybrid_func2 函 数在不同 CR 情况下的候选个体分布情况,可以看 出随着 CR 的增加种群的多样性得到提高。 (a)CR= 0.0 (b)CR= 0.5 (c)CR= 1.0 图 4 不同交叉因子的候选个体分布 Fig. 4 Distribution of the candiate individuals with differental CR 关于控制参数设置的研究主要集中在以下 3 种方式:固定、随机以及自适应。 在经典 DE 算法 中采用的是参数固定设置的方式,即参数在搜索 之前预先设置好并且在整个迭代过程中保持不 变,Storn 和 Price 在文献[ 5] 中参数的设置如下: 种群个数 NP 为 5D 到 10D(D 为个体的维度) ;缩 放因子 F 为0.5;交叉概率 CR 初值一般情况下设 置 为 0. 1, 快 速 收 敛 需 求 时 设 为 0. 9。 然 而, Gämperle 等在文献[ 49] 中总结测试结果时得出 DE 算法的表现严重依赖于控制参数的设置,控 制参数 设 置 为: 种 群 个 数 NP 理 想 区 间 为 3D ~ 8D;缩放因子 F 有效初值为0.6;交叉概率 CR 初 值理想区间为 0. 3 ~ 0. 9。 Rönkkönen 等[ 50] 认为: 种群个数 NP 理想区间为 2D ~ 40D;缩放因子 F 应在 0.4 ~ 0.95(其中 F 为 0.9 时可实现搜索与开 发能力的妥协) ;对于可分离问题,交叉概率 CR 理想区间为 0.0 ~ 0. 2,对于不可分离问题或者多 峰问题,则设置为 0. 9 ~ 1。 CoDE [ 51] 则采用每个 实验向量从 3 个预先设置的参数池中随机选取 的方式。 ODE [ 52] 采用正交交叉算子提高算法的 搜索能力,其参数设置为 F = 0. 9,CR = 0. 9,NP = D;DE⁃APC [ 53] 采取自动参数配置的方法,即每个 个体的进化控制参数 F 和 CR 分别从两个预先设 置好的参数集合中随机选取。 因此从上述结论 表明,固定参数设置不可能适合所有问题,参数 应基于待优化问题而设。 为了避免人工调节控制参数,其中一种方法就 是随机设置,线性变化、概率分布以及特定启发式 规则是 3 种常见的随机参数设置方法。 Das 等[45] 提出参数 F 两种设置的方法:随机设置和时变设 置,其中随机方式中参数 F 被设置为0.5~ 1 的随机 数,而时变方式中参数 F 在给定的时间间隔呈线性 降低; SaDE [37] 算法中参数 F 选取满足正态分布 N(0.5, 0.3)。 控制参数的随机设置通过增加搜索 的多样性提高算法的搜索能力。 另一种参数设置的方法为自适应调节方式,即 依据搜索过程的反馈[38,54] 或者经过进化操作[55-56] 实现控制参数调节。 结合历代个体和相对目标函 数值作为输入,Liu 等[54] 提出利用模糊逻辑控制器 自适 应 调 节 算 法 控 制 参 数 的 FADE 算 法; Brest 等[38]提出 jDE 算法,其控制参数 F 和 CR 分别以概 率为 τ1 和 τ2 自适应在[0.1,1.0]和[0.0,1.0]范围 中指定;在 JADE 算法[39] 中,依据历史成功参数信 息,参数 F 产生满足柯西分布而参数 CR 满足正态 第 4 期 丁青锋,等:差分进化算法综述 ·435·