
第三章 单纯形法 这在应用 中很有价 值 定理9在LP问题的典式(1b)~(3b)中,如木一应 数满足最优准则o,≤0(j=m+1,,n),且其中有一 个o=0(m+1≤k≤n),则该LP问题有无穷多个 最优解。 定理10 在LP问题的典式(1b)~(3b)中,如果有某 个非基变量的检验数ok>0(m+1≤k≤n),且有 ak≤0(i=1,2,.,m) 即 P≤0 则该LP问题解无界(无最优解)
第三章 单纯形法 定理 9 在 LP 问题的典式 (1b) ~(3b)中,如果检验 数满足最优准则 σj ≤ 0 ( j = m+1 ,…,n ),且其中有一 个 σk = 0 ( m+1 ≤ k ≤n ),则该 LP 问题有无穷多个 最优解。 这在应用 中很有价 值 定理 10 在 LP 问题的典式 (1b) ~(3b)中,如果有某 个非基变量的检验数σk > 0 ( m+1 ≤ k ≤n ),且有 ' ' a i m p ik k = 0 ( 1,2, , ) 0 即 则该 LP 问题解无界(无最优解)
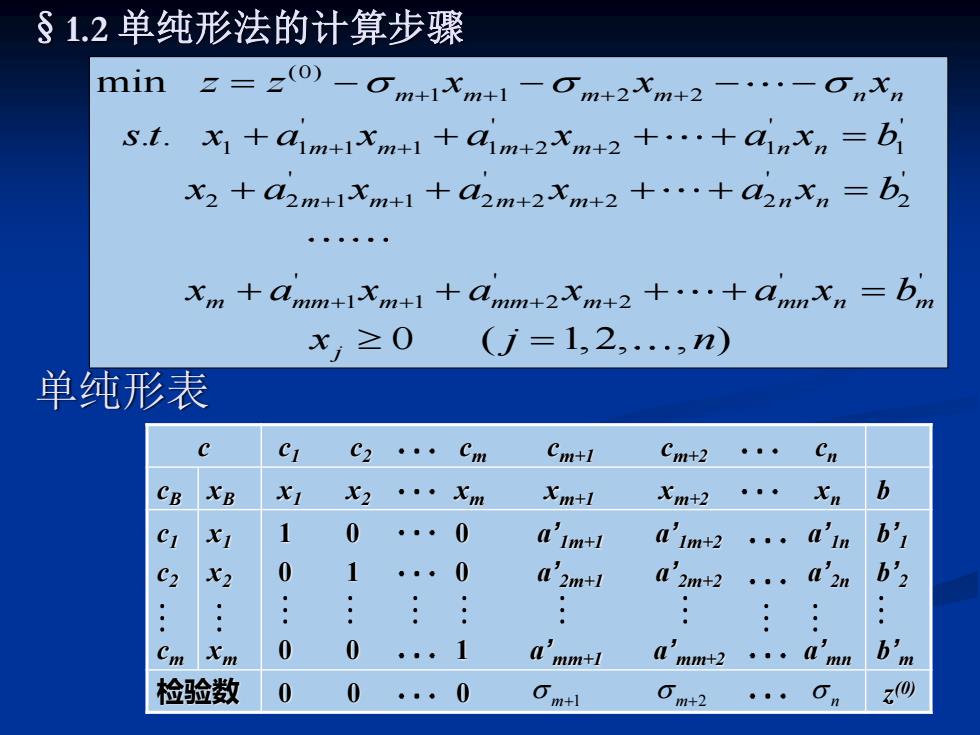
§1.2单纯形法的计算步骤 min z=2(0)-Om+1Xm+1-Om+2Xm+2-.-可nX1 S.1.x1+aim+1m+l+aim+2xm+2+..+ainxn =b X2 +a2m+1Xm++a2m+2Xm+2+...+d2nxn =b2 Xm +amm+Immm+2m2+cmnn bim x,≥0 (j=1,2,.,n) 单纯形表 C1 C2··· Cm Cm+l Cm+2 CB XB X1 X2 Xm Xm+1 Xm+2 ·。42 n b X1 1 0 0 d'im-l a'im2 a'in b'1 X2 0 1 0 a'2m+1 a'2m+2 (2n b'2 .: Xm 0 0 。。。 1 a'mm+I a'mm2 a mn b'm 检验数 0 0 。。 0 n+1 20
§1.2 单纯形法的计算步骤 单纯形表 (0) 1 1 2 2 ' ' ' ' 1 1 1 1 1 2 2 1 1 ' ' ' ' 2 2 1 1 2 2 2 2 2 ' ' ' ' 1 1 2 2 min . . 0 ( 1,2, , ) m m m m n n m m m m n n m m m m n n m mm m mm m mn n m j z z x x x s t x a x a x a x b x a x a x a x b x a x a x a x b x j n + + + + + + + + + + + + + + + + = − − − − + + + + = + + + + = + + + + = = c c1 c2 cm cm+1 cm+2 cn cB xB x1 x2 xm xm+1 xm+2 xn b c1 c2 cm x1 x2 xm 1 0 0 a’ 1m+1 a’ 1m+2 a’ 1n 0 1 0 a’ 2m+1 a’ 2m+2 a’ 2n 0 0 1 a’ mm+1 a’ mm+2 a’ mn b’ 1 b’ 2 b’ m 检验数 0 0 0 z (0) m+1 m+2 n
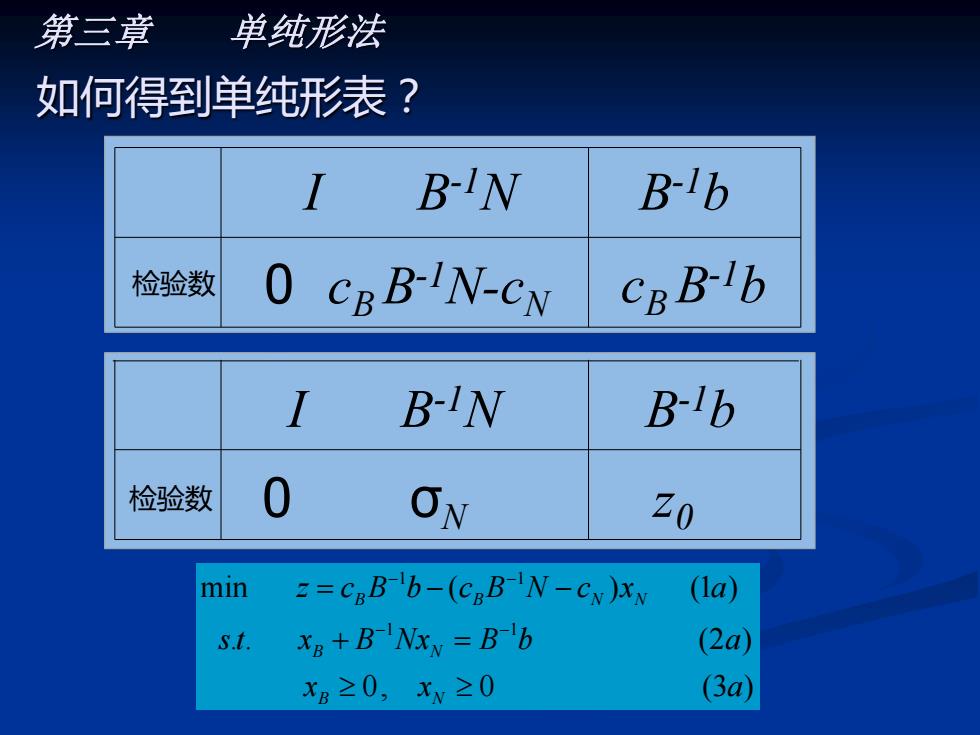
第三章 单纯形法 如何得到单纯形表? I BN B-b 检验数 0 CBBIN-CN CB B-lb B-IN B-1b 检验数 ON 20 min z=CpBb-(CpBN-CN)XN (la) s.t. X8+B Nxy =Bb (2a xB≥0,xv≥0 (3a
第三章 单纯形法 如何得到单纯形表? 1 1 1 1 min ( ) (1 ) . . (2 ) 0, 0 (3 ) B B N N B N B N z c B b c B N c x a s t x B Nx B b a x x a − − − − = − − + = -c A b 检验数 0 B-1b cB B-1b z0 I B-1N B-1b 0 σN 检验数 B N -cB -cN I B-1N 0 cB B-1N-cN