
Chapter 6 Digital Filter Structures
Chapter 6 Digital Filter Structures
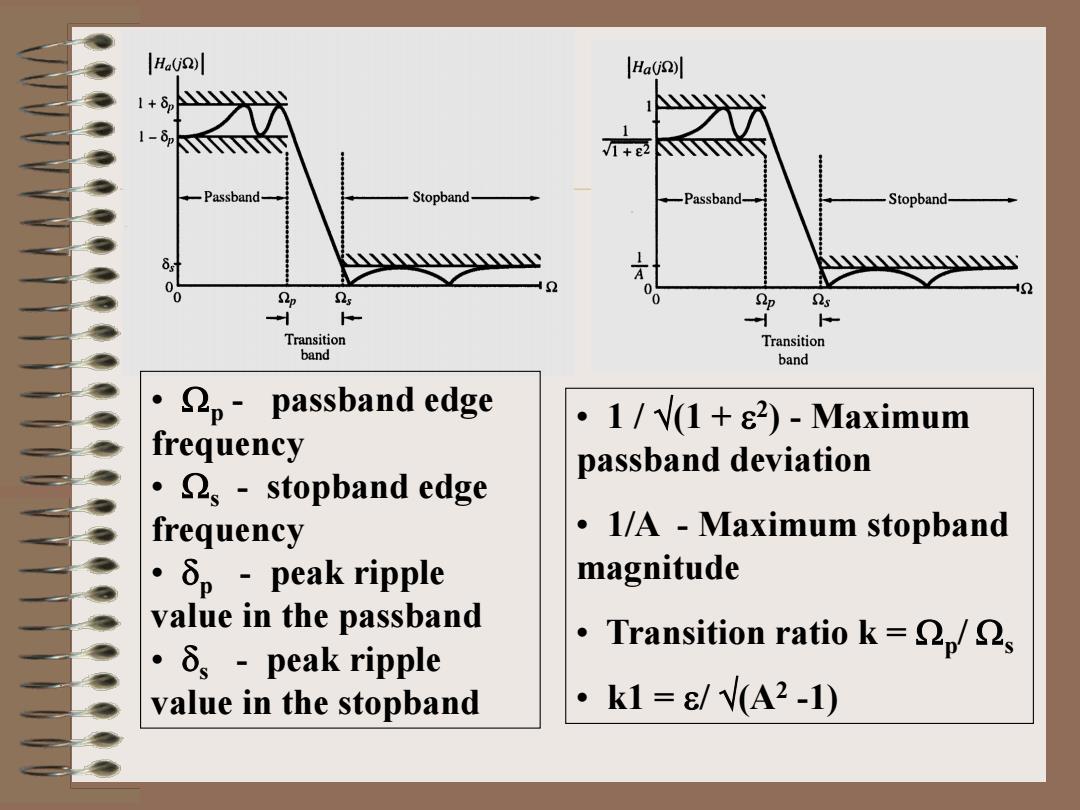
Ha() Ha() 1+δ 1+e2 -Passband- Stopband- Passband- Stopband- 2 p Qs 0 s - Transition Transition band band ·2p-passband edge ·1/V(1+ε2)-Maximum frequency passband deviation ·2s-stopband edge frequency 1/A Maximum stopband ·δp-peak ripple magnitude value in the passband ·δs-peak ripple Transition ratio k=p/s value in the stopband k1=ε/V(A2-1)
• 1 / √(1 + ε2) - Maximum passband deviation • 1/A - Maximum stopband magnitude • Transition ratio k = Ωp/ Ωs • k1 = ε/ √(A2 -1) • Ωp - passband edge frequency • Ωs - stopband edge frequency • δp - peak ripple value in the passband • δs - peak ripple value in the stopband
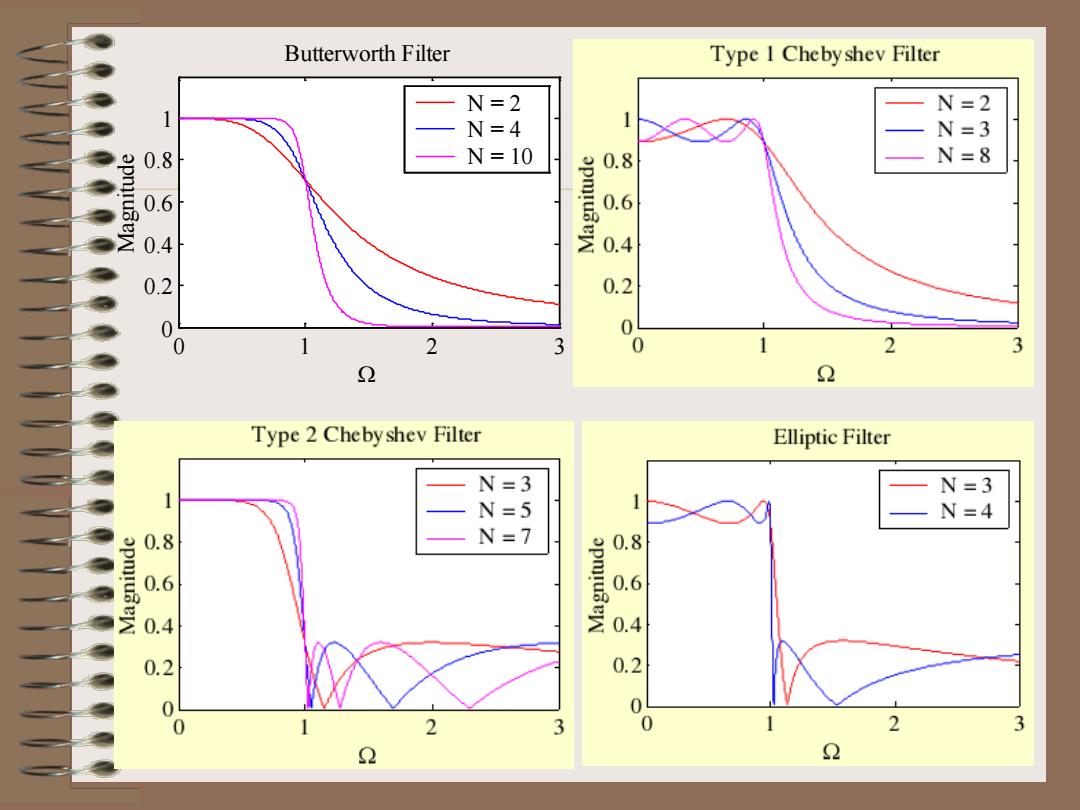
Butterworth Filter Type 1 Chebyshev Filter N=2 N=2 N=4 N=3 N=10 0.8 N=8 0.6 0.4 0.2 0.2 0 2 3 0 2 2 2 Type 2 Cheby shev Filter Elliptic Filter N=3 N=3 N=5 N=4 0.8 N=7 0.8 opmuew 0.6 0.6 0.4 0.4 0.2 0.2 0 2 3 0 2 3
0 1 2 3 0 0.2 0.4 0.6 0.81 Ω Magnitude Butterworth Filter N = 2 N = 4 N = 10

§6.1 Introduction The convolution sum description of an LTI discrete-time system can,in principle,be used to implement the system For an IIR finite-dimensional system this approach is not practical as here the impulse response is of infinite length However,a direct implementation of the IIR finite-dimensional system is practical
• The convolution sum description of an LTI discrete-time system can, in principle, be used to implement the system • For an IIR finite-dimensional system this approach is not practical as here the impulse response is of infinite length • However, a direct implementation of the IIR finite-dimensional system is practical §6.1 Introduction

§6.l.1 Block Diagram Representation In the time domain,the input-output relations of an LTI digital filter is given by the convolution sum Hm=∑-hMk]n-k] or,by the linear constant coefficient difference equation [m=-∑1d[n-]+∑0Pkx[n-]
§6.1.1 Block Diagram Representation • In the time domain, the input-output relations of an LTI digital filter is given by the convolution sum ∑∞ =−∞ = − k y[n] h[k] x[n k] ∑ = ∑ = = − − + − M k k N k k y n d y n k p x n k 1 0 [ ] [ ] [ ] or, by the linear constant coefficient difference equation