
5.1.3解的特性讨论 电子科技大学计算电磁学及其应用团队,CEMLAB ab 1958 B(k。p)的形式需根据实际物理问题确定 Jn(k.p)类似于cos(k.p) 驻波振荡特性 Nn(k.p)类似于sin(k。p) 驻波振荡特性 H四(k。p)类似于e,°(-p方向行波,内行波) H(k。p)类似于e,°(p方向行波,外行波) HO(kP)=J(keP)+jN.(kP) HO(kp)=J.(kP)-jN.(kP) 6
Computational Electromagnetics Laboratory, UESTC 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 6
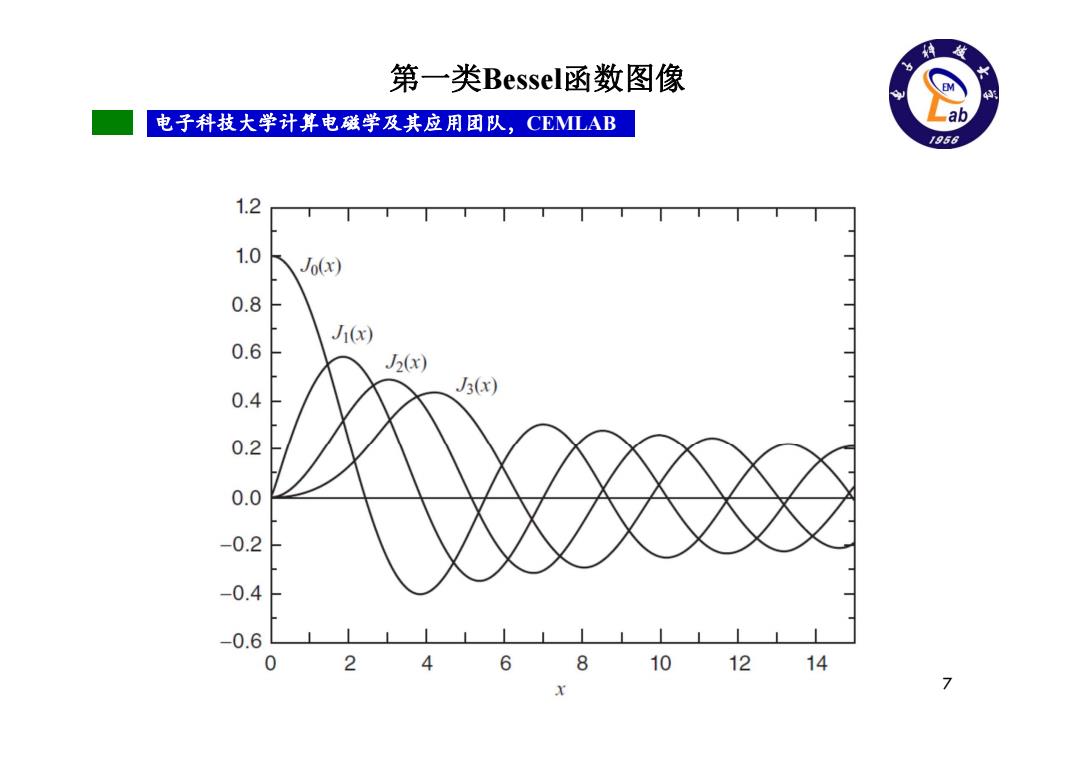
第一类Besseli函数图像 电子科技大学计算电磁学及其应用团队,CEMLAB Lab /956 1.2 1.0 Jo(x) 0.8 J(x) 0.6 J2(x) J3(x) 0.4 0.2 0.0 -0.2 -0.4 -0.6 0 2 4 6 810 12 14 7
Computational Electromagnetics Laboratory, UESTC 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 7 第一类Bessel函数图像

第二类Bessel函数图像 的 Lab 4 电子科技大学计算电磁学及其应用团队,CEMLAB /956 Yo(x) 0.5 Y(x)Yx)Y3(x) 0.0 -0.5 -1.0 0 2 4 6 8 10 12 14 x Yn(0) 三-00 8
Computational Electromagnetics Laboratory, UESTC 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 8 第二类Bessel函数图像 𝑌 0 ൌ െ∞

电子科技大学计算电磁学及其应用团队,CEMLAB ab 1958 特别地,只有J,(k。p)在p=0处为有限值,而N(k.P)在p=0处为无穷大 例:右图所示同轴传输线,计及导体内的电流, 则导体内芯及外屏蔽层中的电流密度满足亥姆 霍兹方程 V2J=joua J 记jouo.为-T2 可写为V2j+T2j=0 假设j只有:分量,方程简化为 9
Computational Electromagnetics Laboratory, UESTC 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 9 r2 r 3 r1

电子科技大学计算电磁学及其应用团队,CEMLAB ab /956 10(p.()+TJ(p)-0 (Bessel方程) pop op 其解可写为 Jm(p)=CJ(Tp),0≤p≤片(导体内芯) J(p)=CH(Tp)+C,Hg2(Tp),5≤p≤5(外屏蔽层中) 其中待定系数C,C2,C,由边界条件确定。 10
Computational Electromagnetics Laboratory, UESTC 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 10 r2 r3 r1