
标准偏差 标准偏差又称均方根偏差; 标准偏差的计算分两种情况: 1.当测定次数趋于无穷大时 标准偏差:。=∑(K-}/n W为无限多次测定的平均值(总体平均值);即: lim X=u h-→∞ 当消除系统误差时,W即为真值。 2.有限测定次数 标准偏差:s=V∑(X-沙/n-) 相对标准偏差: (变异系数)CV%=S/X 2023-3-15 下页 返回
2023-3-15 二、 标准偏差 相对标准偏差 :(变异系数)CV% = S / X 标准偏差又称均方根偏差; 标准偏差的计算分两种情况: 1.当测定次数趋于无穷大时 标准偏差 : μ 为无限多次测定 的平均值(总体平均值); 即: 当消除系统误差时,μ即为真值。 2.有限测定次数 标准偏差 : X / n 2 / 1 2 s X X n X n lim
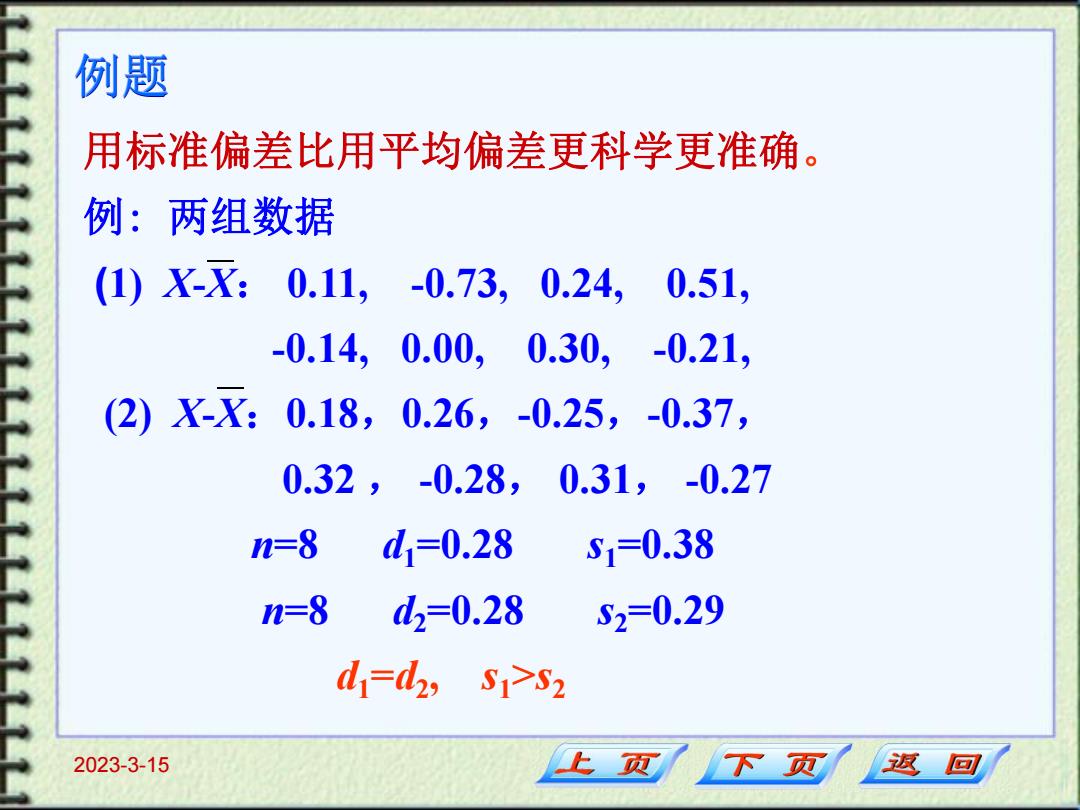
例题 用标准偏差比用平均偏差更科学更准确 例:两组数据 (1)X-X:0.11, -0.73,0.24, 0.51, -0.14, 0.00, 0.30, -0.21, (2)X-X: 0.18, 0.26,-0.25,-0.37, 0.32,-0.28, 0.31,-0.27 n=8 d1=0.28 S1=0.38 n=8 d2=0.28 52=0.29 d=d,s1-S2 2023-3-15 下页 返回
2023-3-15 例题 用标准偏差比用平均偏差更科学更准确。 例: 两组数据 (1) X-X: 0.11, -0.73, 0.24, 0.51, -0.14, 0.00, 0.30, -0.21, (2) X-X:0.18,0.26,-0.25,-0.37, 0.32 , -0.28, 0.31, -0.27 n=8 d1=0.28 s1=0.38 n=8 d2=0.28 s2=0.29 d1=d2 , s1>s2
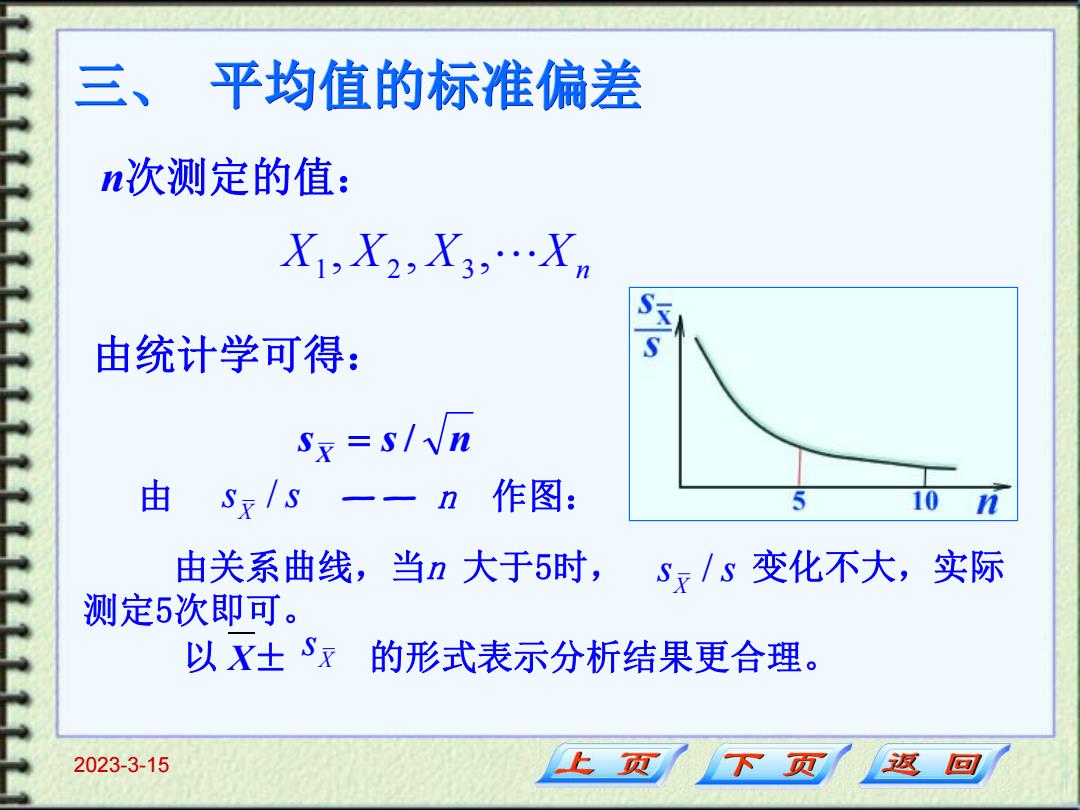
三、平均值的标准偏差 n次测定的值: X1,X2,X3,…Xm 由统计学可得: S Sx =s//n 由Sx/S 作图: 5 10 由关系曲线,当n大于5时, Sx/s变化不大,实际 测定5次即可。 以X士Sx 的形式表示分析结果更合理。 2023-3-15 页 下页 返回
2023-3-15 三、 平均值的标准偏差 n次测定的值: 由关系曲线,当n 大于5时, 变化不大,实际 测定5次即可。 以 X± 的形式表示分析结果更合理。 1 2 3 , , , X X X Xn s s n X / 由统计学可得: 由 s X / s —— n 作图: / Xs s Xs
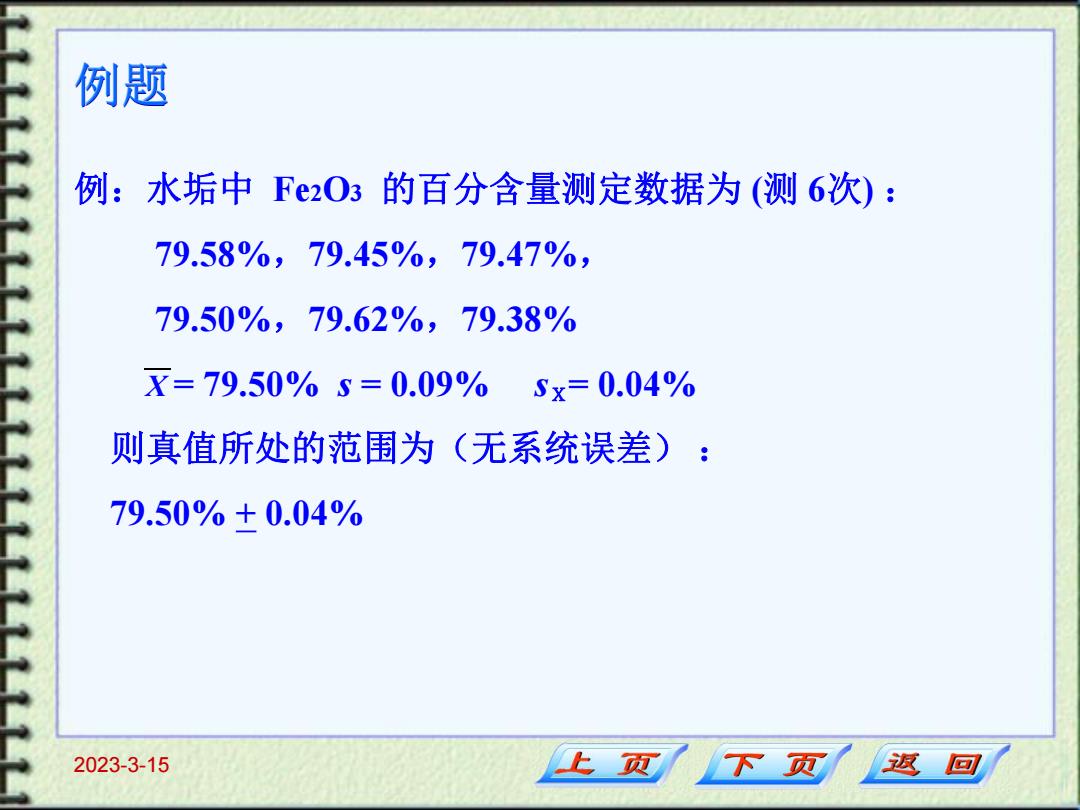
例题 例:水垢中F€2O3的百分含量测定数据为(测6次): 79.58%,79.45%,79.47%, 79.50%,79.62%,79.38% X=79.50%5=0.09% Sx=0.04% 则真值所处的范围为(无系统误差): 79.50%+0.04% 2023-3-15 上页 下页 返回
2023-3-15 例题 例:水垢中 Fe2O3 的百分含量测定数据为 (测 6次) : 79.58%,79.45%,79.47%, 79.50%,79.62%,79.38% X = 79.50% s = 0.09% sX= 0.04% 则真值所处的范围为(无系统误差) : 79.50% + 0.04%

某次测定某种溶液密度的一组数据 1.205,1.134,1.155,1.210,1.190,1.193 1.180,1.168,1.170,1.186,1.173 求标准偏差、相对标准偏差和平均值的标准偏 差?分析结果应表示为? 2023-3-15 上页 下页 返回
2023-3-15 某次测定某种溶液密度的一组数据: 1.205,1.134,1.155,1.210,1.190, 1.193 1.180,1.168,1.170,1.186,1.173 求标准偏差、相对标准偏差和平均值的标准偏 差?分析结果应表示为?