
重叠律: A十A=A A·A=A 反演律: A十B=A·B AB=A+B 吸收律 A十AB=A 4(A+B)=4 A+A·B=A+B (A+B)·(A+C○)=A+BC 其它常用恒等式 AB+AC+BC=AB+AC AB+AC+BCD=AB+AC 《》☐☐
重叠律: A + A = A A · A = A 反演律: A + B = A · B AB = A + B A A B=A B (A B)(A C)=A BC 吸收律 A AB=A A(A B)=A 其它常用恒等式 AB+AC+BC=AB + AC AB+AC+BCD=AB + AC
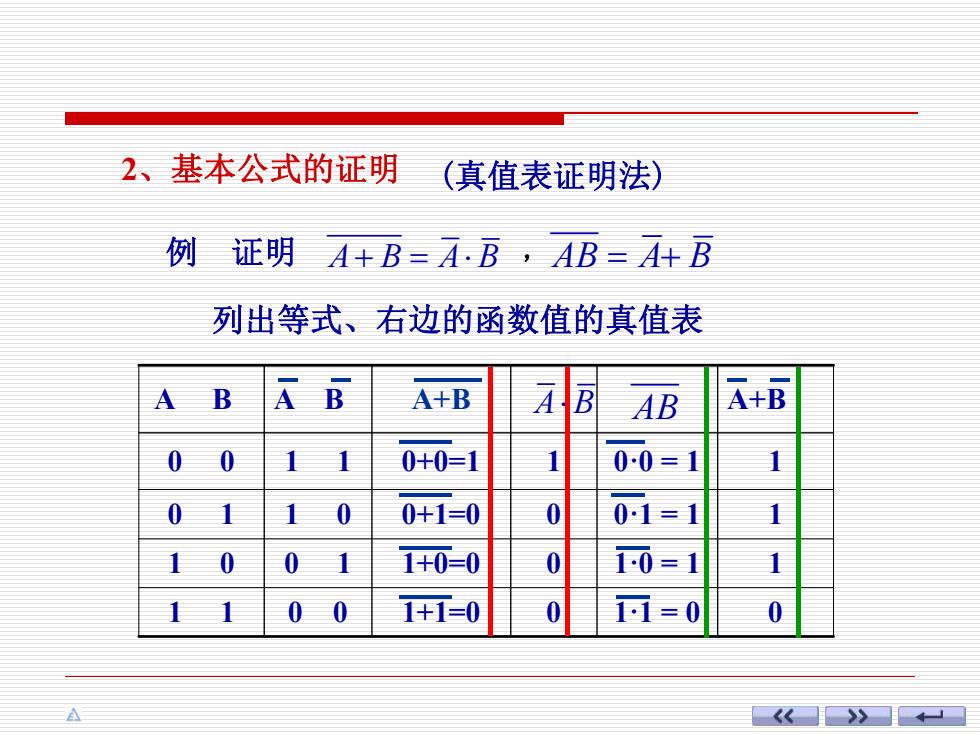
2、基本公式的证明 (真值表证明法) 例证明 A+B=AB,AB=A+B 列出等式、右边的函数值的真值表 A B A B A+B A B AB A+B 0 0+0=1 00=1 0 0+1=0 0 01=1 1+0=0 1+1=0 1=0 《》4
2、基本公式的证明 例 证明 A B A B , AB A B 列出等式、右边的函数值的真值表 (真值表证明法) 1 1 0 0 1+1=0 0 1·1 = 0 0 1 0 0 1 1+0=0 0 1·0 = 1 1 0 1 1 0 0+1=0 0 0·1 = 1 1 0 0 1 1 0+0=1 1 0·0 = 1 1 A B A B A+B A B AB A+B

2.1.2逻辑代数的基本规则 1.代入规则:在包含变量4逻辑等式中,如果用另一 个函数式代入式中所有A的位置,则等式仍然成立。这一规 则称为代入规则。 例:B(A+C=BA+BC, 用A+D代替A,得 B(A+D)+C=B(A+D)+BC=BA+BD+BC 代入规则可以扩展所有基本公式或定律的应用范围
2.1.2 逻辑代数的基本规则 1.代 入 规 则 : 在包含变量A逻辑等式中,如果用另一 个函数式代入式中所有A的位置,则等式仍然成立。这一规 则称为代入规则。 例:B (A + C) = BA+BC, 用A + D代替A,得 B [(A +D) +C ] = B(A +D) + BC = BA + BD + BC 代入规则可以扩展所有基本公式或定律的应用范围

2.反演规则: 对于任意一个逻辑表达式L,若将其中所有的与(·)换成 或(+),或(+)换成与();原变量换为反变量,反变 量换为原变量;将1换成0,0换成;则得到的结果就是原 函数的反函数。 例2.1.1试求L=AB+CD+0 的非函数 解:按照反演规则,得 L=(A+B)(C+D)·1=(A+B)(C+D) 《》☐4☐
对于任意一个逻辑表达式L,若将其中所有的与(• )换成 或(+),或(+)换成与(•);原变量换为反变量,反变 量换为原变量;将1换成0,0换成1;则得到的结果就是原 函数的反函数。 2. 反演规则: L (A B)(C D)1 (A B)(C D) 例2.1.1 试求 L AB CD 0 的非函数 解:按照反演规则,得

3.对偶规则: 对于任何逻辑函数式,若将其中的与(·)换成或(+),或(+) 换成与(·);并将1换成0,0换成1;那么,所得的新的函数式就 是L的对偶式,记作。 例:逻辑函数L=(A+B(A+C)的对偶式为 L'=AB+AC 当某个逻辑恒等式成立时,则该恒等式两侧的对偶式也相等。 这就是对偶规则。利用对偶规则,可从已知公式中得到更多的 运算公式,例如,吸收律
L AB AC 对于任何逻辑函数式,若将其中的与(• )换成或(+),或(+) 换成与(•);并将1换成0,0换成1;那么,所得的新的函数式就 是L的对偶式,记作 。 L 例: 逻辑函数 L (A B)(AC)的对偶式为 3. 对偶规则: 当某个逻辑恒等式成立时,则该恒等式两侧的对偶式也相等。 这就是对偶规则。利用对偶规则,可从已知公式中得到更多的 运算公式,例如,吸收律