
11.2.3动量矩守恒定理 1.质点动量矩守恒定律 如果作用在质点上的力对某定点(或定轴) 之矩恒等于零,则质点对该点(或该轴)的动量 矩保持不变。 2.质点系动量矩守恒定律 当外力对于某定点(或某定轴)的主矩等于 零时,质点象对于该点(或该轴)的动量矩保持 不变
1. 质点动量矩守恒定律 如果作用在质点上的力对某定点(或定轴) 之矩恒等于零,则质点对该点(或该轴)的动量 矩保持不变。 11.2.3 动量矩守恒定理 当外力对于某定点(或某定轴)的主矩等于 零时,质点系对于该点(或该轴)的动量矩保持 不变。 2. 质点系动量矩守恒定律

动量矩定理 例3高炉运送矿石的卷扬机如图。已知鼓轮的半径为R,质量 为m1,绕0轴转动。小车和矿石的总质量为2。作用在鼓轮 上的力偶矩为M,鼓轮对转轴的转动惯量为J,轨道倾角为α。 设绳质量和各处摩擦不计,求小车的加速度α。 解:以系统为研究对象,受力如图。 0 以顺时针为正,则 Lo J@+mzvR ∑Mo(Fe)=M-m,g sinaR m18 L。=∑m,E),有 由、 dt d (Jo+mvR)=M-msinaR d
例3 高炉运送矿石的卷扬机如图。已知鼓轮的半径为R,质量 为m1,绕O轴转动。小车和矿石的总质量为m2。作用在鼓轮 上的力偶矩为M,鼓轮对转轴的转动惯量为J,轨道倾角为。 设绳质量和各处摩擦不计,求小车的加速度a。 解:以系统为研究对象,受力如图。 以顺时针为正,则 LO J m2vR (e) 2 ( ) sin MO F M m g R 由 ,有 d (e) ( ) d LO mO i t F 2 2 d ( ) sin d J m vR M m g R t 动量矩定理 M O m2g N v m1g FOx FOy

动量矩定理 dv 因0= =a,于是解得 R'dt MR-m2gR'sina d= J+m,R2 若M>m2 gR sin a,则a>0,小车的加速度沿轨道向上。 必须强调的是:为使动量矩定理中各物理量的正 负号保持协调,动量矩和力矩的正负号规定必须完 全一致
因 ,于是解得 d , d v v a R t 2 2 2 2 sin J m R MR m gR a 若M>m2gR sin ,则 a>0,小车的加速度沿轨道向上。 必须强调的是:为使动量矩定理中各物理量的正 负号保持协调,动量矩和力矩的正负号规定必须完 全一致。 动量矩定理

例4水平杆AB长2a,可绕铅垂轴z转动,其两端各用铰链与长为的杆AC及 BD相连,杆端各联结质量为m的小球C和D。起初两小球用细线相连,使杆 AC与BD均为铅垂,这系统绕z轴的角速度为。如某时此细线拉断,杆AC 和BD各与铅垂线成α角。不计各杆的质量,求这时系统的角速度w。 解:以系统为研究对象,系统所受的外力有小球的 重力和轴承处的反力,这些力对转轴之矩都等于零。 所以系统对转轴的动量矩守恒,即 L1=L22 L1=2(ma0,)a=2ma2o, L:2=2m(a+lsina)@ 2ma'o =2m(a+lsina)@ a2 0三 (a+lsina)2 00 显然,此时的角速度o<oo
A B C D z 0 a a l l C A B D z a a l l 例4 水平杆AB长2a,可绕铅垂轴 z 转动,其两端各用铰链与长为l的杆AC及 BD相连,杆端各联结质量为m的小球C和D。起初两小球用细线相连,使杆 AC与BD均为铅垂,这系统绕 z 轴的角速度为0。如某时此细线拉断,杆AC 和BD各与铅垂线成 角。不计各杆的质量,求这时系统的角速度 。 解:以系统为研究对象,系统所受的外力有小球的 重力和轴承处的反力,这些力对转轴之矩都等于零。 所以系统对转轴的动量矩守恒,即 Lz1 Lz 2 2 1 0 0 2( ) 2 L z ma a ma 2 2 2 ( sin ) L z m a l 2 2 0 2ma 2m(a lsin) 2 0 2 ( sin ) a l a 显然,此时的角速度< 0
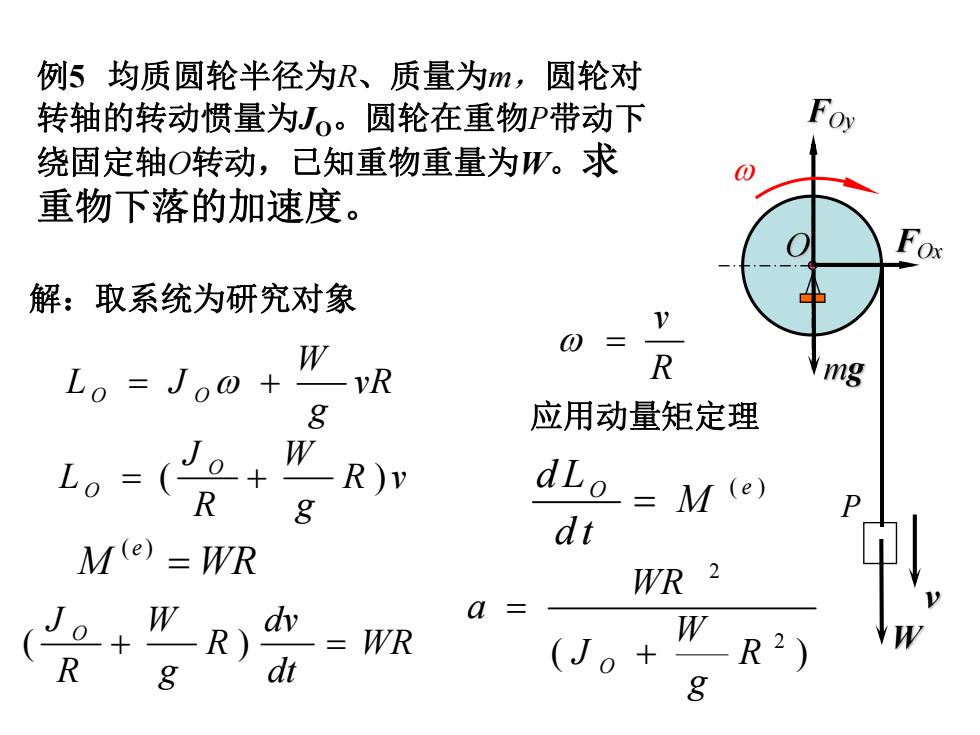
例5均质圆轮半径为R、质量为m,圆轮对 转轴的转动惯量为J。圆轮在重物P带动下 Foy 绕固定轴O转动,已知重物重量为W。求 0 重物下落的加速度。 解:取系统为研究对象 W Lo =Jo@+ -vR R mg 8 应用动量矩定理 J0 W Lo R)v R dLo=M (0) dt M(e)=WR WR 2 。+3 W dv a R) WR (J。 W 8 dt -R2) 8
解:取系统为研究对象 例5 均质圆轮半径为R、质量为m,圆轮对 转轴的转动惯量为JO。圆轮在重物P带动下 绕固定轴O转动,已知重物重量为W。求 重物下落的加速度。 vR g W L J O O M WR e ( ) R v R v g W R J L O O ( ) 应用动量矩定理 O ( e ) M d t d L WR dt dv R g W R J O ( ) ( ) 2 2 R g W J WR a O P