
远动学
运动学

运动学是研究物体运动的几何性质的科学。也 就是从几何学方面来研究物体的机械运动。运动 学的内容包括:运动方程、轨迹、速度和加速度。 学习运动学的意义:首先是为学习动力学打下 必要的基础。其次运动学本身也有独立的应用。 由于物体运动的描述是相对的。将观察者所在 的物体称为参考体,固结于参考体上的坐标条称 为参考坐标系。只有明确参考条来分析物体的运 动才有意义。 时间概念要明确:瞬时和时问间隔。 运动学所研究的力学模型为:点和则体
运动学是研究物体运动的几何性质的科学。也 就是从几何学方面来研究物体的机械运动。运动 学的内容包括:运动方程、轨迹、速度和加速度。 学习运动学的意义:首先是为学习动力学打下 必要的基础。其次运动学本身也有独立的应用。 由于物体运动的描述是相对的。将观察者所在 的物体称为参考体,固结于参考体上的坐标系称 为参考坐标系。只有明确参考系来分析物体的运 动才有意义。 时间概念要明确:瞬时和时间间隔。 运动学所研究的力学模型为:点和刚体

5点的运动学 本章将介绍研究点的运动的三种方法,即:关 径法、直角坐标法和自然法。 点运动附,在空间所占的位置随时间连续变化 而形成的曲线,称为点的运动轨迹。点的运动 可按轨迹形状分为直线运动和曲线运动。当轨 迹为圆附称为圆周运动。 表示点的位置随时间变化的规律的数学方程称 为点的运动方程。 本章研究的内容为点的运动方程、轨迹、速度 和如速度,以及它们之间的关系
5 点的运动学 本章将介绍研究点的运动的三种方法,即:矢 径法、直角坐标法和自然法。 点运动时,在空间所占的位置随时间连续变化 而形成的曲线,称为点的运动轨迹。点的运动 可按轨迹形状分为直线运动和曲线运动。当轨 迹为圆时称为圆周运动。 表示点的位置随时间变化的规律的数学方程称 为点的运动方程。 本章研究的内容为点的运动方程、轨迹、速度 和加速度,以及它们之间的关系

5.1矢量法 1.运动方程 M 选取参考系上某确定点O为坐标原点,自 点O向动点M作矢量r,称为点M相对原点O的 位置矢量,简称失径。当动点M运动时,矢径 r随时问而变化,并且是时间的单值连续函数, 即 r=r(t)
1. 运动方程 r r = ( )t 选取参考系上某确定点O为坐标原点,自 点O向动点M作矢量r,称为点M相对原点O的 位置矢量,简称矢径。当动点 M运动时,矢径 r随时间而变化,并且是时间的单值连续函数, 即 5.1 矢量法 M r O
5.1矢量法 2.速度 M A M (t什△t) B 动点的速度矢等于它的矢径对时间的一阶导数。 △ dr v=lim △t→0 t dt 动点的速度矢沿着矢径的矢端曲线的切线,即沿 动点运动轨迹的切线,并与此点运动的方向一致
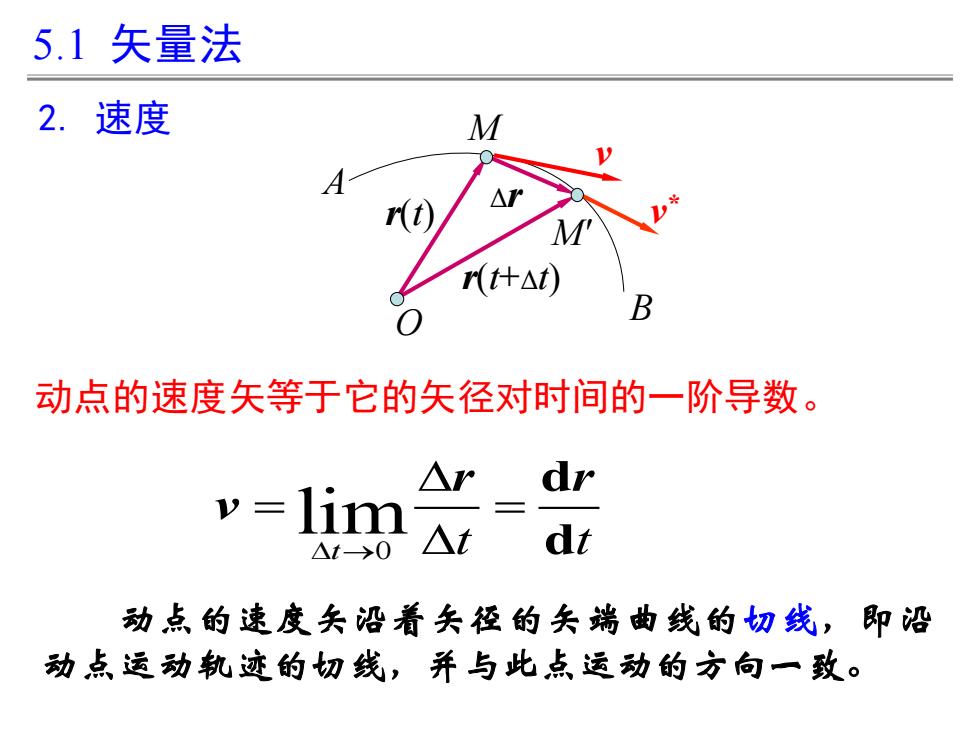
2. 速度 动点的速度矢等于它的矢径对时间的一阶导数。 5.1 矢量法 动点的速度矢沿着矢径的矢端曲线的切线,即沿 动点运动轨迹的切线,并与此点运动的方向一致。 A M B O r(t) r(t+Δt) M' v v Δr * 0 lim →t t t = = d d r r v