
11动量矩定理 日 质点和质点系的动量矩 动量矩定理 日 刷体绕定轴转动的微分云程 口 刷体对轴的转动惯量 质点系相对质心的动量矩定理 刚体平面运动微分方程
11 动量矩定理 • 质点和质点系的动量矩 • 动量矩定理 • 刚体绕定轴转动的微分方程 • 刚体对轴的转动惯量 • 质点系相对质心的动量矩定理 • 刚体平面运动微分方程

引言 。由静力学力象简化理论知:平面任意力系向任一 简化中心简化可得一力和一力偶,此力等于平面力 系的主矢,此力偶等于平面力系对简化中心的主矩。 由则体平面运动理论知:则体的平面运动可以分 解为随同基点的平动和相对基点的转动。 若将简化中心和基点取在质心上,则动量定理(质 心运动定理)描述了刚体随同质心的运动的变化和外 力系主矢的关条。它揭示了物体机械运动规律的一 个侧面。则体相对质心的转动的运动变化与外力系 对质心的主矩的关条将有本章的动量矩定理给出。 它揭示了物体机械运动规律的另一个侧面
引言 • 由静力学力系简化理论知:平面任意力系向任一 简化中心简化可得一力和一力偶,此力等于平面力 系的主矢,此力偶等于平面力系对简化中心的主矩。 • 由刚体平面运动理论知:刚体的平面运动可以分 解为随同基点的平动和相对基点的转动。 • 若将简化中心和基点取在质心上,则动量定理(质 心运动定理)描述了刚体随同质心的运动的变化和外 力系主矢的关系。它揭示了物体机械运动规律的一 个侧面。刚体相对质心的转动的运动变化与外力系 对质心的主矩的关系将有本章的动量矩定理给出。 它揭示了物体机械运动规律的另一个侧面
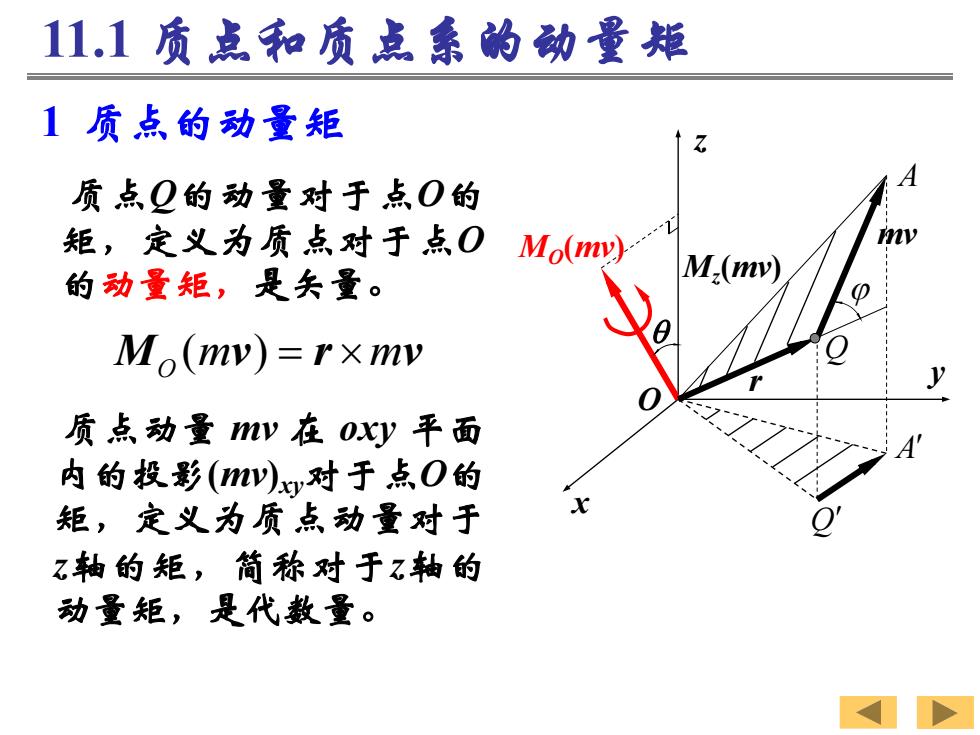
11.1质点和质点系的动量矩 1质点的动量矩 质点Q的动量对于点O的 矩,定义为质点对于点O Mo(m) 的动量矩,是矢量。 M,(w) Mo(mw)=r×mv 质点动量my在OXy平面 内的投影(mw)x对于点O的 矩,定义为质点动量对于 z轴的矩,简称对于z轴的 动量矩,是代数量
1 质点的动量矩 ( ) MO mv r mv 质点Q的动量对于点O的 矩,定义为质点对于点O 的动量矩,是矢量。 11.1 质点和质点系的动量矩 Q A x y z q O A mv Q MO(mv) Mz(mv) r 质点动量 mv 在 oxy 平面 内的投影(mv)xy对于点O的 矩,定义为质点动量对于 z轴的矩,简称对于z轴的 动量矩,是代数量

质点的动量矩 类似于力对点之矩和力对轴之矩的关条,质点 对点O的动量矩矢在乙轴上的投影,等于对乙的动 量矩。 [Mo(mv)l:M.(mv) 在国际单位制中,动量矩的单位是kgS
类似于力对点之矩和力对轴之矩的关系,质点 对点O的动量矩矢在 z 轴上的投影,等于对 z 的动 量矩。 在国际单位制中,动量矩的单位是 kg·m2 /s。 质点的动量矩 [MO(mv)]z=Mz(mv)

质点系的动量矩 2质点系的动量矩 质点条对某点O的动量矩等于各质点对同一点O的 动量矩的失量和。 Lo=∑Momv) 质点象对某轴乙的动量矩等于各质点对同一乙轴的 动量矩的代数和。 Lo=ΣM,(mw) 质点条对某点O的动量矩关在通过该点的z轴上的 投影,等于质点系对该轴的动量矩。 [Lol=La
质点系对某点O的动量矩等于各质点对同一点O的 动量矩的矢量和。 质点系的动量矩 2 质点系的动量矩 LO=ΣMO(mv) 质点系对某轴 z 的动量矩等于各质点对同一 z 轴的 动量矩的代数和。 LO=ΣMz(mv) 质点系对某点O的动量矩矢在通过该点的 z 轴上的 投影,等于质点系对 该轴的动量矩。 [LO]z = Lz