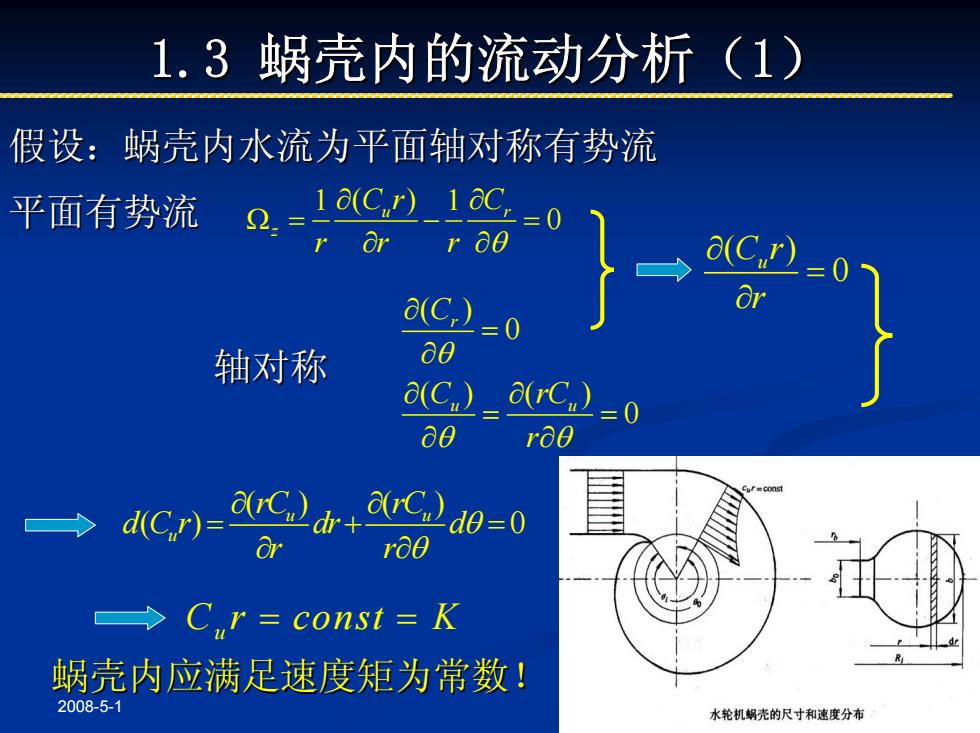
1.3蜗壳内的流动分析(1) 假设:蜗壳内水流为平面轴对称有势流 平面有势流■ .=1aC)_1ag =0 r or r 80 C 2=0 (C) Or =0 轴对称 a0 a(C,)_a(rC,) 0 ae ra0 d(Cr)=9 Cd0=0 Cr=const K R 蜗壳内应满足速度矩为常数! 2008-5-1 水轮机蜗壳的尺寸和速度分布
2008-5-1 6 1.3 蜗壳内的流动分析( 蜗壳内的流动分析(1) 假设:蜗壳内水流为平面轴对称有势流 假设:蜗壳内水流为平面轴对称有势流 1 1 ( ) 0 u r z C r C r r r θ ∂ ∂ Ω = − = ∂ ∂ ( ) 0 ( ) ( ) 0 r u u C C rC r θ θ θ ∂ = ∂ ∂ ∂ = = ∂ ∂ ( ) 0 C ru r ∂ = ∂ ( ) ( ) ( ) 0 u u u rC rC d C r dr d r r θ θ ∂ ∂ = + = ∂ ∂ Cu r = const = K 平面有势流 轴对称 蜗壳内应满足速度矩为常数! 蜗壳内应满足速度矩为常数!
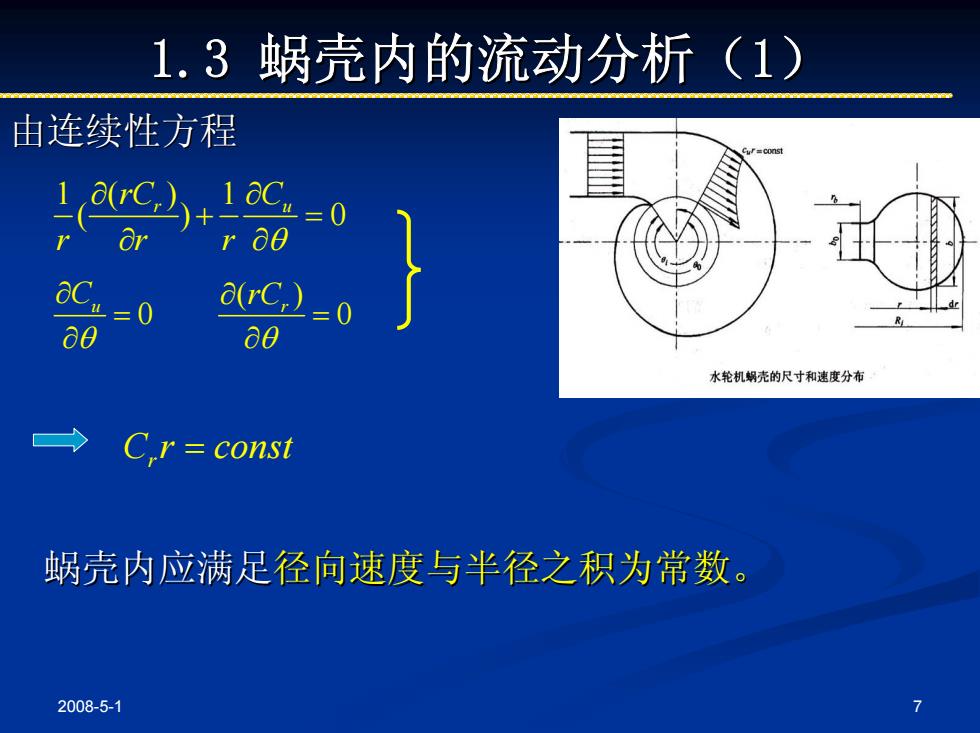
1.3蜗壳内的流动分析(1) 由连续性方程 18C+1aC=0 r or r 00 ac, =0 arC,)」 0 a0 a0 水轮机蜗壳的尺寸和速度分布 C.r const 蜗壳内应满足径向速度与半径之积为常数。 2008-5-1
2008-5-1 7 1.3 蜗壳内的流动分析( 蜗壳内的流动分析(1) 由连续性方程 1 1 ( ) ( ) 0 r Cu rC r r r θ ∂ ∂ + = ∂ ∂ ( ) 0 0 Cu r rC θ θ ∂ ∂ = = ∂ ∂ C rr = const 蜗壳内应满足径向速度与半径之积为常数。 径向速度与半径之积为常数
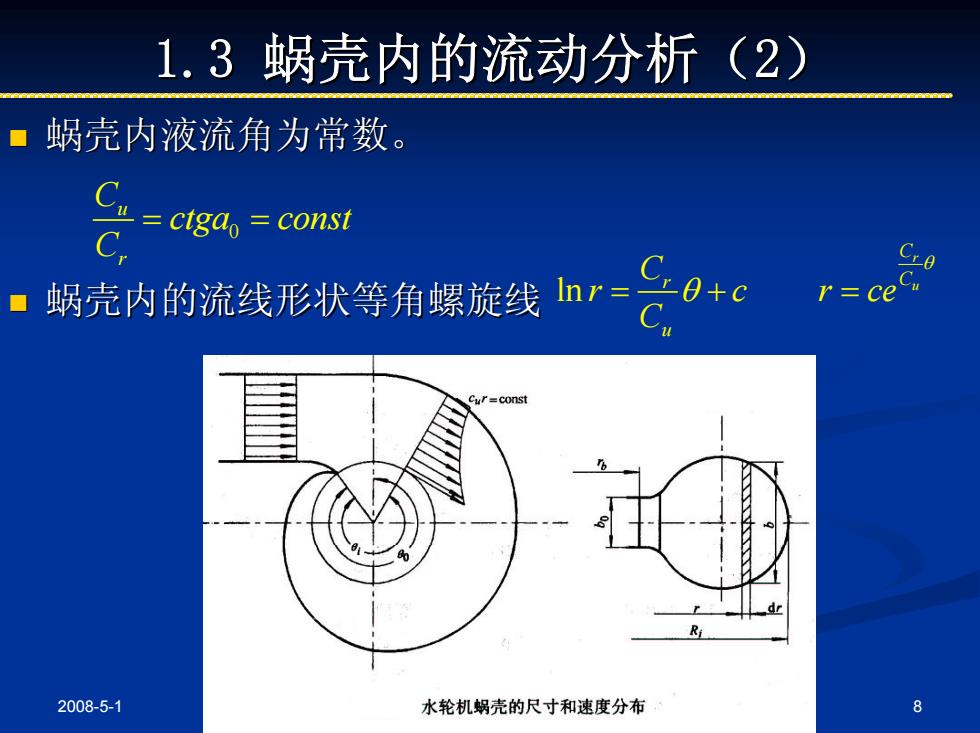
1.3蜗壳内的流动分析(2) ■蜗壳内液流角为常数。 ctga const ■蜗壳内的流线形状等角螺旋线nr= r=ce Cur=const R 2008-5-1 水轮机蜗壳的尺寸和速度分布 8
2008-5-1 8 1.3 蜗壳内的流动分析( 蜗壳内的流动分析(2) 蜗壳内液流角为常数。 蜗壳内液流角为常数。 蜗壳内的流线形状等角螺旋线 蜗壳内的流线形状等角螺旋线 0 u r C ctga const C = = ln r u C r C u C r c r ce C θ = + θ =

1.4水轮机蜗壳的作用原理 ■1)蜗壳形成的环量 蜗壳的主要尺寸 T=2πrC ■2)蜗壳出口流量(单位高度 Q=2πrC ■3)蜗壳内任意断面的流量: 360 或 水轮机蜗壳的尺寸和速度分布 Q,="C.b(r)dr-k[" 4)蜗壳内的速度矩常数 k=Cr 2008-5-1
2008-5-1 9 1.4 水轮机蜗壳的作用原理 水轮机蜗壳的作用原理 1)蜗壳形成的环量 )蜗壳形成的环量 2)蜗壳出口流量(单位高度) 蜗壳出口流量(单位高度) 3)蜗壳内任意断面的流量: 蜗壳内任意断面的流量: 或 4)蜗壳内的速度矩常数 )蜗壳内的速度矩常数 Vu r = const = K 2 u Γ = π rC 2 Q r = π Cr i Q Qi ϕ 360 = 0 0 ( ) ( ) R R i i i u r r b r Q C b r dr k dr r = = ∫ ∫ u k C= r 蜗壳的主要尺寸 蜗壳的主要尺寸
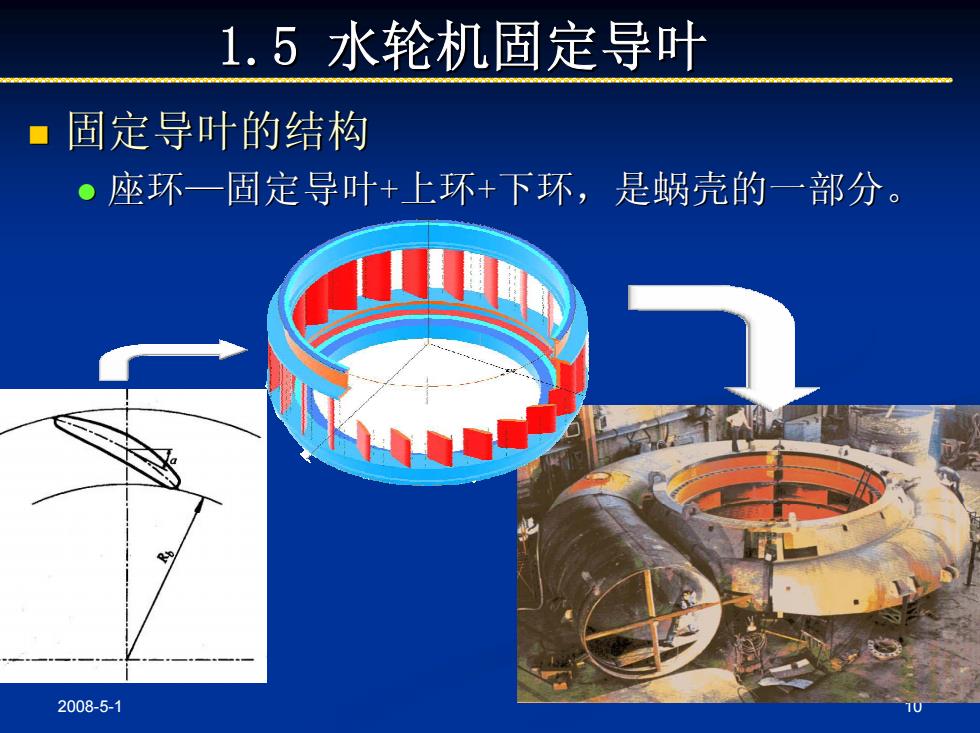
1.5水轮机固定导叶 ■固定导叶的结构 。座环一固定导叶+上环+下环,是蜗壳的一部分。 2008-5-1
2008-5-1 10 1.5 水轮机固定导叶 水轮机固定导叶 固定导叶的结构 固定导叶的结构 z 座环—固定导叶+上环+下环,是蜗壳的一部分。 下环,是蜗壳的一部分