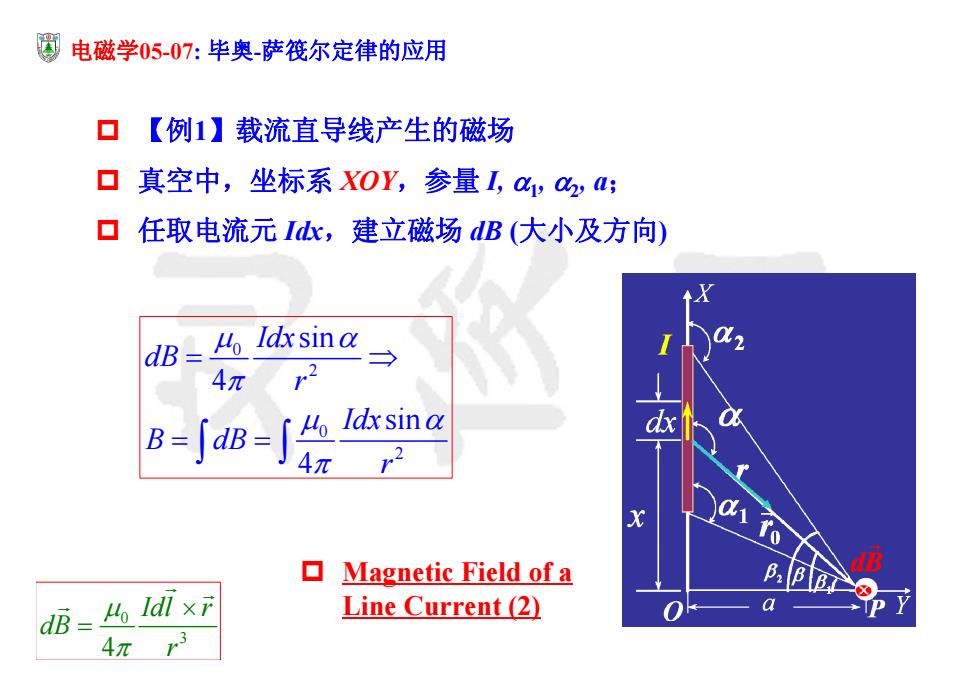
四 电磁学05-07:毕奥-萨筏尔定律的应用 口【例1】载流直导线产生的磁场 口真空中,坐标系XOY,参量I,a,a,: ▣任取电流元Id,建立磁场dB(大小及方向) dB= o Idxsina 4π r2 8jj会n4 dx 01 ▣ Magnetic Field of a B:BB dB=Ho ldlx Line Current (2) a 4π
电磁学05-07: 毕奥-萨筏尔定律的应用 0 2 0 2 sin 4 sin 4 Idx dB r Idx B dB r 【例1】载流直导线产生的磁场 真空中,坐标系 XOY,参量 I, 1, 2, a; 任取电流元 Idx,建立磁场 dB (大小及方向) 0 3 4 Idl r dB r Magnetic Field of a Line Current (2)

电磁学05-07:毕奥萨筏尔定律的应用 ▣统一积分变量: dx dx=acsc'ada x=actg(π-a)=-actga r=a/sina ada sin2a =n/sinada-(csa-cosa) 4πa 4πa B= (cosa-cosa.)(sin B-sin B) 41 Ana 4πa a1=0,4=π→B=46l ▣推广与推论: 2πa a=π/2,42=π→B=4,l 4πa
2 1 2 2 0 0 2 2 0 0 1 2 21 2 0 0 1 2 csc ( ) sin sin sin sin 44s (cos cos ) (sin sin ) 4 4 in sin (cos cos ) 4 4 dx a d x actg actg r a I dx ad B I r a I I d B a a I B a a I 电磁学05-07: 毕奥-萨筏尔定律的应用 统一积分变量: 推广与推论: 0 1 2 0 1 2 0, 2 / 2, 4 I B a I B a
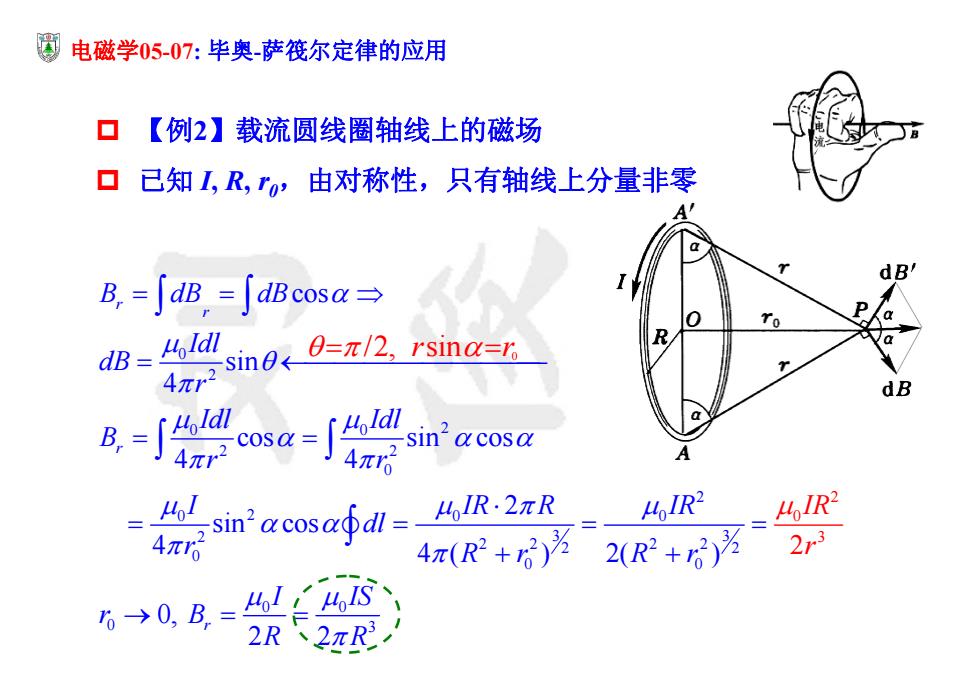
圆电磁学05-07:毕奥-萨筏尔定律的应用 口【例2】载流圆线圈轴线上的磁场 口已知I,R,r,由对称性,只有轴线上分量非零 dB B,=∫dB,=dBcosc→ p 9 dB=Bl sin048=π/2,rsna=r Q 4n dB sin'ccosdl 41R2 =4/R2 4π6 4π(R2+6) 2(R2+7 23 6→0B=卡4因 2R2πR
0 0 2 0 0 2 2 2 0 2 0 00 2 2 3 3 22 2 2 0 3 2 2 2 0 0 0 0 0 0 3 cos sin 4 cos sin cos 4 4 2 sin cos 4 4 ( ) 2( ) 0, 2 2 2 /2, sin r r r r B dB dB Idl dB r Idl Idl B r r I IR R IR d IR l r Rr Rr I S r R r I B R r r 电磁学05-07: 毕奥-萨筏尔定律的应用 【例2】载流圆线圈轴线上的磁场 已知 I, R, r0,由对称性,只有轴线上分量非零
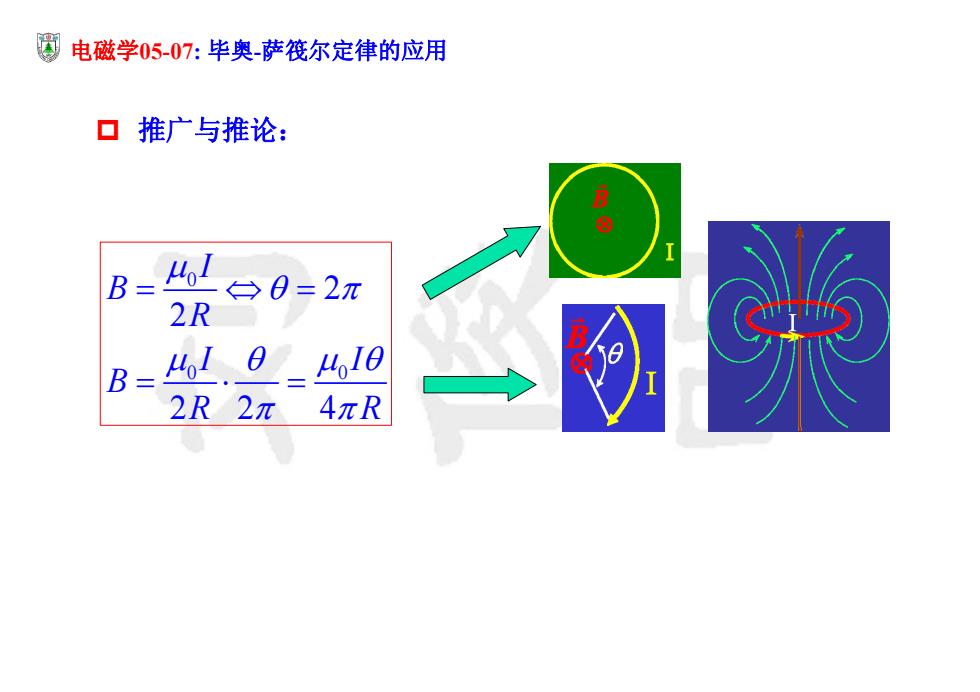
电磁学05-07:毕奥萨筏尔定律的应用 口推广与推论: B B= 461 →0=2元 2R B 410 410 2R2π 4πR
电磁学05-07: 毕奥-萨筏尔定律的应用 推广与推论: 0 0 0 2 2 22 4 I B R I I B R R
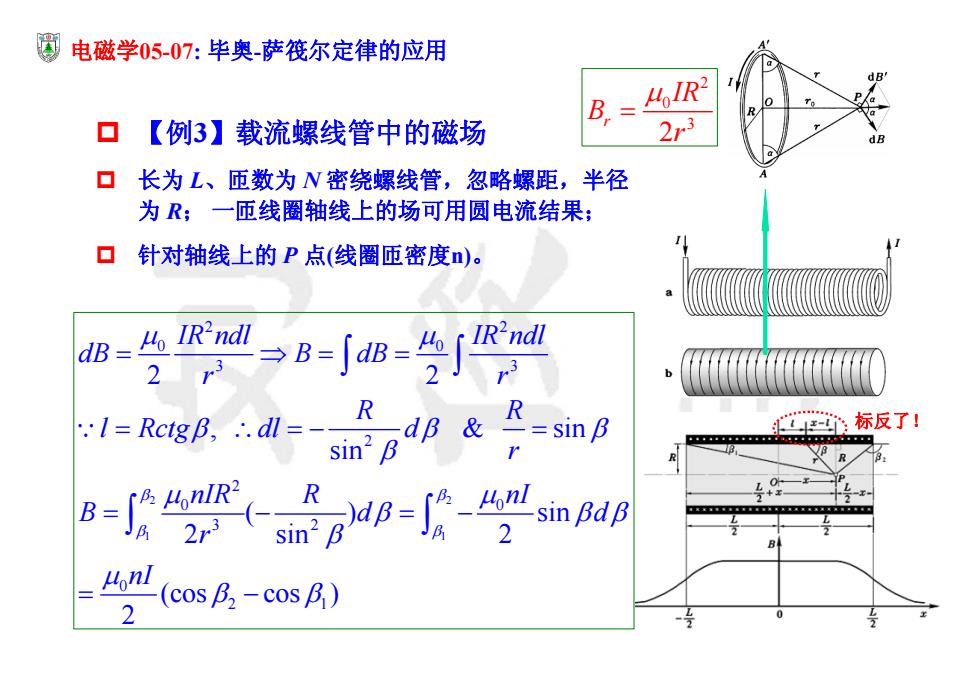
圆电磁学05-07:毕奥萨筏尔定律的应用 B.= oIR2 ▣【例3】载流螺线管中的磁场 2r3 口长为L、匝数为N密绕螺线管,忽略螺距,半径 为R;一匝线圈轴线上的场可用圆电流结果; 口针对轴线上的P点(线圈匝密度)。 dB=凸Rndl 2 I=RetgB,.dl=- R dB R -=sin B :标反了! sin2B s- = R 2-sin BdB Lon! 2 -(cos B2 -cos B)
2 2 1 1 2 2 0 0 3 3 2 2 0 0 3 2 0 2 1 2 2 , & sin sin ( ) sin 2 sin 2 (cos cos ) 2 IR ndl IR ndl dB B dB r r R R l Rctg dl d r nIR nI R B d d r nI 电磁学05-07: 毕奥-萨筏尔定律的应用 【例3】载流螺线管中的磁场 长为 L、匝数为 N 密绕螺线管,忽略螺距,半径 为 R; 一匝线圈轴线上的场可用圆电流结果; 针对轴线上的 P 点(线圈匝密度n)。 标反了! 2 0 3 2 r IR B r