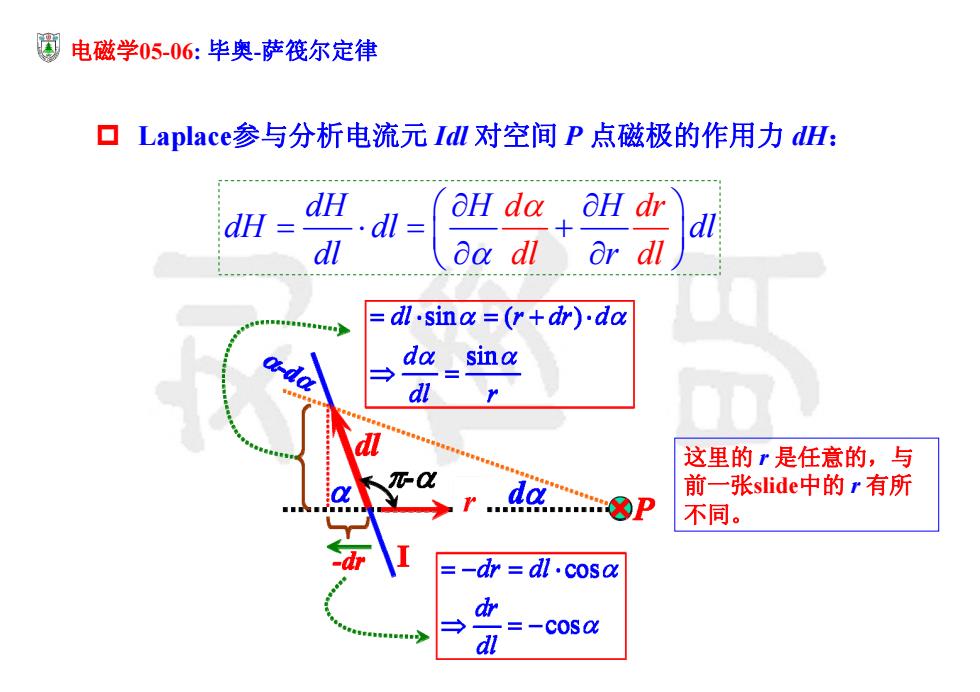
电磁学05-06:毕奥萨筏尔定律 ▣Laplace参与分析电流元Idl对空间P点磁极的作用力dH: dH OH da OH dr dl dl aa dl or dl =dl.sina=(r+dr).da da sina -do dl d 这里的r是任意的,与 元a 前一张slide中的r有所 不同。 -dr =-dr =dl.cosa ar =-cosa d
电磁学05-06: 毕奥-萨筏尔定律 Laplace参与分析电流元 Idl 对空间 P 点磁极的作用力 dH: 这里的 r 是任意的,与 前一张slide中的 r 有所 不同。 d dr dl dH H H dH dl dl dl r dl

圆电磁学05-06:毕奥-萨筏尔定律 ▣Laplace继续卖萌求dH: =dl.sina =(r+dr).da a-da da sina dH d 。 dH .d= H daHdrdl dl da dl ar dl -dr =-dr =dl.cosa H=k-tan dr =-cosa dl aH aH =k Ba r2cos2a/2'O -=-k-2tan da sina dr again ' =-cosa d dl tan(1+cosa)=k Idl Idl .dH k sina
2 2 2 2 ( ) tan , 2 1 , tan tan 2cos / 2 (1 cos ) sin sin , 2 2 cos dH H d H dr dH dl dl dl dl r dl I H k r HI H I Idl I d dr again dl r dl dH k k r r r rr dl k k 电磁学05-06: 毕奥 -萨筏尔定律 Laplace继续卖萌 求dH:
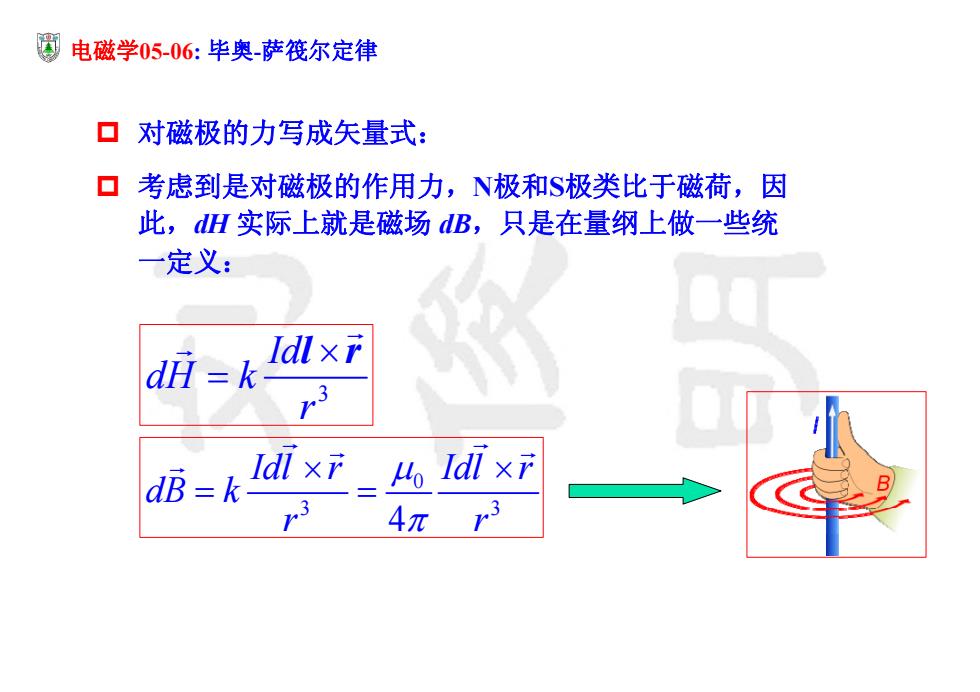
电磁学05-06:毕奥萨筏尔定律 ▣对磁极的力写成矢量式: 口考虑到是对磁极的作用力,N极和S极类比于磁荷,因 此,dH实际上就是磁场dB,只是在量纲上做一些统 一定义: Idl x dH k dB=k Idl×r_Idl×r 3 4πr3
电磁学05-06: 毕奥-萨筏尔定律 对磁极的力写成矢量式: 考虑到是对磁极的作用力,N极和S极类比于磁荷,因 此,dH 实际上就是磁场 dB,只是在量纲上做一些统 一定义: 3 Id dH k r l r 0 3 3 4 Idl r Idl r dB k r r

圆电磁学05-06:毕奥-萨筏尔定律 磁场叠加原理: ▣所有电流元激发的dB的矢量和!→ B=∑B ▣闭合电流在空间所产生的磁场为: B=o Idl×r 4π, ▣闭合电流在磁场中受到的力:一 F=∮dl×B 口若电流散发在广延的导体中: B F=jG×B)dr 4π
电磁学05-06: 毕奥-萨筏尔定律 磁场叠加原理: 所有电流元激发的 dB 的矢量和! 闭合电流在空间所产生的磁场为: 闭合电流在磁场中受到的力: 若电流散发在广延的导体中: B B p i 3 Idl r B r F Idl B 3 j r B d r F ( ) j Bd

电磁学05-07:毕奥萨筏尔定律的应用 ▣计算简单电路的磁场:基本方法 口()选取电流元Idl或选取典型载流导线元,写出其dB; ▣(2)建立坐标系,对dB求矢量和或分量求和,注意磁场的分布; ▣(3)对某些载流导体的组合体,直接应用叠加原理计算
电磁学05-07: 毕奥-萨筏尔定律的应用 计算简单电路的磁场:基本方法 (1) 选取电流元 Idl 或选取典型载流导线元,写出其 dB; (2) 建立坐标系,对 dB 求矢量和或分量求和,注意磁场的分布; (3) 对某些载流导体的组合体,直接应用叠加原理计算