
a (b) 图1,7信号的图形表示:()连续时间信号:(6)离散时间信号 信号则是通过对连续时间信号的采样而得到的,这时该离散时间信号x[】则代表了-一个自 变量是连铵变化的连续时间信号在相继的离散时刻点上的样本值。由于近代数字处理器在速 度计算能力及灵活性等方面的进展,因此被用来实现许多这样的实际系统,其范围涉及从数 字自动驾驶仪到一般的数字音频系统。.这样的系统都要求利用代表连续时间信号经采样过的 离散时间样本序列,这就是飞机的位置、速度和航向,或是音颍系统的语音和音乐。同样,报纸 以及本书中所用的照片实际上也都是由很多细小的点格所组成的,其中每一点就代表着相应 于原照片上该点亮度的采样。无论这些离散时间信号来源是什么,信号x[n]总是在n的整 数值上有定义,因此像所谓一个数字语音信号的第3)个样本,以及对某一家庭的2)个家庭 成员的平均预算等等都是毫无意义的。 本书大部分都采用分别地,但是并行地讨论离散时间信号和连续时间信号,以使我们能在一种 信号类型中所获得的细节有助于对另一种信号类型的理解。到第7章再回到采样问题中来,这样 我们就可以把连续时间信号和离散时间信号的概念结合起来,以披露这两种信号之间的关系。 1.1.2信号能量与功率 从到目前为止所给出的例子可以看到,信号可以表示范围很广的一些现象。在很多(但不 是全部)应用中,所考虑的信号是直接与在某一物理系统中具有功率和能量的一些物理量有关 的。例如,若()和()分别是阻值为R的某-·电阻上的电压和电流,那么其瞬时功率就是 p()=()i(t)=京2() (1.1) 在时间间隔t1≤t≤t2内消耗的总能量就是 p)de d (1.2)

其平均功率为 2f上p0)业=fRd (1.3) 相类似,对于图1.2中的汽车,由于摩擦所耗散的瞬时功率是p(:)=(t),然后就可以按 (1.2)式和(1.3)式来定义在其一段时间内的总能量和平均功率。 利用这些简单的实际例子作为楔子,就可以对任何连续时间信号x(:)或离散时间信号 x[π]采用类似的功率和能量的术语。然而,不久将会看到,往往把信号看作具有复数值更为 方便,这时在t1≤t≤2内的总能量对于一个连缕时间信号x(t)来说就定义为 x()d (1.4) 这里|x记作x(可能为复散)的模。其平均功率将(1.4)式用t2~t1除就可得到。相类似,在 ":≤n≤n2内的离散时间信号x[n]的总能量就是 (1.5) 将其除以2一花1+1就得到在该区间内的平均功率。要牢记的是,这里所用的“功率"和“能 量”与(1.4)式和(1.5)式中的量是否与真正的物理量相联系是无关的①。尽管如此,我们仍发 现采用这些术语在一般意义上是方便的。 再者,在很多系统中关心的是信号在一个无穷区间内(即-<t<+∞或-0<n<+ ∞)的功率和能量,在这些情况下,将总能量定义成按(1,4)式和(1.5)式,将其区间趋于无穷的 极限来考虑,在连续时间情况下就是 E=△,zt)dt=∫广e1x(e)dr (1.6) 而在离散时间情况下就是 B△©芝2=芝1]p (1.7) 注意,对某些信号(1.6)式的积分,或(1.7)式的求和可能不收敛,譬如若x(t)或x[n]在全部 时间内都为某-一非零的常数值就是这样。这样的信号具有无限的能量,而E∞<∞的信号具 有有限的能解 关于在无限区间内的平均功率,可以类似的方式分别定义为 P()Pdt (1.8) 和 PAim2N +1.2 (1.9) 利用这些定义就可以区分三种重要的信号。其中之一是信号具有有限的总能量,即E。<∞。 这种信号的平均功率必须为零,因为在连续时间情况下,由(1.8)式可看出 背著寄凝襄式清型粉电锦整禁隆盆整粱保 5
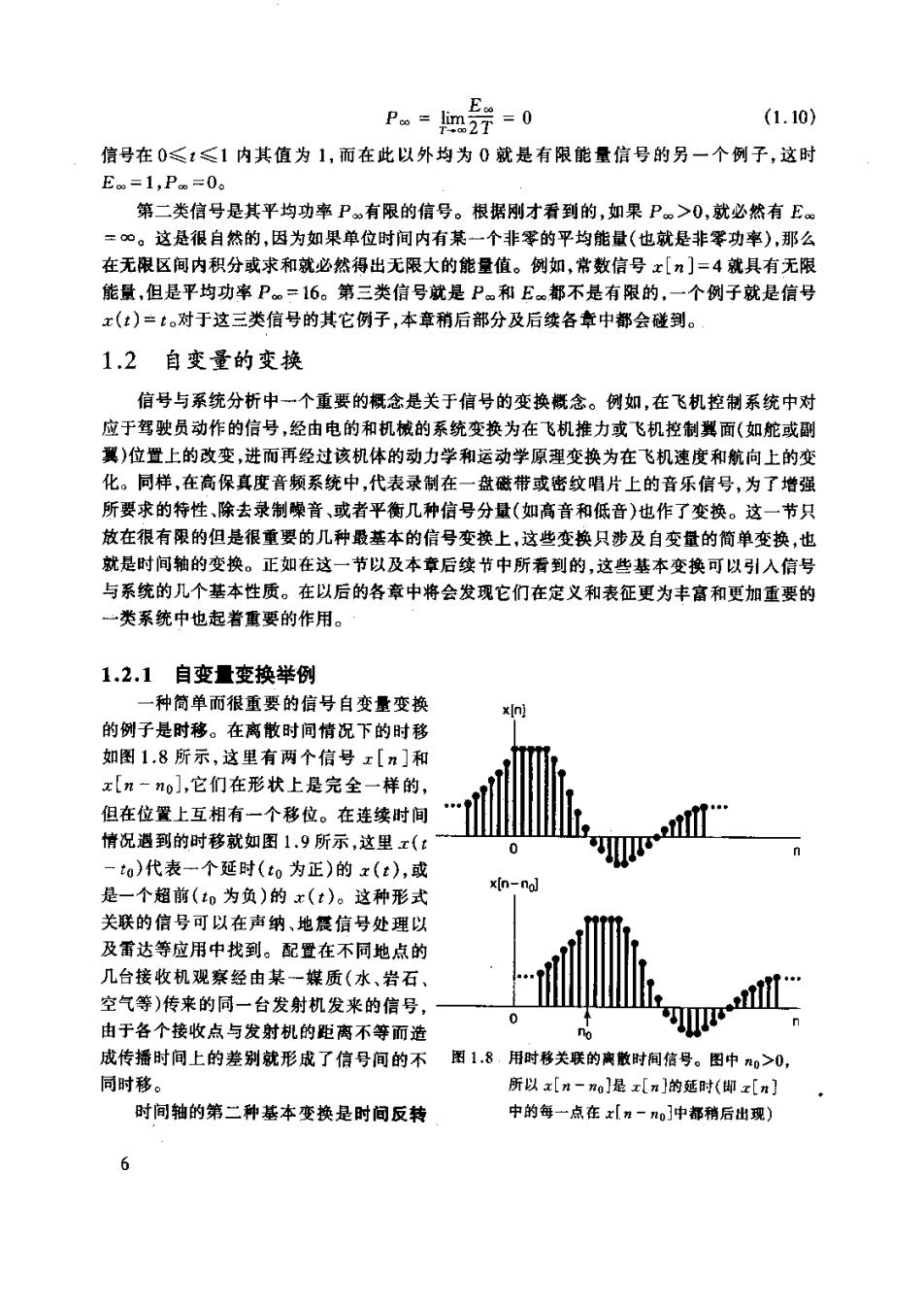
P。=2=0 (1.10) 信号在0≤:≤1内其值为1,而在此以外均为0就是有限能量信号的另一个例子,这时 Eo=1,P.=0o 第二类信号是其平均功率P。有限的信号。根据刚才看到的,如果P。>0,就必然有E 这是很自然的,因为如果单位时间内有某一个非零的平均能量(也就是非功率),那么 在无限区间内积分或求和就必然得出无限大的能量值。例如,常数信号x[n]=4就具有无限 能量,但是平均功率P=16。第三类信号就是P。和E都不是有限的,一个例子就是信号 x(t)=t。对于这三类信号的其它例子,本章稍后部分及后续各章中都会碰到。 1.2自变量的变换 信号与系统分析中一个重要的概念是关于信号的变换概念。例如,在飞机控制系统中对 应于驾驶员动作的信号,经由电的和机械的系统变换为在飞机推力或飞机控制翼面(如舵或副 翼)位置上的改变,进而再经过该机体的动力学和运动学原理变换为在飞机速度和航向上的变 化。同样,在高保真度音频系统中,代表录制在一盘磁带或密纹唱片上的音乐信号,为了增强 所要求的特性、除去录制噪音、或者平衡几种信号分量(如高音和低音)也作了变换。这一节只 放在很有限的但是很重要的几种最基本的信号变换上,这些变换只涉及自变量的简单变换,也 就是时间轴的变换。正如在这一节以及本章后续节中所看到的,这些基本变换可以引入信号 与系统的儿个基本性质。在以后的各章中将会发现它们在定义和表征更为丰富和更加重要的 ~类系统中也起者重要的作用。 1.2.1自变量变换举例 一种简单而很重要的信号自变量变换 的例子是时移。在离散时间情况下的时移 如图1.8所示,这里有两个信号x[n]和 x[n一o],它们在形状上是完全一样的, 但在位置上互相有一个移位。在连续时间 情况遇到的时移就如图1.9所示,这里x(: 一to)代表一个延时(to为正)的x(t),或 是一个超前(o为负)的x(t)。这种形式 关联的信号可以在声纳、地震信号处理以 及雷达等应用中找到。配置在不同地点的 几台接收机观察经由某一煤质(水、岩石 空气等)传来的同一台发射机发来的信号 由于各个接收点与发射机的距离不等而造 成传播时间上的差别就形成了信号间的不 图1,8,用时移关联的离散时间信号。图中0>0 同时 所以x[n-]是x[n]的延时(即z[m] 时间轴的第二种基本变换是时问反转 中的每一点在x「力一。中都稍后出理 6

(time reversal)。例如在图1.10中,x[-#]就是将x[n]以?=0为轴反转而得到的。同样图 1.11中,x(-t)也是从信号x(:)以t=0为轴反转而得的。这样,如果x(:)是代表一盘录制 的声音磁带的话,那么x(一)就代表同样一盘磁带倒过来放(即从末尾向前倒放)的结果。第 三种基本变换是时间尺度变换(time scaling)。在图1.l2中示出了x(t),x(2t)和x(t2)三 个信号,这三个信号是与自变量的线性尺度变换联系者的。倘若我们再一次把x(:)想象为 盘录音磁带的话,那么x(2:)将是这盘磁带以两倍的速度放音的结果,而x(t几)则代表原磁 带将放音速度降低一半。 x[n] 图1.9用时移关联的连续时间信号。图 中o<0,所以x(:-0)就是 b 超前的x(:)(即在x(:)中的每 点在x(1-0)中都提前出现) 图1.10(a)南散时间信号x[元]: (《b)x[n]以#=0为轴反转后的x[一n】 2 图1.11()连续时间信号x(:: 图112用时间尺度变换关联的选续时间信号 (b)x()以t=0为轴反转后的x(-t)

常常关注的是对某一个已知的信号x(t),通过自变量变换以求得一个形式如x(吐+3) 的信号,这里α和是一个给定的数。这样一种自变量变换所得到的信号除了有一个线性的 扩展(若|a1<1)或压缩(1a|>1),时间上的反转(a<0)及移位(≠0)外,仍旧保持有x(t)的 形状。现用下面的一组例子给予说明。 例【.1已知信号x(t)如图1.13(a)所示,x(t+1)就是x(t)沿:轴左移一个单位如图1.13(6)所示。其体 地说,x(t)在=t0慰得的值.在x《:+1》中发生在=一1.例如x《:)在=1的值在x《+1》中 是在1=1-1=0处得到。同样,因为x()在t<0为,所以x(t+1)在t<-1为零:相类似,因 为x(t)在:>2为零,所以x(t+1)在>1为零。 现在考虑信号x(-t+1),这可以在x(t+1)中以一1代替:来得到,这就是说,x(-t+1)就是(t +1)的时闻反转。因此x(-t+1)河以在图上以:=0为轴将x(t41)反转而得到,如图1.13()所示 ,x e 图1.3(a)用于例1.1~1.3的连续时间号x(:),图示说男自变变换: (b)时移信号x(t+1) (c)用时移和反转得到的x(-t+1): (d)时间尺度变换信号x(号):(e由时移和尺度变换得到的x(:+1)