《物理化学》课程教学资源（A）Ⅱ 物理化学辅导与习题详解（共十四章）

·34:物理化学辅导与习题详解30.00×(800-373)+X10.7X10-3×(80023732）J.mol-1=15.49kJ·mol-12反应在800K时的摩尔反应恰变A,H(800 K) = AH, +AHz + AH:+ AH, +AH,=- 248.08 kJ .mol-133，某高压容器中含有未知气体，可能是氧气或氩气。今在298K时，取出一些样品，丛5dm绝热可逆膨胀到6dm，温度降低了21K，试判断容器中是何气体。设振动的贡献可忽略不计。解设气体为理想气体。绝热可逆过程方程式TV'-1 =T-V-1In(T,/T)_ln[(298-21)/298]+1=1.40y=+1=In(V,/V2)In(5/6)Cv.m+RCpm元又因为Y-Cv,mCv.mCv,m+R5RR=1.40,所以Cv.mCv,m2根据能量均分原理，单原子分子只有3个平动自由度，其热容为号R；双原子分子在不考虑振动自5由度时，有3个平动自由度和2个转动自由度，其热容为-号R。所以该未知气体是氮气。34.将H,O看做是刚体非线性分子，用经典理论来估计其气体的Cm（HzO，g）值。（1）在温度不太高时，忽略振动自由度项的贡献；（2）在温度很高时，将所有的振动贡献都考虑进去。解（1）H,0是三原子非线性分子，在常温时（不考虑振动自由度），有3个平动自由度和3个一T，所以转动自由度，每个自由度对能量的贡献为UmkT×6×L=3RTauCy.m=3RCp.m=Cv,m+R=4R=33.26Jmol-1.K-1（2）在高温时，还要考虑（3×3一6）个振动自由度，每个振动自由度有2个平方项，对能量的贡献为kT，所以U.=kT×6+T×3×L=6RTa= 6RCv,mCp.m=Cv.m+R=7R=58.20J.mol-1.K-135.在环境温度为298K、压力为100kPa的条件下，用乙炔与压缩空气混合，燃烧后用来切割金属，试粗略计算这种火焰可能达到的最高温度，设空气中氧的含量为20%。已知298K时的热力学数据如下：物质Cem/J.mol-1.K-1)A,He /(kJ : mol-1)CO2(g)393.5137.1H,O(g)-241.8233.58C,H2(g)226.743.930N(g)29.12

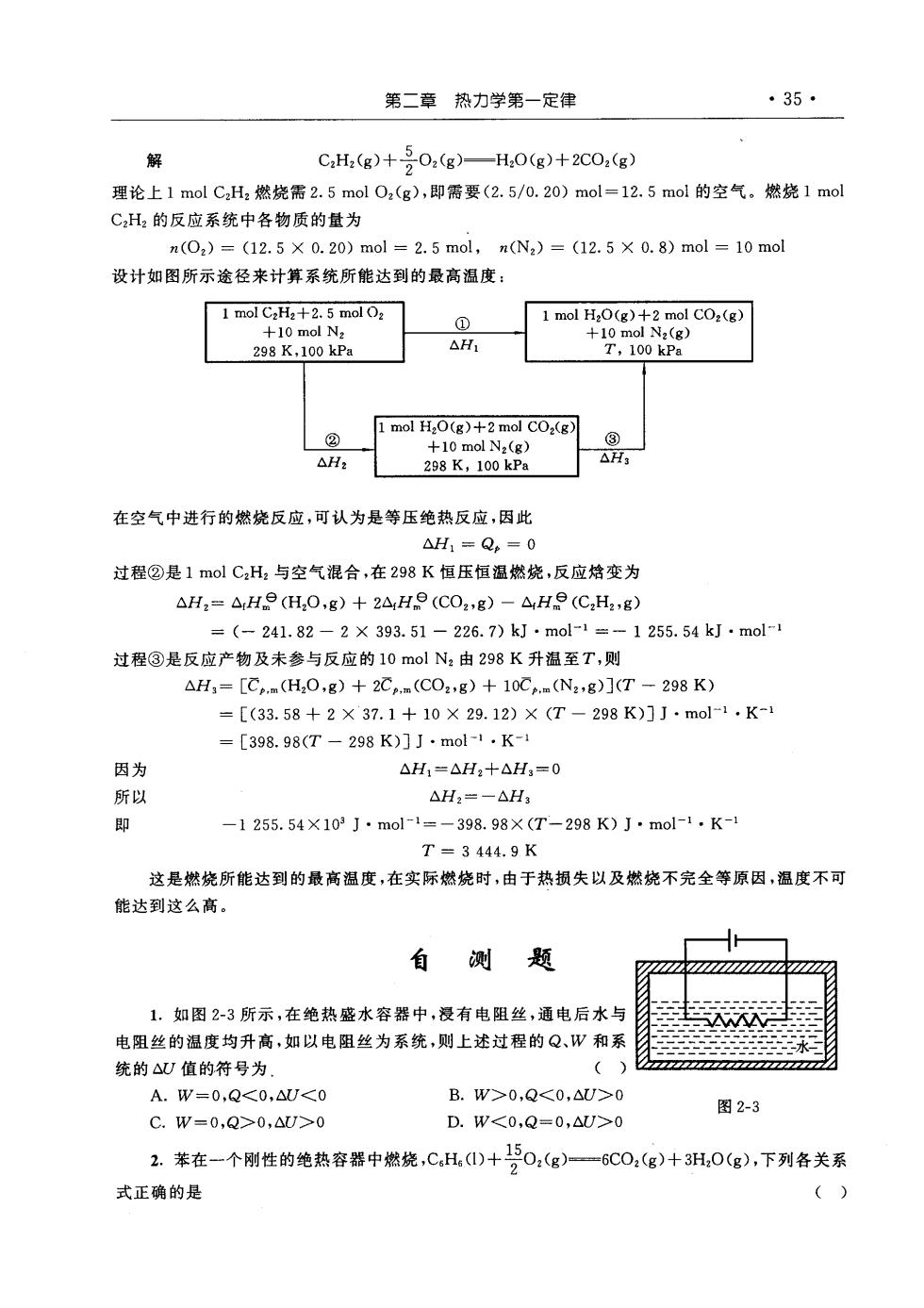
:35·第二章热力学第一定律502(g)C,H2(g)+-解H20(g)+2CO2(g)理论上1molC,Hz燃烧需2.5molOz(g），即需要（2.5/0.20）mol=12.5mol的空气。燃烧1molC,H2的反应系统中各物质的量为n(0z)=(12.5X 0.20)mol=2.5mol,n(N2)=(12.5×0.8)mol=10mol设计如图所示途径来计算系统所能达到的最高温度：1mol C,H2+2.5mol 021 mol H,O(g) +2 mol CO2(g)@+10 mol N2+10 mol Nz(g)AH,T,100kPa298K,100kPa1molH,O(g)+2molCO,(g)?②+10mol Nz(g)AH:AH2298K,100kPa在空气中进行的燃烧反应，可认为是等压绝热反应，因此AH1= Q,= 0过程②是1molCzHz与空气混合，在298K恒压恒温燃烧，反应恰变为AH,= AHe(H,O,g) +2,H(CO2,g) -AH(C,H2,g)= (—241.82—2X 393.51-226.7) kJ ·mol-1=1255.54kJ.mol-1过程③是反应产物及未参与反应的10molN，由298K升温至T，则AH.=[Cp.m(H,O,g) +2Cpm(CO2g) +10Cm(N2.g)(T-298K)=[(33.58+2×37.1+10×29.12)×(T298K)IJ.mol-1.K-1= [398.98(T- 298K)JJ·mol-1.K-1因为AH=AH2+4H:0所以AH2-—AH3即-1255.54×103J.mol1=-398.98X(T-298K)J.mol-1.K-1T = 3 444. 9 K这是燃烧所能达到的最高温度，在实际燃烧时，由于热损失以及燃烧不完全等原因，温度不可能达到这么高。自藍测题x1.如图2-3所示，在绝热盛水容器中，浸有电阻丝，通电后水与电阻丝的温度均升高，如以电阻丝为系统，则上述过程的Q、W和系统的AU值的符号为，A. W-0,Q<0,AU<0B. W>0,Q<0,AU>0图2-3D.W<0,Q=0,AU>0C. W=0,Q>0,AU>02. 苯在一个刚性的绝热容器中燃烧,C.H。(1)+150(g)—6CO:(g)+ 3H,0(g),下列各关系2()式正确的是

:36:物理化学辅导与习题详解A. AU=0,AH<0,Q-0B.△U-0,AH>0,W-0D.Q<0,W0,AU<0C.△U=0,4H=0,Q=0()3.VanderWaals气体绝热向真空膨胀后，气体的温度A.升高B.降低C.不变D.不确定O,(g)—ZnO(s),AH=351. 5 kJ ·mol-,Hg(s)+02(g)4.已知：Zn（s）+一22HgO(s)，△,H=90.8 kJ ·mol-l。因此Zn(s)+HgO(s)=ZnO(s)+Hg(s)的△,H是（)A.442.2kJ·mol-1B.260.7kJ·mol-1C. -62. 3 kJ ·mol-1D. -442.2 kJ ·mol-15.1mol单原子理想气体，从273K、202.65kPa，经pT=常数的可逆途径压缩到405.3kPa的终态，该过程的U是()A.1702 JB. -406. 8 JC. 406.8 JD. -1 702 J6.理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到达相同的压力，则其终态的()温度、体积和系统的焰变必定是AT（可逆）>T（不可逆），V（可逆）>V(不可逆），AH（可逆）>AH（不可逆）B.T（可逆）<T（不可逆），V（可逆）<V（不可逆），AH（可逆）<AH（不可逆）C.T（可逆）<T（不可逆），V（可逆）>V（不可逆），AH（可逆）<AH（不可逆）D.T（可逆）<T（不可逆），V（可逆）<V（不可逆），AH（可逆）>AH（不可逆）7.在一个体积恒定的绝热箱中有一绝热隔板，其两侧放有n、T、p皆不相同的N(g),Nz(g）视为理想气体。今抽去隔板达到平衡，以N2(g）作为系统，此过程的()A.W=0,AU=0,4H=0B. W>0,4U>0,4H>0C.W<0.AU<0.AH<0D. W-0,AU-0,AH>08.△H=Q，适用于下列哪个过程？()A.理想气体从1×10'Pa反抗恒定的压力1×105Pa膨胀到1×105PaB.0C、101325Pa下冰融化成水C.101325Pa下电解CuSO,水溶液D.气体从298K、101325Pa可逆变化到373K、10132.5Pa9.某气体在恒压升温和恒容升温过程中（不做非体积功)所吸收的热量相同，比较恒压过程体系升高的温度（dT），与恒容过程体系升高的温度（dT)的大小()A. (dT),>(dT)vB. (dT),=(dT)vC. (dT),<(dT)vD. (dT)≥(dT)v10.一定量气体从298K、p恒温压缩时，系统的恰增加，则该系统从298K、p节流膨胀到邻近某一状态时，系统的温度必将()A.升高B.降低C.不变D.不能确定11.1mol单原子理想气体，始态为p1=202650Pa，T=273K，沿可逆途径p/V=K（K是常数）至终态，压力增加一倍。（1）计算VI、V2、T2、Q、W、AU、AH；（2）计算该气体沿此途径的热容C。12.容器中放有100gN2，温度与压力分别为25℃和3039.75kPa，若该气体反抗1013.25kPa压力等外压绝热膨胀，试计算系统的最终温度T和过程的△U、△H。假定N2是理想气体，且Cv,m=20.71J.mol-1.K-1。13.一个绝热容器原处于真空状态，用针在容器上刺一微小孔隙，使298K、101325Pa的空气

·37第二章热力学第一定律缓缓进入，直到压力达平衡，求此时容器内的空气温度。（空气可视为双原子理想气体。）14.p及25C时，将1mol CaO和1mol CaCO，分别溶于1molL-的HCl中，放热为193.3kJ和15.02kJ。请计算1kg25℃的CaCO，变为885C的CaO和CO，需多少热量。已知CaO和COz的平均比热容分别是0.895J·g-1K-1和1.013J·g-1·K-1。15.298.15K时，5.27g的甲醇在弹式量热计中燃烧，放热119.50kJ。已知AHe（H,O,1)一285.84kJ·mol-1,A/H（CO2g）=393.51kJ·mol-。（1）计算甲醇的燃烧AHe；(2）用H,O(I)和CO2(g）的标准摩尔生成焰计算CH:OH(1)的AH；（3）如果甲醇的蒸发恰为35.27kJ·mol-1,计算CH,OH(g)的△,H。自测题参考答案1. B.2.B。苯在刚性绝热容器中燃烧，压力增加，△H=P2V一PiV>0。3.B。绝热自由膨胀，Q=0，W0，AU=0。范德华气体分子间存在作用力，气体体积增大，分子间距离增加，分子间势能增加，但AU=0，所以分子动能要降低，温度降低。4. B。3R/ pTi%R×273K×5. D。Tz=p)T/p2,AU=nCv,m(T,-T)=1 molX-=1 molXP22202.65-1 702 J。405.36.B。绝热可逆过程比绝热不可逆过程做的功要多，到达同一压力时，绝热可逆过程终态的温度要低于绝热不可逆过程终态的温度，绝热可逆过程终态的体积也小于绝热不可逆过程终态的体积。AH=C,AT，AT（可逆）<AT（不可逆），所以AH（可逆）<AH（不可逆）。7.A。W=0，绝热系统AUW+Q=0,AH=AU+ApV)=n左RAT+n右R△T右，因为AU=n左Cv.m△T左十n右Cvm△T右0，n左△T左n右△T右，所以AH=0。8. B。9.C。恒压过程有体积功存在。H10. A。该气体的μ=<0,又=，所以节流膨胀时温度升高。nRT:.(1X8.3145X273)11. (1) V,m2=0.0112m3202.650pi因为p/V=KViP2-(0.0112X2X202650)m=0. 0224m2所以V,=p1202650T,=pV(2X202 650X0. 0224) K=1 091. 9 KnR1X8.31453×8.3145×(1091.9-273)J=10.21kJAU=nCv,m(T2--T1)2.[1×号×8.314 5×(1 091.9-273)] J=17. 02 kJAH=nCpm(T2-T,)=2K(Vi-Vi)=--"KVdV-W-(p2V2-piV1)=-3. 40 kJedt2

·38:物理化学辅导与习题详解Q=AU--W=13.61 kJ（2）热力学第一定律d=wdU=nCv,mdT, W=-pdV对理想气体所以Q=nCy.mdT+pdVQdVC=由热容定义得=nCv.m+p(aT)dT将p/V=K代入pV=nRT，得KV?=nRTnRdvT)2VKnR= nCvm + nRK=16.63J.K-1所以= 1 mol XC = nCvm + P2VK212.理想气体绝热膨胀W=AU=nCv,m（T2-T）(nRT,_nRT)Tip2恒外压膨胀W=- 2(V,-V.)-p1P2p,所以Tip2nCy.m(Tz - T) =-nRPi20. 71 × (T, 298. 15 K) =- 8. 314 5 × (T 298. 15 KX1 013.25)3039.75系统最终温度T,=241.21K1002×20.71×（241.21-298.15）AU=nCVm(T2-T)=J=—4212JL28AH=nCp.m(T2-T.)=n(Cv.m+R)(T2-T.)100×(20.71+8.3145)×(241.21—298.15)5902J2813.设进入真空绝热容器的空气的物质的量为n，以空气为系统，则过程的始、终态如下图所示：p1=101325Pa101325pmoTi=298KT2VV,nVi,n当空气进入箱内时，功可分两部分来考虑：原在箱外占有体积为V，的空气全部进人箱内，箱外的体积为0，功为W=一p(0-Vi）=pVi；箱内为真空，进人箱内时，W=0。所以总的功W=pV.+0=pV,绝热箱Q=0所以AU=W=pV,=nRTi又△U=Cv(T2-T1)所以Cr(T,-T)=nRTI(Cv + nR)T = CT2C,T1 = CvT27R/2TX298K=417.2K5R/2