《物理化学》课程教学资源（A）Ⅱ 物理化学辅导与习题详解（共十四章）

4物理化学辅导与习题详解Oz(g）、Nz(g）在潮湿空气中的分压力p(O2)=p(空气)r(O2)=88.995kPa×0.21=18.689kPap(N2)=p(空气）α（N2)=88.995kPa×0.79=70.306kPa5.3.45gHz(g）放在10dm2的密闭容器中，从273K加热到373K，需提供多少能量?Hz（g）的根均方速率是原来的多少倍？已知Hz（g）的摩尔等容热容Cvm=2.5R。3.45X2.5×8.3145×(373—273)J=3.56kJ解 E=nCvm(T,-T)=L2.0163RT根均方速率M373Ku(373 K)所以=1.17u(273K)273K373K时H2（g）的根均方速率是273K时的1.17倍。6.计算293K和373K时，H2(g)的平均速率、根均方速率和最概然速率。解293K时8RT8×8.3145×293平均速率V3.14×2.016X10-,m*s-1=1.75×10m.s-1Va元M3RT3×8.3145×293m.s-1=1.90×103m.s-1根均方速率M2.016×10-32RT2X8.3145×293最概然速率m.s-1=1.55×103m.s-Um=M2.016X10-3同理可得373K时U,=1.98×103m?s-1,u=2.15×103m.s-l,Um=1.75×10°m.s-17.计算分子动能大于10kJ的分子在总分子中所占的比例。Ne,解假定分子只在一个平面上运动，分子动能大于E，的分子在总分子中所占的比例为一Ne-假定温度为298K，则动能大于10kJ的分子在总分子中所占的比例为N1o kj-10 X 1030N1.38×10-23X298298K时，没有动能大于10kJ的分子。8.在一个容器中，假设开始时每一个分子的能量都是2.0×10-21J，由于相互碰撞，最后其能量分布服从Maxwell分布。试计算：（1）气体的温度；（2）能量为1.98×10-21J~2.02×10-21J之间的分子在总分子中所占的分数（由于这个区间的间距很小，故用Maxwell公式的微分式）。解（1）分子运动论认为分子的碰撞是完全弹性的，碰撞前后总动量不损失，在外界条件稳定的情况下，气体的力和T都不随时间而改变，所以气体的终止温度与起始温度是一样的。3RTEt.m- Le-12Le2( 6.022X1023X2.0X10-21T-K=96.57K3R38.314 5dNeE)dE21(2)E/2expN(T6T元将π=3.14,k=1.38×10-23J·K-1T=96.57K,E=2.0X10-21J,dE=(2.02-1.98)×10-21J代人上式计算，得

.5.第一章，气体dNE=9.25×10-3N9.根据速率分布公式，计算分子速率在最概然速率以及大于最概然速率1.1倍（即dvm一0.1Vm）的分子在总分子中所占的分数（由于这个区间的间距很小，可用微分式）。解速率在u-u十du间的分子占总分子数的比例为dN,m4mwwexpdzN2kT2kT元2kTdum=0.1um，代人上式得最概然速率VdN,11.52kTm(2kT/m)4m2kT0.4e-1X0.=0.083-expN2kT2kTmmy元元10.在293K和100kPa时，Nz（g）分子的有效直径约为0.3nm，试求：（1）Nz（g）分子的平均自由程；（2）每个分子与其他分子的碰撞频率；（3）在1.0m的体积内，分子的互碰频率。11=解（1）平均自由程2#nd?单位体积分子数L-Lp-6.022×1023×100×103-3=2.472X102m-3n=V."RTm8.3145X29317-=101.2nm:L2 ×3.14X2.472×1025×(0.3×10-92元nd2（2）一个分子与其他分子的碰撞频率/8RT2'= 2 nd'nu.= /2 nd'n /T8×8.3145×293=23.14×(0.3X10-9)2×2.472X10253.14X28.014X10=4.65×10s-（3）同种分子的互碰频率RTz=2n'rd /RM8.3145×2932X(2.472X1025)2×3. 14×(0.3×10-9)2X3.14×28.014×10-3=5.75×103s-111.一个容积为0.5m的钢瓶内，放有16kg温度为500K的CH（g），试计算容器内的压力。(1）用理想气体状态方程；（2）由vanderWaals方程。已知CH（g）的常数a=0.228Pa·m°mol-2，b=0.427X10-^mmol-1,M(CH,)=16.0g·mol-l。16×103gm解CH的物质的量n==1 000 molM16.0g.mol-（1）用理想气体状态方程计算nRT1000X8.3145X500)Pa = 8. 31 × 10° Pap=V0. 5（2）由vanderWaals方程计算

.6.物理化学辅导与习题详解nRTna10002×0.228)1000X8.3145X500Pa=8.18×10°Pap=V-nb-Vz（0.5-1000×0.427×10-40.5212.已知CO，（g）的临界温度、临界压力和临界摩尔体积分别为T。=304.3K，P。=73.8×105Pa，V.s=0.0957dm2.mol-1。（1）试计算CO,(g）的vanderWaals常数a，b的值(2）313K时，在容积为0.005m的容器内含有0.1kgCOz（g），用vanderWaals方程计算气体的压力；（3）在与（2)相同的条件下，用理想气体状态方程计算气体的压力。27RT8.31452×304.3227、解Pa·m?.mol-2=0.3659Pa·mmol-2(1) a64pe6473.8X105RT.（8.3145×304.3)m2.mol-1=0.429×10-*m3.mol-16:8pe8×73.8×1050.005m2(2) Vm==2.20×10-3m3.mol-1100g/(44g·mol-1)RT8.3145×3130.36594Pa=1. 13X106 Pap=V.-6-V2(2.20×10-3)2L2.20×10-3-0.429×10-4RT（8.3145×313）(3)p:Pa=1.18×106PaV.m2.20×10-3av13.热膨胀系数的定义为α一，试列式表示热膨胀系数与温度、体积的关系。（1）设气VlaT体为理想气体；（2）设气体为vanderWaals气体。解（1）理想气体状态方程为pV=nRT在等压条件下对理想气体状态方程两边微分，得(av)nRarP1nR1/1所以4=TVLaTlVp热胀系数与温度成反比，与体积无关。nRTn’a（2）vanderWaals方程p=V-nb6-V2nRapV-nbLaT)nRT2an?ap nbje +3av(Vap)ava因为=-1abnR(ap/aT)yV-nbRVs(V- nb)所以(ap/a)rnRTRTV3-2an(V-nb)22an2V3-nb)2RV?(V - nb)(av)as（)RTV32an(V-nb)214.NO（g）和CCl（g）的临界温度分别为177K和550K，临界压力分别为64.7×105Pa和45.5X105Pa。试用计算回答：（1）哪一种气体的vanderWaals常数a较小；（2）哪一种气体的vanderWaals常数6较大；（3）哪一种气体的临界体积较大；（4）在300K和10×105Pa的压力下，哪-种气体更接近于理想气体。27R3T2解(1)a=64pe

·7第一章气体278. 314 52 X 1772Pa.m.mol-2= 0.141 2 Pam.mol-2a(NO)6464. 7 X 105278.31452×5502Pa·mmol-2= 1.939 Pa·m5.mol-2a(CCI)=X6445.5×105NO(g）的van der Waals 常数a较小。RT.(2) b=8pe8.3145X1776(NO)=m.mol-1=0.284X10*m2.mol-18X64.7X1058.3145×550m2.mol-1=1.26×10-4m2.mol-1b(CCl,)=8X45.5×105CCl,(g)的vanderWaals常数b较大。（3）因为Vm.=3b，所以CCl,（g）的临界体积较大。(Vm-6)=RT(4)van derWaals方程p12由于NO(g）的a、b值都小于CCl,(g）的，所以NO(g）的vanderWaals方程中的校正项要小于CCl(g）的，因此NO（g）更接近于理想气体15.在273K和100kPa时，有1mol某实际气体符合Virial型状态方程，pV=A+Bp十Cp2已知第二Virial系数B=2×10-m·mol-1，试求该气体在这时所占的体积。解Virial型状态方程可写成pV=RT+Bp+Cp，忽略第三Virial系数，则pV=RT+Bp，所以RT +B(8.314. 5X273 +2×10-5Vm2.mol-1=0.0227m3.mol-1100X103P16.373K时，1.0kgCOz（g）的压力为5.07×10°kPa，试用下述两种方法计算其体积。（1）用理想气体状态方程式；（2）用压缩因子图。nRT（1000/44)×8.3145×373解(1)V=3-0.0139m55.07×10×10：（2）查表得COz（g）的临界温度和临界压力为T。=304.3K,p。=73.8X105Pa上=5.07×10%对比压力元二=0.687Pe-73.8×105T373对比温度-1.226T304.3由对比压力及对比温度在压缩因子图上查得Z=0.9，所以V=ZnRT(1000/44)X8.3145×3730.9 Xm2=0.0125m35.07×103X103p17.在273K时，1molNz（g）的体积为7.03×10-5m2，试用下述几种方法计算其压力，并比较所得数值的大小。（1）用理想气体状态方程式；（2）用vanderWaals气体状态方程式；（3）用压缩因子图（实测值为4.05×101kPa）。RT(8.3145×273)解(1)p=Pa=3.23X107PaV..7.03X10-5(2)N2(g)的van der Waals 常数a=0.136 8 Pa·m:mol-2,b=0.386X10-m2·mol-1。RT8.3145X2730.1368aPa= 4. 39 × 10° PabVm-b-Va7.03×10-5-0.386×10-4(7.03X 10-5)2

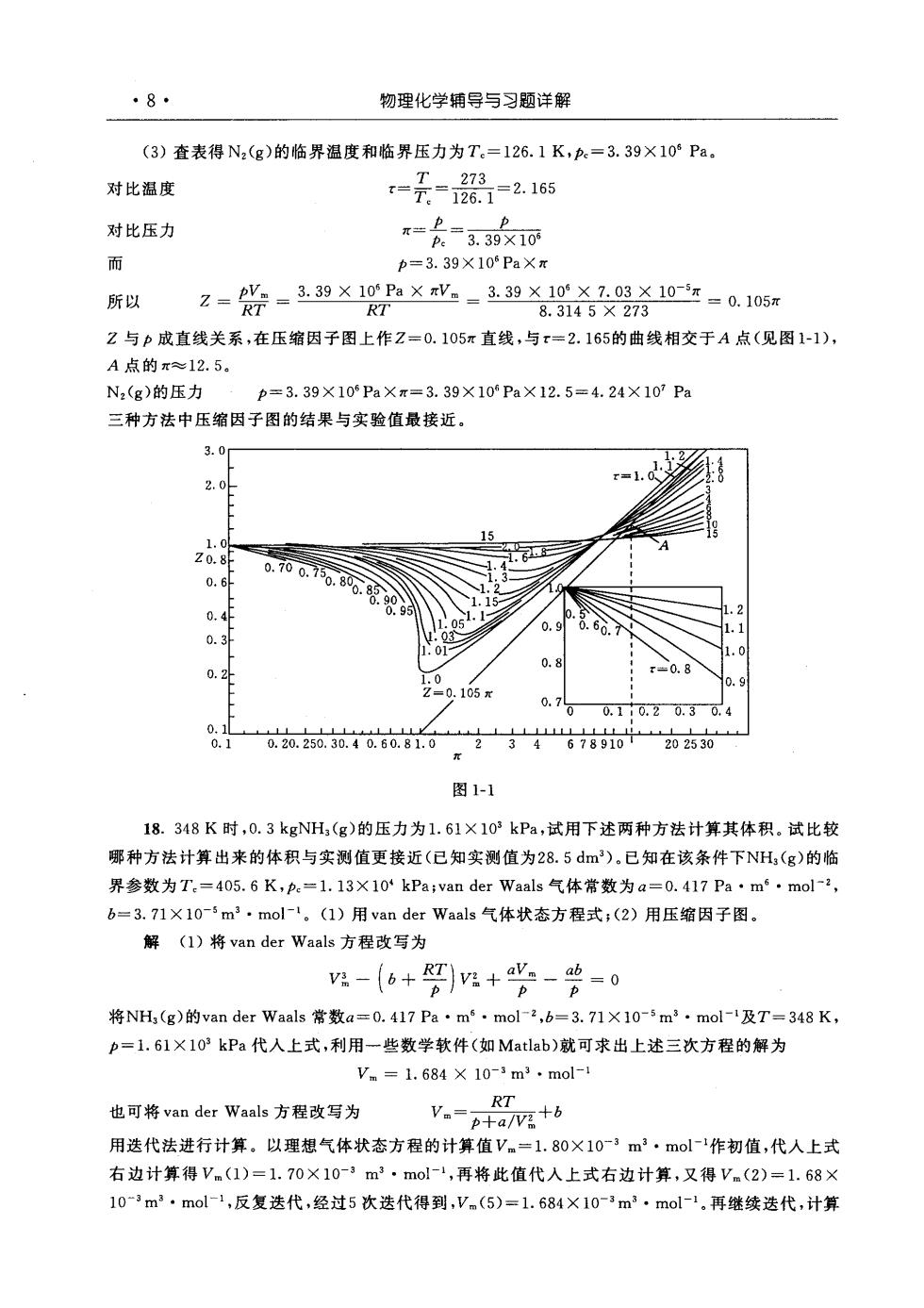
.8.物理化学辅导与习题详解（3）查表得N2(g)的临界温度和临界压力为T。=126.1K，pe=3.39×10°Pa。T273对比温度=2.165T126.1pp对比压力元3.39×105p而p=3.39×10°Pa×元3. 39×10° Pa×Vm3.39×10°×7:03X10元=0. 105元pVmZ=所以RTRT8.3145X273Z与p成直线关系，在压缩因子图上作Z=0.105元直线，与t=2.165的曲线相交于A点（见图1-1），A点的元～12.5。N2(g)的压力p=3.39X10°PaX元=3.39×10°Pa×12.5=4.24X107Pa三种方法中压缩因子图的结果与实验值最接近。3. 02.0151.0Z0.8F0.700.750.650.80g0.850.90.20.90. 4F1. 10.30.80.80.210.90.105x0.70.10.20.30.40.10.10.20.250.30.40.60.81.023467891020 2530r图 1-118.348K时，0.3kgNHs（g）的压力为1.61×10”kPa，试用下述两种方法计算其体积。试比较哪种方法计算出来的体积与实测值更接近（已知实测值为28.5dm）。已知在该条件下NHs（g）的临界参数为T=405.6K，pe=1.13×10*kPavanderWaals气体常数为a=0.417Pam·mol-2,b=3.71×10-"m2.mol-1。（1）用vanderWaals气体状态方程式；（2）用压缩因子图。解（1）将vanderWaals方程改写为(6+RT)v+a-b=0V3力pp将NH,(g)的vanderWaals常数a=0.417Pa·m.mol-2,b=3.71X10-5m.mol-1及T=348Kp=1.61×10°kPa代人上式，利用一些数学软件（如Matlab）就可求出上述三次方程的解为Vm=1.684X 10-3m2.mol-1RT也可将vanderWaals方程改写为V.+6p+a/Va用送代法进行计算。以理想气体状态方程的计算值Vm=1.80×10-3m·mol-1作初值，代人上式右边计算得V.（1)=1.70×10-3m2·mol-1，再将此值代入上式右边计算，又得Vm（2）=1.68×10~3m2.mol-1，反复选代，经过5次选代得到，Vm（5）=1.684×10-3m.mol-1。再继续选代，计算