
这种解法的前提是认为冰可以全部融化,致使水的温度下降,终态全部是水,但温度降至253K,这显然是不符合实际的,因此形成错误。假如I△H(水)(水温降至0C)I>△H(冰)(冰全部融化),则这种解法既简便、又合理。7绝例题1-11装置如图,始态时绝热298K298K加理想活塞两侧容积各为20dm,均充满热20dm20dm310'Pa10'Pa298K、105Pa的双原子分子理想气体。对左侧气室缓慢加热、直至左室气体压力1绝热理想活塞为2.0×105Pa。请分别以左室气体、右室气体和所有气体为系统,求此过程的Q、W、△U、△H。解解法一(1)以右室气体为系统因绝热,Q(右)一0。由于对左室气体加热是缓慢的,因此而引起的活塞右移可视为可逆压缩过程。根据绝热可逆过程方程先求V(右)。,VY—2V(右)PIV,(右) V力a10520 Xdm342X105= 12dma1W(右)=-1(piVi-p2Ve)r1L1. 4=1(10° × 20 × 10-3 -2 × 105 × 12 × 10-3)= 1. 1kJAU(右)=Q(右)一W(右)=1.1kJ△H(右)=YU(右)=(1.4×1.1)kJ=1.5kJ(2)以左室气体为系统右室体积缩小量就是左室体积增大量。.18

V.(左)=[20+(20---12)dm2=28dm由理想气体状态方程,其终态温度为:T(左)=Tip,V/p,V=[298×2×105×28×10-/(105×20×10")JK=834.4Kn=p,V,/RT=[105X20X10-3/(8.314X298)mol= 0.81molAU(左) = nCv.m(T(左) 一TD)5.0.81XX 8.314 X (834.4-298)2= 9. 0kJ× 9. 0jkJ = 12. 6kJAH(左)=YAU=5W(左)=—W(右)=1.1kJQ(左)一4U(左)十W(左)=10.0kJ(3)以所有气体为系统AU=AU(左)+4U(右)=(1.1+9.0)kJ=10.1kJAH=AH(左)+AH(右)=(1.5+12.6)kJ=14.1kJW=W(左)十W(右)=OQ=Q(左)+Q(右)=(10.0+0)kJ=10.0kJ以所有气体为系统时,系统中的一部分对另一部分所作的功就不再是系统与环境之间的能量交换形式。此时可直接依据总体积恒定而确定W=0。解法二以右室气体为系统由绝热可逆过程方程先求终态温度:DT(右)105298>2X 105.19
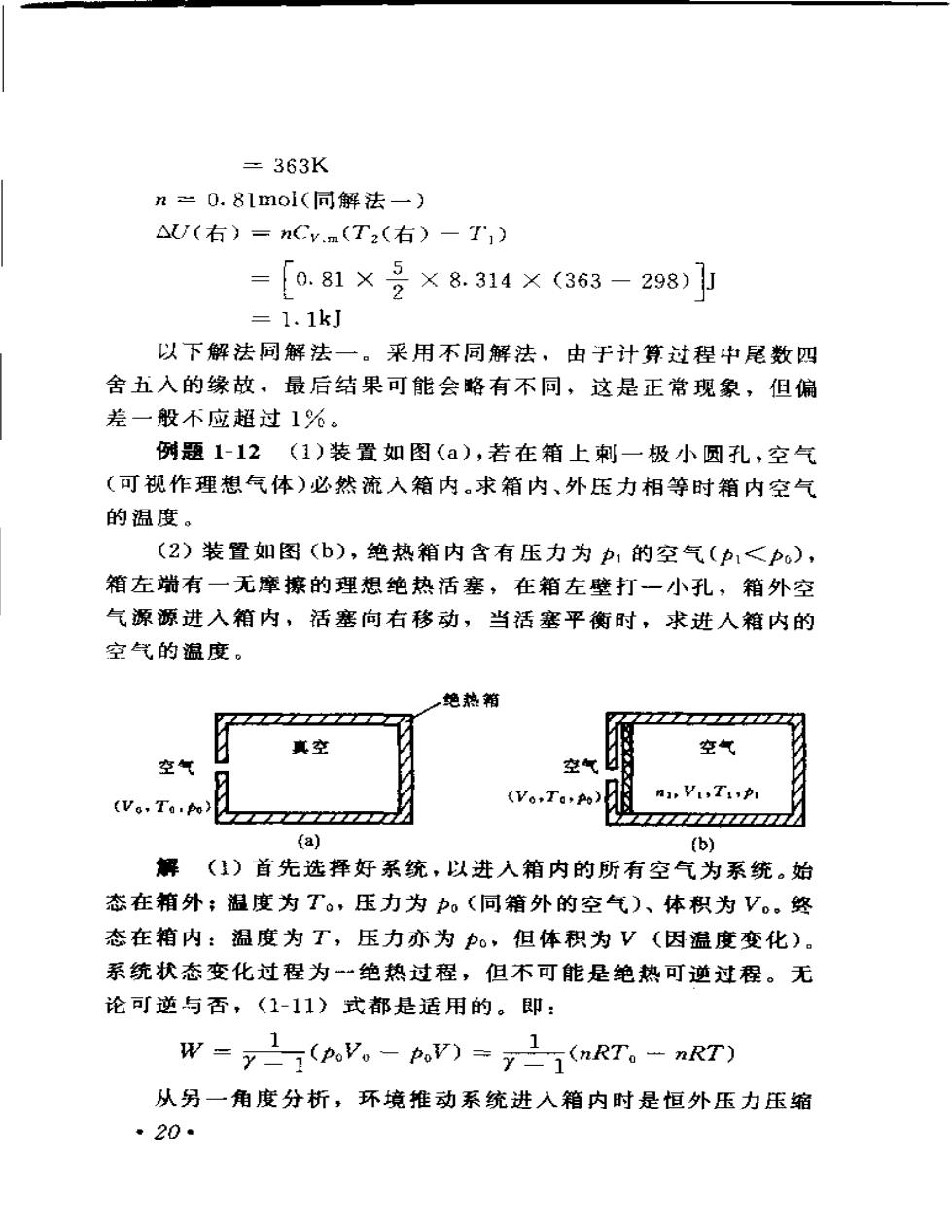
=363Kn=0.8lmol(同解法一)AU(右)=nCVmT2(右)一T)5=[o.81 ×X 8.314X(363-298)2= 1.1kJ以下解法同解法一。采用不同解法,由于计算过程中尾数四舍五入的缘故,最后结果可能会略有不同,这是正常现象,但偏差一般不应超过1%。例题1-12(1)装置如图(a),若在箱上刺一极小圆孔,空气(可视作理想气体)必然流入箱内。求箱内、外压力相等时箱内空气的温度。(2)装置如图(b),绝热箱内含有压力为的空气(pl<po),箱左端有一无摩擦的理想绝热活塞,在箱左壁打一小孔,箱外空气源源进入箱内,活塞向右移动,当活塞平衡时,求进人箱内的空气的温度。绝热箱真空空气空气以空气国An,Vi,Ti,p(Vo,Ta-po(Vo,Ta.po)(a)(b)解(1)首先选择好系统,以进入箱内的所有空气为系统。始态在箱外;温度为T。,压力为P。(同箱外的空气)、体积为V。终态在箱内:温度为T,压力亦为o,但体积为V(因温度变化)。系统状态变化过程为绝热过程,但不可能是绝热可逆过程。无论可逆与否,(1-11)式都是适用的。即:W -(poVo-poV) =-1(nRT。-nRT)从另一角度分析,环境推动系统进入箱内时是恒外压力压缩-20

过程,在箱外体积由V变到0。系统进人箱内后,由于箱内原先是真空,所以是自由膨胀过程。总功为:W=-p.V。=-nRT。两式结合:1(nRT。一nRT)—nRTylT=YT。(2)设进人箱内的所有空气为系统(n。)。始态在箱外(T。V。、P。);终态在箱内(T2、V2o)。终态时,活塞两边压力相等,且等于箱外空气压力。设箱内原有空气的物质的量为n,始态(T1、P、V),终态(Ta、Po、V)。箱内、外气体热容为Cv.t系统受到箱外空气(环境)的推动进人箱内,此为等外压力压缩过程,作功W。同时系统又对箱内原有气体(环境)作压缩功Wz,系统所作净功:W-W+W?整个过程为绝热,Q一0。W =- AU =- nCy.m(T2-T) =W, + W?又W = p(外)AV =(OV.)=-PV。=— n.RT。而W,等于箱内原有气体的压缩功的负值,即:W--W3W, =-AU, =- nCv.n(T:-T,)则W-W,+W,=--nRT。+niCvm(Ts-T)=-nCv.m(T,T.)T (+1)T。-浆(T - T)Cvn2箱内原有气体的压缩过程为一绝热可逆过程,故:T=121*

T - YT. -禁T[() -1例题1-13(1)试证明对遵守范德华方程的1mol实际气体来说,其等温可逆膨胀功可用下式求算(《物理化学简明教程》第一章习题10):Vr.? -b +W = RTIn v..+a[ V..?5OD(2)已知=T一力,求上述过程的△U、Q。awL(3)求上述系统在绝热自由膨胀过程中的温度变化。解(1)1mol实际气体的范德华状态方程为:p+)(V- 6) = RT所以RTa力=V.-bVm在等温可逆膨胀中:[p(外)d=[pdvW-RTIdJV-Vm.2- b= RTInVmi=6 +注意,只有可逆过程中或等压过程中,才能以系统压力力代替力(外)求算功。在其他过程中,切忌以力混淆力外)。RTa(2)=V.-6-VR%),= V.baTRT(),T()R一力:V2等温膨胀过程中求△U,只须将上式积分:22