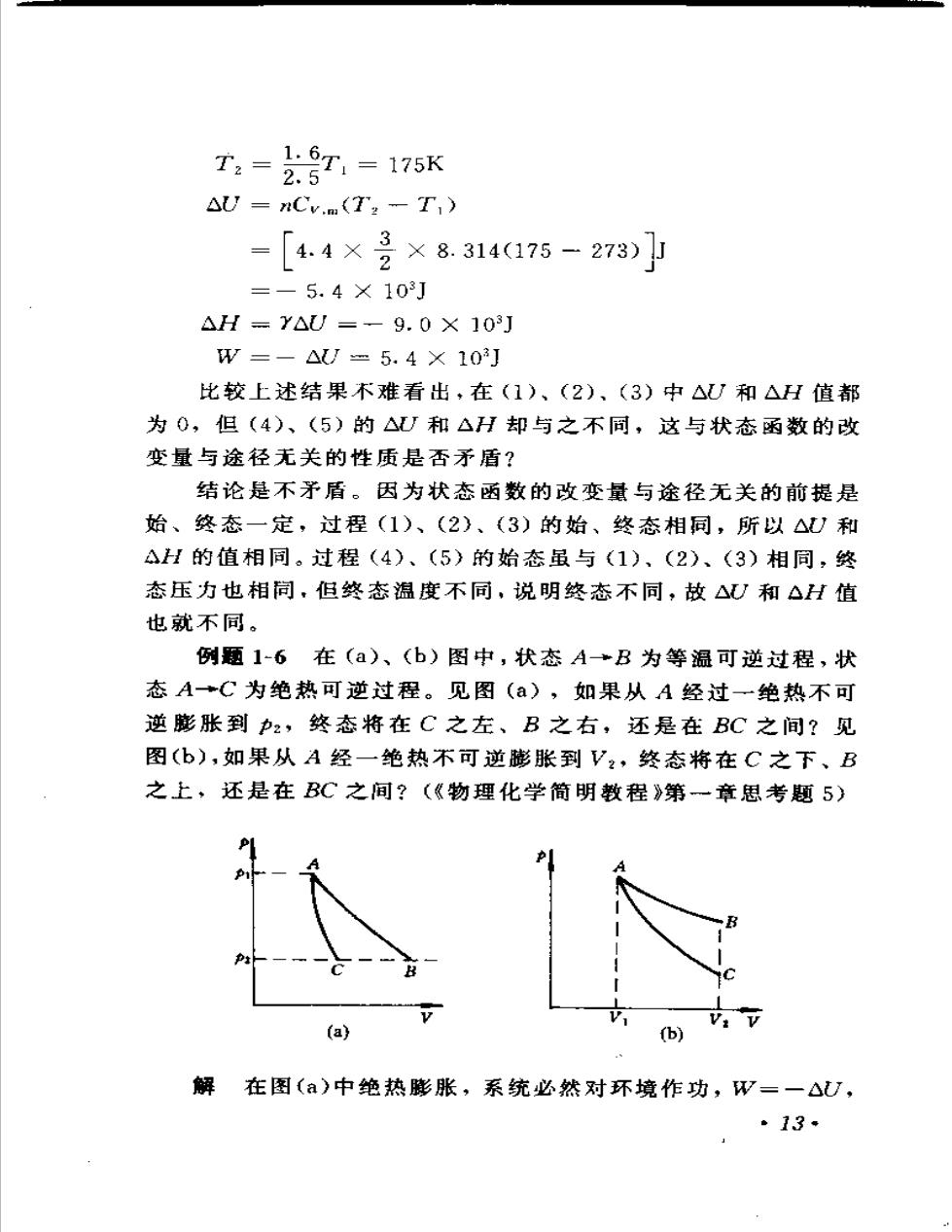
T2= TI = 175K2.5AU=nCV.m(TT)4.4×3×8.314(175- 273)2=-5.4X103JAH-YAU=-9.0X103JW=-△U-5.4X10J比较上述结果不难看出,在(1)、(2)、(3)中△U和△H值都为0,但(4)、(5)的△U和△H却与之不同,这与状态函数的改变量与途径无关的性质是否矛盾?结论是不矛盾。因为状态函数的改变量与途径无关的前提是始、终态一定,过程(1)、(2)、(3)的始、终态相同,所以△U和AH的值相同。过程(4)、(5)的始态虽与(1)、(2)、(3)相同,终态压为也相同,但终态温度不同,说明终态不同,故U和AH值也就不同。例题1-6在(a)、(b)图中,状态A-→B为等温可逆过程,状态A-→C为绝热可逆过程。见图(a),如果从A经过一绝热不可逆膨胀到P2,终态将在C之左、B之右,还是在BC之间?见图(b),如果从A经一绝热不可逆膨胀到V?,终态将在C之下、B之上,还是在BC之间?(《物理化学简明教程》第一章思考题5)PPHB-VV.V.V(a)(b)解在图(a)中绝热胀,系统必然对环境作功,W一一△U,·13*

使系统的内能减少,系统的温度必然下降,当终态压力与B相同时,终态体积一定小于B,即在B之左。绝热不可逆膨胀所作的功小于绝热可逆过程,即绝热不可逆膨胀的终态温度高于绝热可逆过程的终态温度,当终态压力与C相同时、终态体积一定大于C,即在C之右。综上所述,从A经绝热不可逆膨胀到力2时,其终态必在BC之间。同理,在图(b)中从A经绝热不可逆膨胀到V2,其终态亦必定在BC之间。例题1-710dm2氧气(可视为理想气体)由2.0×105Pa经绝热可逆膨胀至30dm,求W、Q、AU、△H。解该题特点是无法求算始、终态的温度。不少初学者只掌握根据温度变化来求算理想气体的△U和△H,遇到这类题目往往会感到无从下手,甚至认为题目所给条件不全。其实不然,关键在于灵活。Cpm=1.4.R,Cgm=ARY双原子分子理想气体:Cv.m一Cv.n22由绝热可逆过程方程P,Vi二pV2:p: = (V) b = [(%)* × 2. 0 × 10° ]pa = 4. 3 × 10~Pa因绝热,Q一0。1W=,=-(pV - pV)[。l(2. 0×10 ×10 ×10-3—4. 3×10*×30×10-)JL0.4=1.8 X 103JAU=-W=-1.8X10JAH =YAU =- 2. 5 × 103J例题1-8物质的量为n的理想气体从V1等温膨胀至V2,再等压冷至V1:然后等容加热使压力增加至P(恢复原状)。如图,请根据该循环导出理想气体C与Cv关系。解过程(1)是理想气体等温过程::14

A0(1)=-0由理想气体状态方程V,=P2V2一nRT1。过程(2)为等压过程,pQ(2) - nCPm(T2 - T)(3)W(2) = p2(V, - V2)(1)-p2V,—p2V2其中,p2V2=nRT,p2V,-nRT2。p?BCT(2)所以V、V.W(2)-nR(Tz-T)由热力学第一定律:△U(2) =Q(2) - W(2) nCm(T, - T) - nR(Tz - T,)过程(3)为等容过程:W(3)=0△U(3)=Q(3)=nCym(TT)系统经此三个过程后完成一个循环,恢复原始状态。故AU=0。AU=AU(1)÷AU(2)+AU(3)0 + (nCp.m -nR)(T-T)+nCvm(T-T)-0则Cn-CVmR此即理想气体C,与C的关系。推导理想气体C。与Cx关系的方法多种多样,其中较简便的方法是从恰的定义式出发,应用理想气体性质真接导出:H defU+pv微分得dH=dU十dpV)。对理想气体:dH=nCp.mdTdU - nCv.mdT.15

d(pV)= d(nRT)=nRdI所以Cem-Cym=R但是此法在本题中不能用,因为此法没有涉及本题指定的过程,不符合题意。解答本题时还有-一种常见的错误是仅依据过程(2):AU(2)= (nCp.m-nR)(T2-Ti)又根据理想气体特性:AU(2)=nCm(T,-T)所以nCp.m - nR = nCv.m即Cp.m-Cv.m=R这种推导尽管十分简便,但违背了题目的原意,也是不恰当的。例题1-9(1)1mol水在373K、pe下全部蒸发为水蒸气,求该过程的W、Q、△U、△H。已知水的汽化热为40.7kJ·mol1,(2)若是1mol、373K、p的水向真空蒸发,变成同温同压的水蒸气,结果如何?(水蒸气可视为理想气体)解(1)相变在等温、等压下进行,且只做体积功:AH =Q,=40.7kJW =pe (V- V) ~ p V,= RT = (8. 314 × 373)J=3.10kJAU =Q,-W=(40.7-3.10)kJ=37.6kJ(2)该相变向真空进行,为不可逆相变,力(外)一0。W=0由于(2)的始、终态同(1),所以△U和△H的值必然同(1)。AU=37.6kJ,AH= 40.7kJQ=AU+W=AU=37.6kJ所谓相变热是指等温等压、只做体积功的条件下,相变过程:16-

的热效应,即△H值。防止忽略条件,将相变热简单理解为相变过程的热效应。如(2)中,不符合上述条件的相变过程热效应不等于相变热,后者是状态函数改变量,仅与始、终态有关,而前者不是状态函数改变量,与变化途径有关。例题1-10将100g、40C的水与100g、0℃的冰在杜瓦瓶中混合,求平衡后的状态及此过程的H。已知冰的熔化热为335Jg-,水的比热为4.18J*g~1.K-1。解杜瓦瓶是等压绝热容器。取瓶内所有的水和冰为系统,则Q,一△H=0(只做体积功)。若冰能全部融化:△H(冰)=(335×100)J=33.5kJ:若水温降至0C:△H(水)=-(100×4.18×40)J16.7kJ;系统总恰变:△H=△H(冰)+△H(水)=16.8kJ>0。该结果说明,若完成上述过程,系统必须吸热,这与题意绝热不符。所以实际情况只可能有部分冰融化,平衡后的状态必然是0的冰水混合物。设融化的冰为mg:AH=AH(冰)+AH(水)=(m×335-16.7×10)J=0解得m=50即平衡后状态为50g冰与150g水在0℃时的混合物,此过程的AH=0.对于该题常见的一种错误解法如下。设终态温度为T2:AHAH(冰)+AH水)=(335×100)J+[4.18×100(T2/K-273)J+[4.18×100×(T/K-313)J=0解得12-253K.17