
第一节周期信号分析 、 三角函数形式的傅里叶级数 用完备正交函数集{1,cosn@,t,sin no t,n=1,2,3,:…,∞} 对周期信号分解,即可得到周期信号的傅里叶展开式。 进行傅立叶展开的周期函数f(t)必须满足狄里赫利 (irichlet)条件,即在周期,4+T】内,函数 f (t) 1)若有间断点存在,则间断点数目必须有限; 2)极大值和极小值数目应该是有限个; 3》应是绝对可积的,即∫Ft< 在工程实践中所遇到的周期信号一般都满足狄里赫利条 件

第一节周期信号分析 周期信号f)的三角级数形式的傅立叶展开式 f(1)=ao a cos@t+a,cos 2@t+...+b sin t+b,sin 20 t+... =d+(d,cosnon+b,sin non) (≤t≤t+T 其中, 14f0d f(t)cosnotdt (n=1,2,3,…,o) f(t)sin notdt
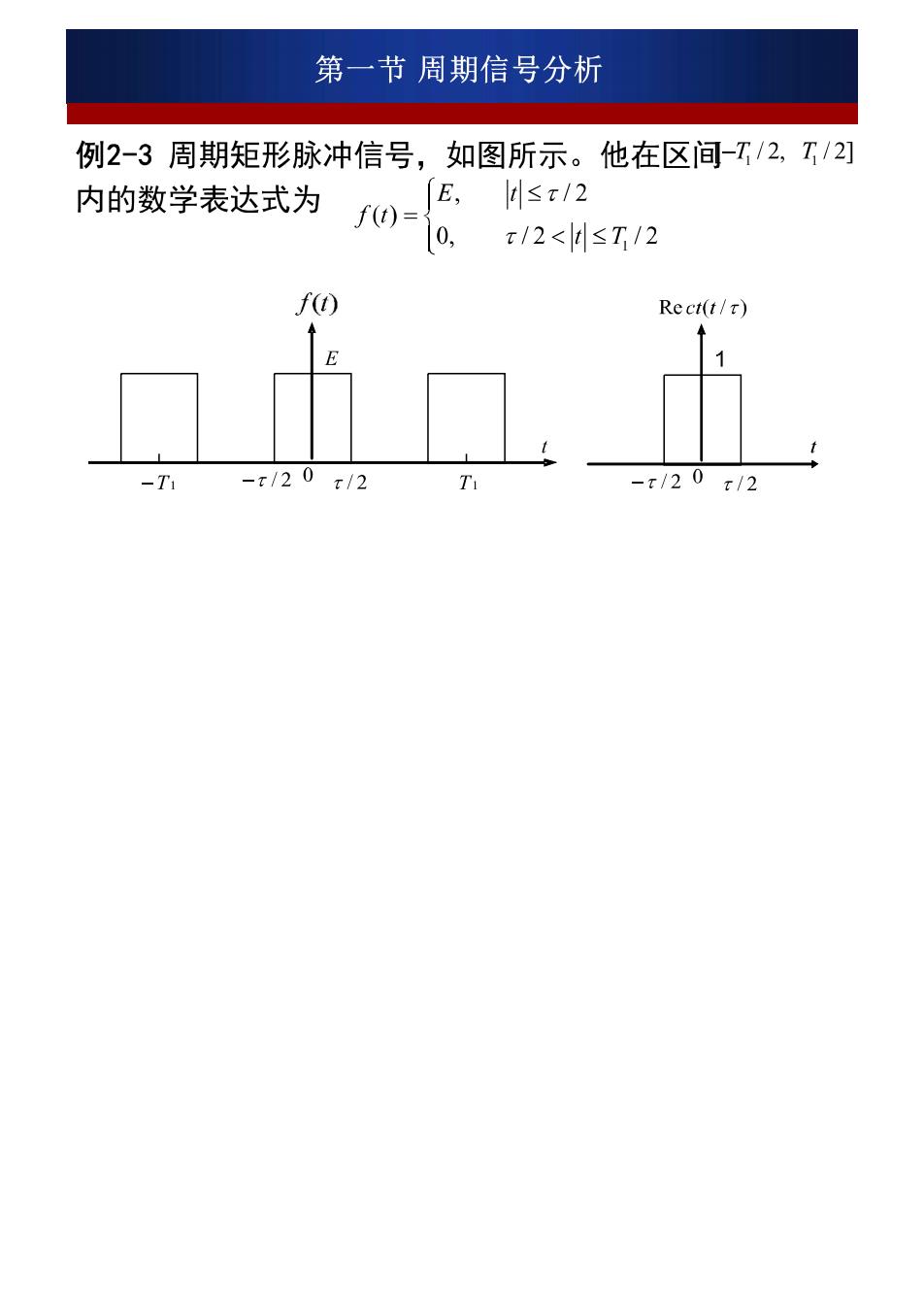
第一节周期信号分析 例2-3周期矩形脉冲信号,如图所示。他在区间-T/2,T/2] 内的数学表达式为f0 E,≤x/2 10, x/2<≤T/2 f() Rect(t/r) -/20x/2 T -x/20r/2

第一节周期信号分析 二、指数函数形式的傅里叶级数 在,4+T]内可以用指数函数集来表示周期信号f(t)。 f0=∑Fa)em:i≤1≤i+T 式中 F(n@)=
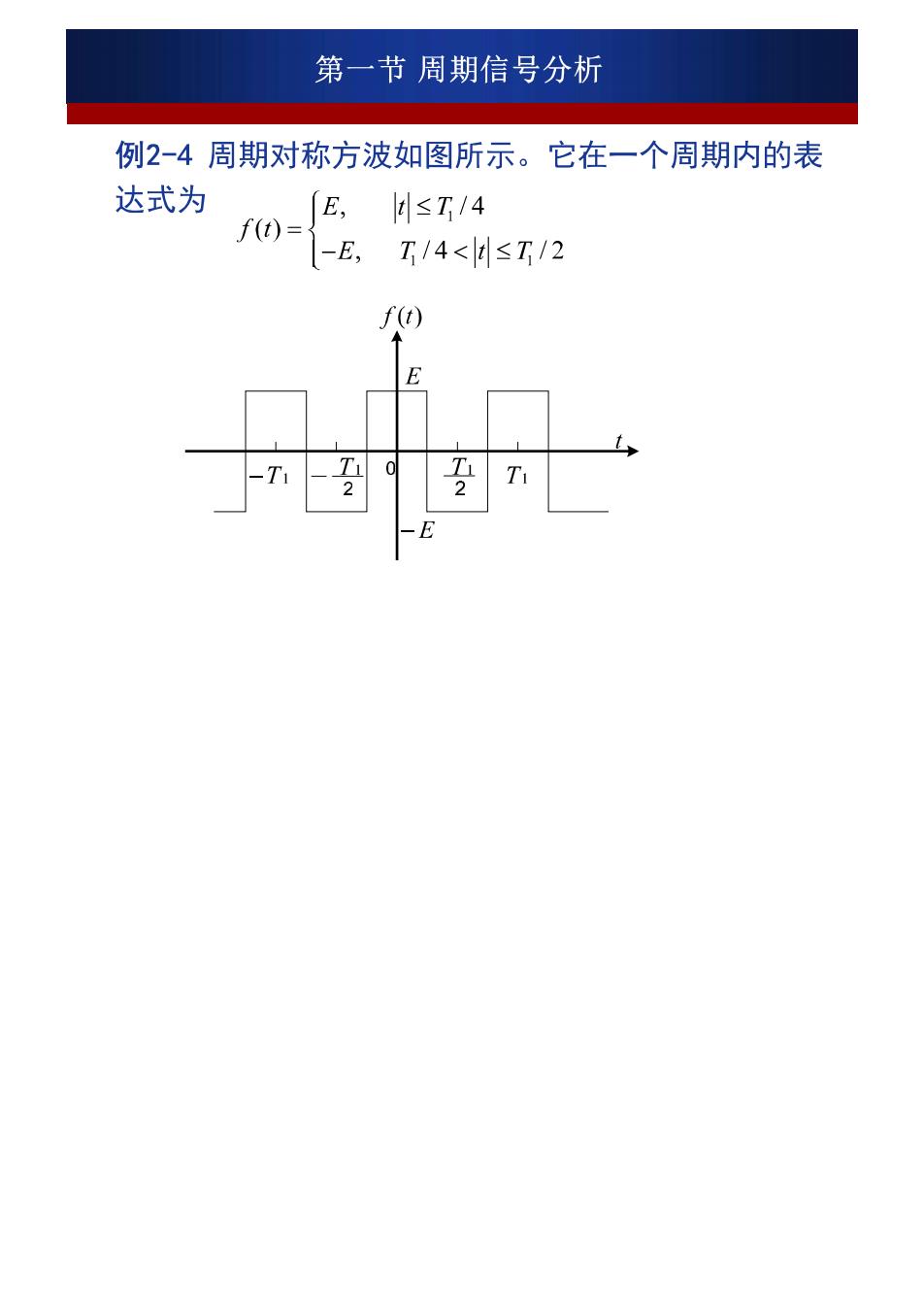
第一节周期信号分析 例2-4周期对称方波如图所示。它在一个周期内的表 达式为 E,4≤T/4 f(t)= -E,T14<4≤T/2 +=