
石河子大学师范学院物理系 近代物理实验讲义 验证快速电子的动量与动能的相对论关系 爱因斯坦于1905年提出了狭义相对论,根据相对论能量一动量关系式,“无质最”粒子 是能够存在的,且无静止质量的粒子将以光速传播。而在经典力学中,一个没有质量(即静 质量)的粒子慨没有能量,也没有动量,也没有任何其它可测量的性质,它什么也不是。对 于快速运动的电子,我们可以设计测最其动量与动能大小的实验,从而验证动量与动能的相 对论关系。本实验结果表明狭义相对论的动量和能量的关系式正确地描述了快速运动电子的 动量与能量关系,而若用牛倾运动定律来描述,明显不符合实验结果。 【实验目的】 1.通过对快速电子的动量及动能值的同时测定来验证动量和动能之间的相对论关系。 2.了解β磁谱仪测量原理和闪烁记数器的使用方法。 3.掌握快速电子动能的测量及一些实验数据处理的思想方法。 【实验器材】 实验装置主要由以下部分组成:①真空、非真空半圆聚焦磁谱仪:②放射源S0Y (强度≈1毫居里),定标用y放射源7cs和0co(强度2微居里):③200um铝窗Nal(T) 闪烁探头:④数据处理计算软件:⑤高压电源、放大器、多道脉冲幅度分析器。 【实验原理】 经典力学总结了低速物理的运动规律,它反映了牛顿的绝对时空观:认为时间和空间是 两个独立的观念,彼此之间没有联系:同一物体在不同惯性参照系中观察到的运动学量(如 坐标、速度)可通过伽利略变换而互相联系。这就是力学相对性原理:一切力学规律在伽利 略变换下是不变的。 19世纪末至20世纪初,人们试图将伽利略变换和力学相对性原理推广到电磁学和光学时 遇到了困难:实验证明对高速运动的物体伽利略变换是不正确的,实验还证明在所有惯性参 照系中光在真空中的传播速度为同一常数。在此基础上,爱因斯坦于1905年提出了狭义相对 论,并据此导出从一个惯性系到另一个惯性系的变换方程即洛伦兹变换”。 在洛伦兹变换下,静止质量为m,速度为的物体,狭义相对论定义的动量即为: p-"=m (1-1) 1
石河子大学师范学院物理系 近代物理实验讲义 验证快速电子的动量与动能的相对论关系 爱因斯坦于 1905 年提出了狭义相对论,根据相对论能量-动量关系式,“无质量”粒子 是能够存在的,且无静止质量的粒子将以光速传播。而在经典力学中,一个没有质量(即静 质量)的粒子既没有能量,也没有动量,也没有任何其它可测量的性质,它什么也不是。对 于快速运动的电子,我们可以设计测量其动量与动能大小的实验,从而验证动量与动能的相 对论关系。本实验结果表明狭义相对论的动量和能量的关系式正确地描述了快速运动电子的 动量与能量关系,而若用牛顿运动定律来描述,明显不符合实验结果。 【实验目的】 1.通过对快速电子的动量及动能值的同时测定来验证动量和动能之间的相对论关系。 2. 了解β磁谱仪测量原理和闪烁记数器的使用方法。 3. 掌握快速电子动能的测量及一些实验数据处理的思想方法。 【实验器材】 实验装置主要由以下部分组成:① 真空、非真空半圆聚焦磁谱仪;② 放射源90Sr- 90Y (强度≈1毫居里),定标用γ 放射源137 Cs和60Co(强度≈2微居里);③ 200µm铝窗NaI(Tl) 闪烁探头;④ 数据处理计算软件;⑤ 高压电源、放大器、多道脉冲幅度分析器。. 【实验原理】 经典力学总结了低速物理的运动规律,它反映了牛顿的绝对时空观:认为时间和空间是 两个独立的观念,彼此之间没有联系;同一物体在不同惯性参照系中观察到的运动学量(如 坐标、速度)可通过伽利略变换而互相联系。这就是力学相对性原理:一切力学规律在伽利 略变换下是不变的。 19世纪末至20世纪初,人们试图将伽利略变换和力学相对性原理推广到电磁学和光学时 遇到了困难;实验证明对高速运动的物体伽利略变换是不正确的,实验还证明在所有惯性参 照系中光在真空中的传播速度为同一常数。在此基础上,爱因斯坦于1905年提出了狭义相对 论,并据此导出从一个惯性系到另一个惯性系的变换方程即“洛伦兹变换”。 在洛伦兹变换下,静止质量为m0,速度为v的物体,狭义相对论定义的动量p为: 0 2 1 m p v β = − = mv (1-1) 1

石河子大学师范学院物理系 近代物理实验讲义 式中m=m。/√1-B2,B=v/c,相对论的能量E为: E=mc2 (1-2) 这就是著名的质能关系,mc2是运动物体的总能量,当物体静止时v=0,物体的能量 为E。=mc2称为静止能量:两者之差为物体的动能E,即 E.-me'-me'm'() 1 (1-3) 当B<1时,式(1-3)可展开为 (1-4) 2 mo 即得经典力学中的动最一能最关系。 根据式(1)和(12)可得: E2-c2p2=E2 (1-5) 这就是狭义相对论的动量与能量关系,而动能与动量的关系为: Ex=E-Eo=c'p2+moc-moc2 (1-6) 这就是我们要验证的狭义相对论的动量与动能的关系。对高速电子其关系如下图1所 示,图中pc用MeV作单位,电子的m,c2=0.511MeP,式(1-4)可化为: 6器 p'c2 相时论 0.5 ,5 201 pe[Mev] 图1高速电子的动量和动能的关系 【实验内容及步骤】 1.给闪烁探测器定标 (1)检查仪器线路连接是否正确,然后开启高压电源,开始工作: 2
石河子大学师范学院物理系 近代物理实验讲义 式中 m m / 1 , v / c 2 = 0 − β β = ,相对论的能量 E 为: E = mc 2 (1-2) 这就是著名的质能关系, 是运动物体的总能量,当物体静止时 ,物体的能量 为 称为静止能量;两者之差为物体的动能 ,即 2 mc v = 0 2 0 0 E = m c Ek 1) 1 1 ( 2 2 0 2 0 2 − − = − = β E mc m c m c k (1-3) 当 β << 1时,式(1-3)可展开为 2 2 2 2 2 0 0 2 0 0 0 1 111 (1 ) 2 222 k v p E m c m c m v m v c m = + +L − ≈ = =2 (1-4) 即得经典力学中的动量—能量关系。 根据式(1-1)和(1-2)可得: (1-5) 2 0 2 2 2 E − c p = E 这就是狭义相对论的动量与能量关系,而动能与动量的关系为: 2 0 2 4 0 2 2 0 E E E c p m c m c k = − = + − (1-6) 这就是我们要验证的狭义相对论的动量与动能的关系。对高速电子其关系如下图 1 所 示,图中 pc 用 MeV 作单位,电子的 m0c 2 = 0.511MeV ,式(1-4)可化为: 2 2 0.511 1 2 2 2 0 2 2 × = = p c m c p c Ek 以利于计算。 图1 高速电子的动量和动能的关系 【实验内容及步骤】 1. 给闪烁探测器定标 (1) 检查仪器线路连接是否正确,然后开启高压电源,开始工作; 2

石河子大学师范学院物理系 近代物理实验讲义 (2)打开"C0Y定标源的盖子,移动闪烁探测器使其狭缝对准Co源的出射孔并开始记 数测量: (3)调整加到闪烁探测器上的高压和放大数值,使测得的Co的1.33MV蜂位道数在 个比较合理的位置(建议:在多道脉冲分析器总道数的50%一70%之间,这样既可以保证测 量高能β粒子(1.8~1.9MV)时不越出量程范围,又充分利用多道分析器的有效探测范围): (4)选择好高压和放大数值后,稳定10~20分钟: (5)正式开始对Nal(T)闪烁探测器进行能量定标,首先测量Co的r能谱,当1.33MeV 光电蜂的峰顶记数达到1000以上后(尽量减少统计涨落带来的误差),对能谱进行数据分析, 记录下1,17和1.33MeV两个光电峰在多道能谱分析器上对应的道数CH、CHa: (6)移开探测器,关上C0Y定标源的盖子,然后打开B7C5Y定标源的盖子并移动闪烁 探测器使其狭缝对准7C源的出射孔并开始记数测量,等0.66]MV光电峰的峰顶记数达到 10O0后对能谱进行数据分析,记录下0.184MeV反散射峰和0.661MeV光电峰在多道能谱分析 器上对应的道数CH、CH: 2.测量快速电子的动量和动能 ()关上CsY定标源,打开机械泵抽真空(机械泵正常运转2一3分钟即可停止工作): (②)盖上有机玻璃罩,打开源的盖子开始测量快速电子的动量和动能,探测器与B源的 距离△x最近要大于9cm、最远要小于24cm,保证获得动能范围0.4~18MeV的电子 (③)选定探测器位置后开始逐个测量单能电子的能峰,记下峰位道数CH和相应的位置 坐标x: (④全部数据测量完毕后关闭那源及仪器电源,进行数据处理和计算 3.数据处理 ()能量定标:用最小二乘法拟合E=a+b×CH,求得a和b。 (2)B粒子动能的测量:利用所得拟合公式E=a+b×CH,求在不同x处B粒子的动能。 粒子与物质相互作用是一个很复杂的问题,如何对其损失的能量进行必要的修正十分 重要。 ①β粒子在铝膜中的能量损失修正 在计算B粒子动能时还需要对粒子穿过铝膜(220m,其中200um为Nal(T)晶体的 铝膜密封层厚度,20m为反射层的铝膜厚度)时的动能子以修正,计算方法如下。 设B粒子在铝膜中穿越△x的动能损失为△E,则: (1-7) dp
石河子大学师范学院物理系 近代物理实验讲义 (2) 打开 γ定标源的盖子,移动闪烁探测器使其狭缝对准 源的出射孔并开始记 数测量; Co 60 Co 60 (3) 调整加到闪烁探测器上的高压和放大数值,使测得的 的1.33MeV峰位道数在一 个比较合理的位置(建议:在多道脉冲分析器总道数的50%~70%之间,这样既可以保证测 量高能β粒子(1.8~1.9MeV)时不越出量程范围,又充分利用多道分析器的有效探测范围); Co 60 (4) 选择好高压和放大数值后,稳定10~20分钟; (5) 正式开始对NaI(Tl)闪烁探测器进行能量定标,首先测量 的γ能谱,当1.33MeV 光电峰的峰顶记数达到1000以上后(尽量减少统计涨落带来的误差),对能谱进行数据分析, 记录下1.17和1.33MeV两个光电峰在多道能谱分析器上对应的道数CH Co 60 3、CH4; (6) 移开探测器,关上 γ定标源的盖子,然后打开 γ定标源的盖子并移动闪烁 探测器使其狭缝对准 源的出射孔并开始记数测量,等0.661MeV光电峰的峰顶记数达到 1000后对能谱进行数据分析,记录下0.184MeV反散射峰和0.661 MeV光电峰在多道能谱分析 器上对应的道数CH Co 60 Cs 137 Cs 137 1、CH2; 2. 测量快速电子的动量和动能 (1) 关上137Cs γ定标源,打开机械泵抽真空(机械泵正常运转2~3分钟即可停止工作); (2) 盖上有机玻璃罩,打开β源的盖子开始测量快速电子的动量和动能,探测器与β源的 距离 ∆x 最近要大于9cm、最远要小于24cm,保证获得动能范围0.4~1.8MeV的电子; (3) 选定探测器位置后开始逐个测量单能电子的能峰,记下峰位道数CH和相应的位置 坐标x; (4) 全部数据测量完毕后关闭β源及仪器电源,进行数据处理和计算。 3. 数据处理 (1) 能量定标:用最小二乘法拟合 E = a + b×CH ,求得a和b。 (2) β粒子动能的测量:利用所得拟合公式 E = a + b×CH ,求在不同x处β粒子的动能。 粒子与物质相互作用是一个很复杂的问题,如何对其损失的能量进行必要的修正十分 重要。 ①β粒子在铝膜中的能量损失修正 在计算β粒子动能时还需要对粒子穿过铝膜( 220µm ,其中 200µm 为NaI(Tl)晶体的 铝膜密封层厚度, 20µm 为反射层的铝膜厚度)时的动能予以修正,计算方法如下。 设β粒子在铝膜中穿越 ∆x 的动能损失为 ∆E ,则: dE E x dxρ ∆ = ρ∆ (1-7) 3
石河子大学师范学院物理系 近代物理实验讲义 其中正(正<0)是铝对粒子的能量吸收系数,(p是铝的密度、 dk。d。 是关于E的函 数,不同E情况下E的取值可以道过计算得到。可设P=K(E),则AE=K(E)Ax 取△r→0,则B粒子穿过整个铝膜的能量损失为:E,-£=∫K(E本,即 E1=E2-K( (1-8) 其中,d为薄膜的厚度,E2为出射后的动能,E1为入射前的动能。由于实验探测到的是 经铝膜衰减后的动能,所以经公式(1-8)可计算出修正后的动能(即入射前的动能)。下表列出 了根据(1-8)求出的入射动能E,和出射动能E2之间的对应关系: Ei(Mev)E2(Mev)Ei(Mev)E2(Mev)Ei(Mev)E2(Mev) 0.317 0.20 0.887 0.800 1.489 1.400 0.360 0.250 0.937 0.850 1.536 1.450 0404 0300 0988 0900 1583 1500 0451 0.350 1.039 0.950 1.638 1550 0.497 0.400 1.09 1.000 1.685 1.600 0.545 0.450 1.137 1050 1.740 1650 0595 0500 1.184 1100 1787 1700 0.640 0.550 1.23 1.15 1.834 1.750 0.690 0.600 1.286 1.200 1.889 1.800 0740 0.650 1333 150 1026 1850 0.790 0.700 1.388 1.300 1.991 1.900 0.840 0.750 1.435 1.350 2.038 1.950 ②B粒子在有机塑料薄膜中的能量损失修正 实验表明封装真空室的有机塑料薄膜对B粒子存在一定的能量吸收,尤其对小于0.4MV 的邹粒子吸收近0.02MV。由于塑料薄膜的厚度及物质组分难以测量,可采用实验的方法进 行修正。实验测量了不同能最下入射动能E,和出射动能E(单位均为MV的关系,采用分段 插值的方法进行计算。具体数据见下表: EMeV0.3820.5810.7m0.9731.1731.3671.5671.752 EMeV0.3650.5710.7700.9661.1661.3601.5571.747 ③由公式pc-V(E4+mc2)?-m2c计算pc的理论值。 ④由公式p=eBR计算B粒子在不同x处的动量p和pc的实验值。 ⑤根据步骤③和步骤4求得各实验点的相对不确定度。 (3)数据处理的计算方法和步骤(举例说明):
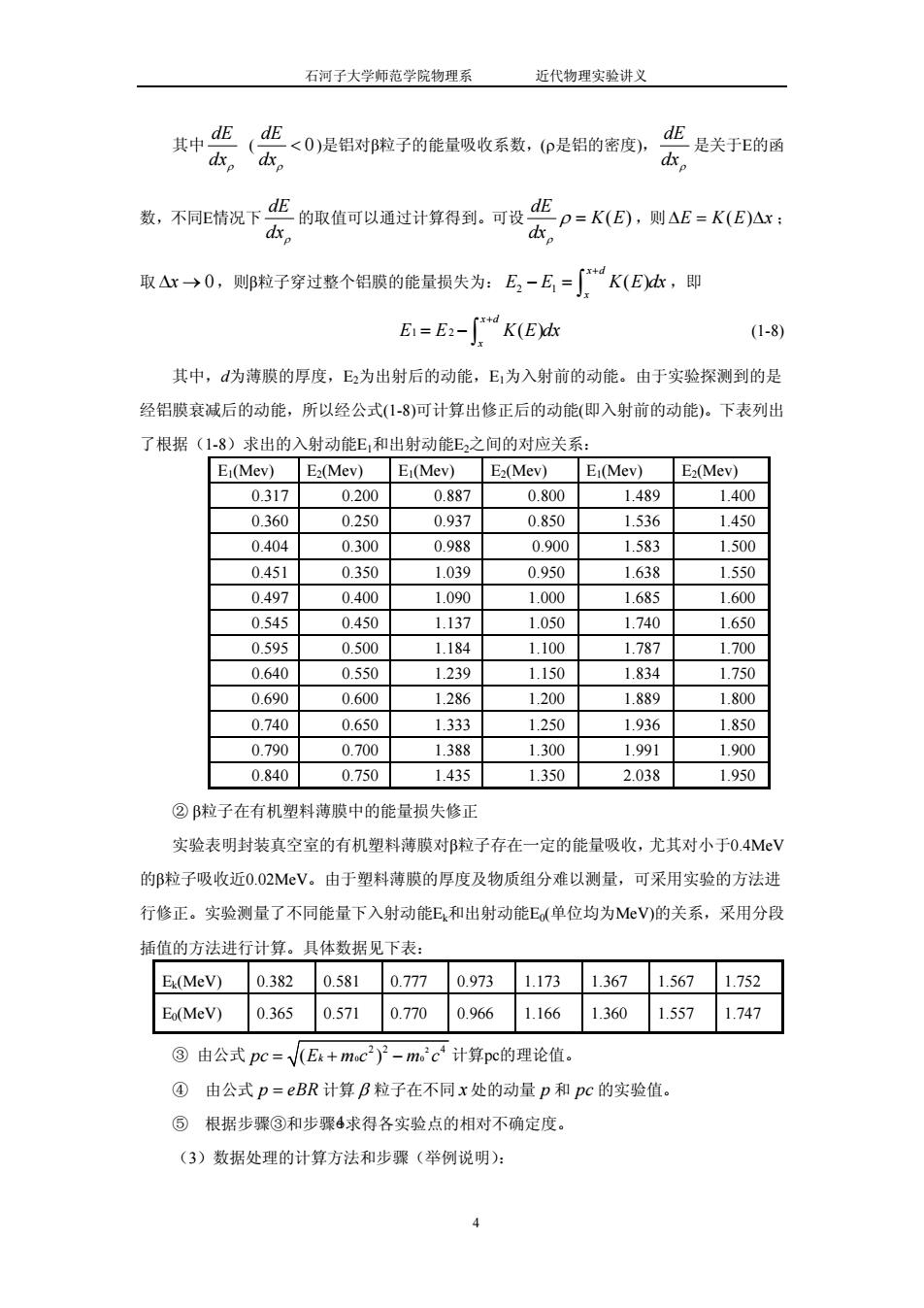
石河子大学师范学院物理系 近代物理实验讲义 其中 dE dxρ ( 0 dE dxρ < )是铝对β粒子的能量吸收系数,(ρ是铝的密度), dE dxρ 是关于E的函 数,不同E情况下 dE dxρ 的取值可以通过计算得到。可设 ( ) dE K E dxρ ρ = ,则 ∆ = E K E( )∆x ; 取 ∆ →x 0,则β粒子穿过整个铝膜的能量损失为: ,即 2 1 ( ) x d x E E K E dx + − = ∫ 1 2 ( ) (1-8) x d x E E K E d + = − ∫ x 其中,d为薄膜的厚度,E2为出射后的动能,E1为入射前的动能。由于实验探测到的是 经铝膜衰减后的动能,所以经公式(1-8)可计算出修正后的动能(即入射前的动能)。下表列出 了根据(1-8)求出的入射动能E1和出射动能E2之间的对应关系: E1(Mev) E2(Mev) E1(Mev) E2(Mev) E1(Mev) E2(Mev) 0.317 0.200 0.887 0.800 1.489 1.400 0.360 0.250 0.937 0.850 1.536 1.450 0.404 0.300 0.988 0.900 1.583 1.500 0.451 0.350 1.039 0.950 1.638 1.550 0.497 0.400 1.090 1.000 1.685 1.600 0.545 0.450 1.137 1.050 1.740 1.650 0.595 0.500 1.184 1.100 1.787 1.700 0.640 0.550 1.239 1.150 1.834 1.750 0.690 0.600 1.286 1.200 1.889 1.800 0.740 0.650 1.333 1.250 1.936 1.850 0.790 0.700 1.388 1.300 1.991 1.900 0.840 0.750 1.435 1.350 2.038 1.950 ② β粒子在有机塑料薄膜中的能量损失修正 实验表明封装真空室的有机塑料薄膜对β粒子存在一定的能量吸收,尤其对小于0.4MeV 的β粒子吸收近0.02MeV。由于塑料薄膜的厚度及物质组分难以测量,可采用实验的方法进 行修正。实验测量了不同能量下入射动能Ek和出射动能E0(单位均为MeV)的关系,采用分段 插值的方法进行计算。具体数据见下表: Ek(MeV) 0.382 0.581 0.777 0.973 1.173 1.367 1.567 1.752 E0(MeV) 0.365 0.571 0.770 0.966 1.166 1.360 1.557 1.747 ③ 由公式 2 0 0 2 2 4 pc = + ( ) Ek m c − m c p eBR 计算pc的理论值。 ④ 由公式 = 计算 β 粒子在不同 x 处的动量 p 和 pc 的实验值。 ⑤ 根据步骤③和步骤○4求得各实验点的相对不确定度。 (3)数据处理的计算方法和步骤(举例说明): 4

石河子大学师范学院物理系 近代物理实验讲义 设对探测器进行能量定标的数据如下: 能量(MeV)0.661 1.171.33 道数(CHD 158.8 283.2 321.0 实验测得当探测器位于25cm时的单能电子能峰道数为220,求该点所得β粒子的动能、 动量及误差,己知源位置坐标为10cm、平均磁场强度为642.8高斯(Gs)。 1)根据能量定标数据求定标曲线:己知:E1=0.661MeV,CH1=158.8: E2=1.17MeV,CH2=283.2:E3=1.33MeV,CH3=321.0:根据最小二乘法原理用线 性拟合的方法求能最E和道数CH之间的关系: E=a+bxCH 可以推导,其中: a=∑c∑E-∑CH-∑Ch-E b=A2CH-E)-∑CH-∑ A=n∑CH-(∑CH 代入上述公式计算可得:E=0.00877+0.0041CH 2)求郑粒子动能 对于x=25cm处的B粒子: ①将其道数220代入求得的定标曲线,得动能E=0.9108MV,注意:此为粒子穿过 计220m厚铝膜后的出射动能,需要进行能量修正: ②在前面所给出的穿过铝膜前后的入射动能E和出射动能E2之间的对应关系数据表中 取E2=0.9108MeV前后两点作线形插值,求出对应于出射动能E20.9108MeV的入射动能 E1=0.9990MeV E:(Mev)E2(Mev) 0.988 0.900 1.039 0.950 ③上一步求得的E为粒子穿过封装真空室的有机塑料薄膜后的出射动能E,需要再次 进行能量修正求出之前的入射动能E,同上面一步,取E一0.9990MV前后两点作线形插值, 求出对应于出射动能E=0.9990McV的入射动能E=1.006MeV: E(MeV) 0.9731.173 0.9661.166
石河子大学师范学院物理系 近代物理实验讲义 设对探测器进行能量定标的数据如下: 能量(MeV) 0.661 1.17 1.33 道数(CH) 158.8 283.2 321.0 实验测得当探测器位于25cm时的单能电子能峰道数为220,求该点所得β粒子的动能、 动量及误差,已知β源位置坐标为10cm、平均磁场强度为642.8高斯(Gs)。 1) 根据能量定标数据求定标曲线:已知; E M 1 1 = 0.661 eV,CH =158.8 ; E M 2 2 = = 1.17 eV ,CH 283.2 ; E M 3 =1.33 eV,CH 3 = 321.0 ;根据最小二乘法原理用线 性拟合的方法求能量E和道数CH之间的关系: E a = + ×b CH 可以推导,其中: 1 2 [ ( i i i i i i i i a C = ⋅ H E − CH ⋅ CH ∆ ∑ ∑ ∑ ∑ ⋅ Ei)] 1 [ ( i i) i i i i b n = ⋅ CH E − CH ⋅ E ∆ ∑ ∑ ] i ∑ H 2 2 i i ( ) i i ∆ = n C ∑ ∑ H − CH 代入上述公式计算可得: E C = + 0.00877 0.0041⋅ 2)求β粒子动能 对于x=25cm处的β粒子: ①将其道数220代入求得的定标曲线,得动能E2=0.9108MeV,注意:此为β粒子穿过总 计 220µm 厚铝膜后的出射动能,需要进行能量修正; ②在前面所给出的穿过铝膜前后的入射动能E1和出射动能E2之间的对应关系数据表中 取E2=0.9108MeV前后两点作线形插值,求出对应于出射动能E2=0.9108MeV的入射动能 E1=0.9990MeV E1(Mev) E2(Mev) 0.988 0.900 1.039 0.950 ③上一步求得的E1为β粒子穿过封装真空室的有机塑料薄膜后的出射动能E0,需要再次 进行能量修正求出之前的入射动能Ek,同上面一步,取E0=0.9990MeV前后两点作线形插值, 求出对应于出射动能E0=0.9990MeV的入射动能Ek=1.006MeV; Ek(MeV) 0.973 1.173 E0(MeV) 0.966 1.166 5