
二、光电效应与光子学说 光 1900年,Lenard在Hertzi和 Hallwachs实验的基础上,证明了 电子 金属在紫外光照射下会发射电 真空石英管 子,这就是光电效应。 实验表明: (1)光电流的大小与光强有关(频率合适); (2)产生光电效应的光有频率阈值ν。(与材料有关); (3)光电效应产生的光电子动能与ν有关,与光强无关; (4)光电效应的响应时间小于纳秒量级。 经典理论对现象的产生能够理解,也能理解光电流的大小与光强 有关,但无法解释其他实验规律
二、光电效应与光子学说 1900年,Lenard 在Hertz 和 Hallwachs实验的基础上,证明了 金属在紫外光照射下会发射电 子,这就是光电效应。 实验表明: (1)光电流的大小与光强有关 (频率合适); (2)产生光电效应的光有频率阈值 ν0 (与材料有关); (3)光电效应产生的光电子动能与 ν有关,与光强无关 ; (4)光电效应的响应时间小于纳秒量级。 经典理论对现象的产生能够理解,也能理解光电流的大小与光强 有关,但无法解释其他实验规律

1905年,Einstein:提出光量子学说一光具有粒子性。 Planck-Einstein关系式: E=hv p=h/ Einstein光电效应公式: 1 hv=W+二1 2 .2 W为金属的脱出功。 斜率h(普朗克常量) 频率与截止电压为线性关系: hv=W+evo
1905年,Einstein提出光量子学说―光具有粒子性。 Planck-Einstein关系式: ⎩⎨⎧ == λ νhp / hE 2 2 1 vmWhν += e Einstein光电效应公式: W为金属的脱出功。 0 ν = + eVWh 频率与截止电压为线性关系:
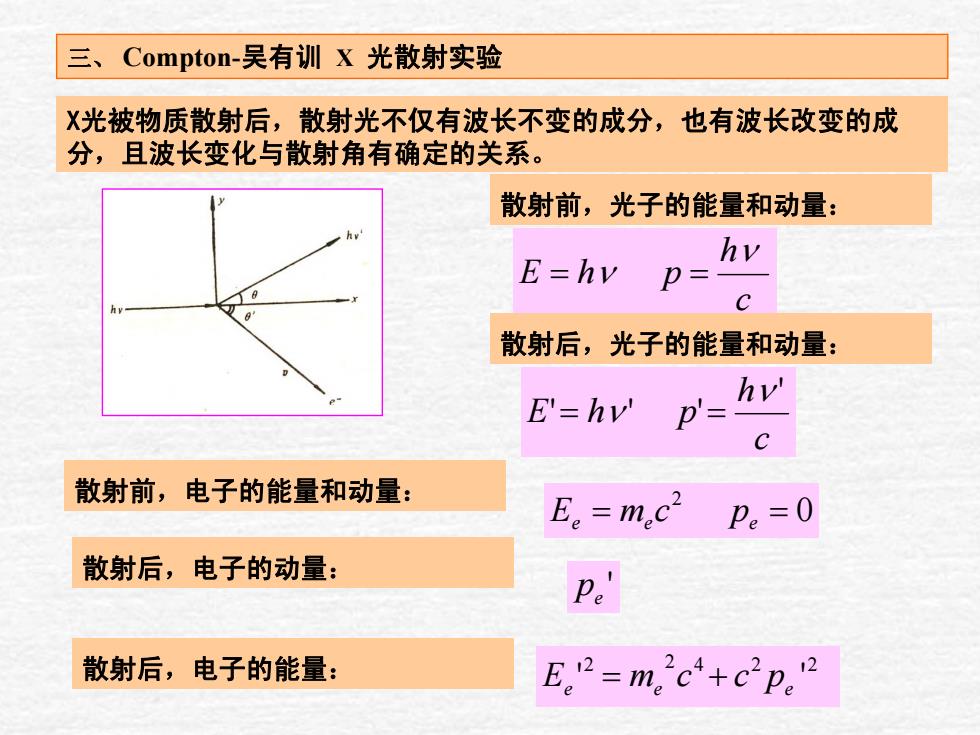
三、Compton-吴有训X光散射实验 X光被物质散射后,散射光不仅有波长不变的成分,也有波长改变的成 分,且波长变化与散射角有确定的关系。 散射前,光子的能量和动量: E=hv hv p= 散射后,光子的能量和动量: E'=hy p'= hv' 散射前,电子的能量和动量: E。=m,c2p。=0 散射后,电子的动量: P. 散射后,电子的能量: E。2=m.2c4+c2p.2
三、 Compton-吴有训 X 光散射实验 c h phE ν ν == 散射前,光子的能量和动量: 散射后,光子的能量和动量: 散射后,电子的动量: 散射前,电子的能量和动量: c h phE ' ''' ν ν == 0 2 = ee pcmE e = 2 2 224 ' ' ee += pccmE e 散射后,电子的能量: ' e p X光被物质散射后,散射光不仅有波长不变的成分,也有波长改变的成 分,且波长变化与散射角有确定的关系
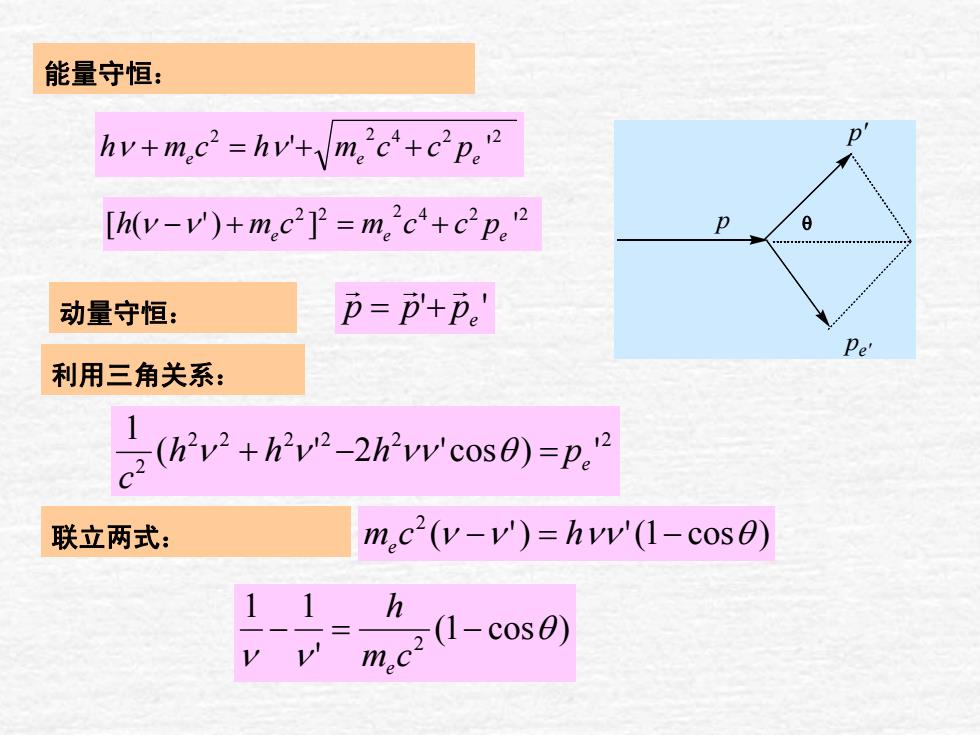
能量守恒: hv+mc2=hvmc+cp.2 [h(v-v)+mc2P=m'c+c'p.2 动量守恒: p=p'+p。' Pe 利用三角关系: 点v2+-2hros1=n 联立两式: m.c(v-v')=hvv'(1-cOse) .c(1-cos0) 1_1h
2 2 224 ' ' ν e ν e ++=+ pccmhcmh e 联立两式: 能量守恒: 动量守恒: 22222 2 2 ')cos'2'( 1 hhh pe c −+ θνννν = 22 2 224 ])'([ ' h νν e e +=+− pccmcm e )cos1(')'(2 ecm h −=− θνννν )cos1( ' 11 2 θ νν −=− cmhe p θ p' pe' '' ppp e G G G = + 利用三角关系:

得: 0=09 h 元-=h(1-cos) mc =451 故: 8=909 △2=2'-1= 2h。n20 sin (AA=2ksin2 m.c 2 0-2 0-135 Compton散射进一步从实验上证明了光子学 说;同时证明能量守恒、动量守恒在微观碰撞 事件中成立。 0 0.700 0.750
) 2 sin2( 2 sin 2 2 2 θ λ θ λλλ k cmhe =Δ ′ =− =Δ λλ −=− θ )cos1(' cm h e 得: 故: Compton散射进一步从实验上证明了光子学 说;同时证明能量守恒、动量守恒在微观碰撞 事件中成立