
Generating Functions
Generating Functions

Generating Functions: Enumerative Combinatorics "the most useful but most RICHARD P.STANLEY difficult to understand method (for counting)' CONCRETE MATHEMATICS AHAM KNUTH PATASHN "the most powerful way to deal with sequences of numbers,as far as anybody knows
“the most useful but most difficult to understand method (for counting)” Generating Functions: “the most powerful way to deal with sequences of numbers, as far as anybody knows

generate enumerate all subsets of {O,●,O} (x0+x2)(ax0+x2)(x0+x2) =2x020+x0xx1+20x'x0+20zlxI +x1x0x0+x1a0x1+x1x1a0+1xx1 (1+x)3=1+3a+3x2+x3 coefficient ofx:of k-subsets
{ , , } enumerate all subsets of generate (x0 + x1)(x0 + x1)(x0 + x1) = + + + + + + + x1 x0x0x0 x0x0x1 x0 x0 x1 x0 x1 x1 x0 x0 x1 x0 x1 x1 x0 x1 x1 x1 x1 (1 + x) 3 =1+3x + 3x2 + x3 coefficient of xk : # of k-subsets

O,O,O ●,●,0,●, ○,0,0,0,○} (1+x+x2+x3) (1+x+x2+x3+x4) (1+x+x2+x3+x4+x5) 1+3x+6x2+10x3+14x4+17x5+18x6 +17x7+14x8+10x9+6x10+3x11+x12
(1 + x + x2 + x3) (1 + x + x2 + x3 + x4) (1 + x + x2 + x3 + x4 + x5) { } , , , , , , , , , , , = 1+3x + 6x2 + 10x3 + 14x4 + 17x5 + 18x6 +17x7 + 14x8 + 10x9 + 6x10 + 3x11 + x12
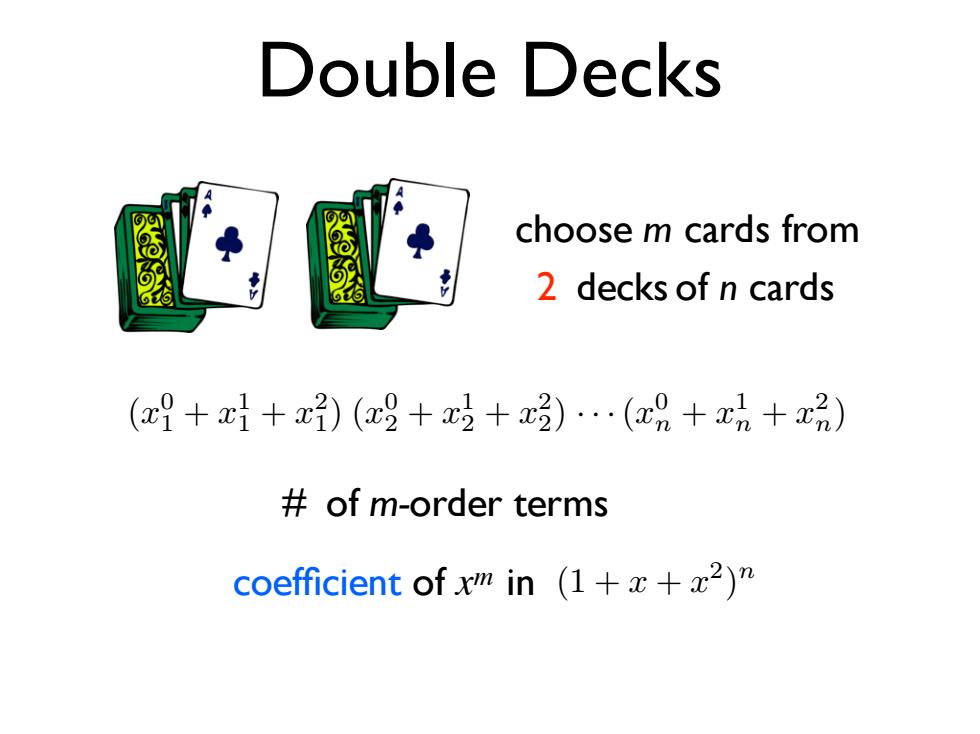
Double Decks choose m cards from 2 decks of n cards (9+1+x)(唱+吃+z)…(a%+xh+x品) of m-order terms coefficient of xm in (1+x+2)
Double Decks (x0 1 + x1 1 + x2 1) (x0 2 + x1 2 + x2 2) ···(x0 n + x1 n + x2 n) # of m-order terms (1 + x + x2) n coefficient of xm in 2 deck of s n cards choose m cards from