
高级机器学习( 2021秋季学期) 二、典型方法 主讲教师:詹德川
二、典型方法 主讲教师:詹德川 高级机器学习 (2021秋季学期)

线性模型 分类 回归 线性模型((linear model))试图学得一个通过属性的线性组合来进行预测的函数 f()=w1x1+w2x2+...+wdxd+b 向量形式:f(x)=wTx+b 简单、基本、可理解性好
线性模型 分类 回归 线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数 向量形式: 简单、基本、可理解性好

线性模型的变化 对于样例(x,y),y∈R,若希望线性模型的预测值逼近真实标记, 则得到线性回归模型y=wx+b 令预测值逼近y的衍生物? (3,93)ly=ewTx+b 30 若令ny=wTx+b (x2,2) 20 则得到对数线性回归 (x1,h) =血 (log-linear regression) 10 y=wTx+b 实际是在用ewTx+b逼近y x1, (2,站(3.g) 2
线性模型的变化 对于样例 若希望线性模型的预测值逼近真实标记, 则得到线性回归模型 令预测值逼近 y 的衍生物? 若令 则得到对数线性回归 (log-linear regression) 实际是在用 逼近 y

广义(generalized)线性模型 一般形式: y=91((wTc+b) T 单调可微的联系函数((link function) 令g()=ln(·)则得到对数线性回归 Iny wTx+b
广义(generalized)线性模型 一般形式: 单调可微的 联系函数 (link function) 令 则得到 对数线性回归 … …
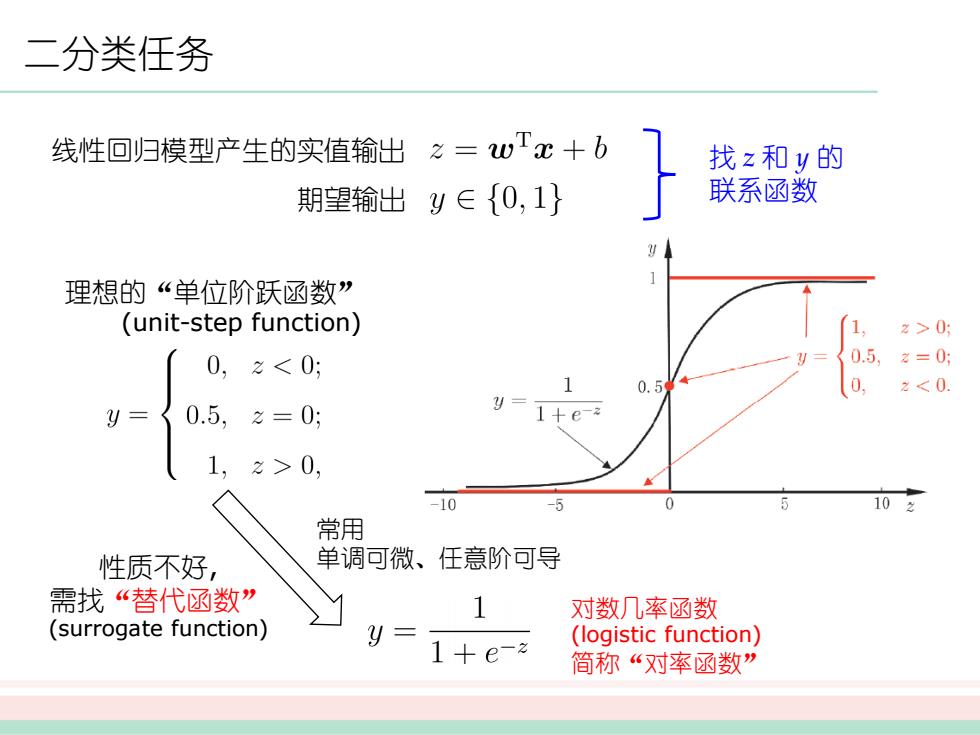
二分类任务 线性回归模型产生的实值输出之=wTx+b 找z和y的 期望输出y∈{0,1} 联系函数 理想的“单位阶跃函数” (unit-step function) 2>0: 0,2<0: 0.5 2=0: 0.5 0 2<0. y={0.5,之=0 1+e- 1,z>0, -10 -5 10 常用 性质不好, 单调可微、任意阶可导 需找“替代函数” 1 对数几率函数 (surrogate function) y= 1+e-2 (logistic function) 简称“对率函数
二分类任务 线性回归模型产生的实值输出 期望输出 找 z 和 y 的 联系函数 理想的“单位阶跃函数” (unit-step function) 性质不好, 需找“替代函数” (surrogate function) 常用 单调可微、任意阶可导 对数几率函数 (logistic function) 简称“对率函数