
§8-1寡头垄断企业的静态竟争及其博弃模型 二、古诺产量竞争模型 ⅡΠ(qq)=qp(qtq-c=qila-(q+q)-c 若一对战略(s*,S*)是纳什均衡,则对每个参与者1,s*应满足 u(S*,S*)≥山(S,S*) 上式对s中每一个可选战略s都成立。在古诺的双寡头垄断模型中,上面的 条件可具体表述为:若一对产出组合(q*,4*)为纳什均衡,则对每一个 企业i,q*应为下面最大化问题的解: maxπ,(q,4,)=maxq.a-(q,+q,)-c] 03q;<oo 0≤q,≤0 设q*<a-c, 企业最优化问题的一阶条件为: 6
6 §8-1 寡头垄断企业的静态竞争及其博弈模型 二、古诺产量竞争模型 Пi (qi ,qj ) = qi [p (qi+qj ) - c] = qi [a – (qi+qj ) - c] 若一对战略(si * ,sj *)是纳什均衡,则对每个参与者i,si *应满足 ui (si * ,sj *) ≥ ui (si,sj*) 上式对si中每一个可选战略si都成立。在古诺的双寡头垄断模型中,上面的 条件可具体表述为:若一对产出组合(q1*,q2 *)为纳什均衡,则对每一个 企业i,qi *应为下面最大化问题的解: * * 0 0 max ( , ) max [ ( ) ] i i i i j i i j q q q q q a q q c = − + − 设qj *<a-c,企业i最优化问题的一阶条件为: 1 * ( ) 2 q a q c i j = − −

§8-1头垄断企业的静态竞争及其博弃模型 也即是,若产量组合(q六,q*)为纳什均衡,则企业的产量选择必须满足: 9= 三(a-q2-c) a-c 92=三(a-9-℃) 反应函数(反应曲线)与纳什均衡产量。假定企业1的战略q1满足q1<a-c, 企业2的最优反应为: R(a 类似地,如果q2<a-c,则企业1的最优反应为: R(g)=2(a-9g-c 以上两式分别是企业2对企业1产量q1的反应函数和企业1对企业2产量q2的 反应函数。在这里,反应函数表示的是每个企业的最优战略(产量)是另 一个企业产量的函数。 7
7 §8-1 寡头垄断企业的静态竞争及其博弈模型 也即是,若产量组合(q1*,q2 *)为纳什均衡,则企业的产量选择必须满足: * 1 2 1 ( ) 2 q a q c = − − * 2 1 1 ( ) 2 q a q c = − − * * 1 2 3 a c q q − = = 反应函数(反应曲线)与纳什均衡产量。假定企业1的战略q1满足q1<a-c, 企业2的最优反应为: 2 1 1 1 ( ) ( ) 2 R q a q c = − − 类似地,如果q2<a-c,则企业1的最优反应为: 1 2 2 1 ( ) ( ) 2 R q a q c = − − 以上两式分别是企业2对企业1产量q1的反应函数和企业1对企业2产量q2的 反应函数。在这里,反应函数表示的是每个企业的最优战略(产量)是另 一个企业产量的函数
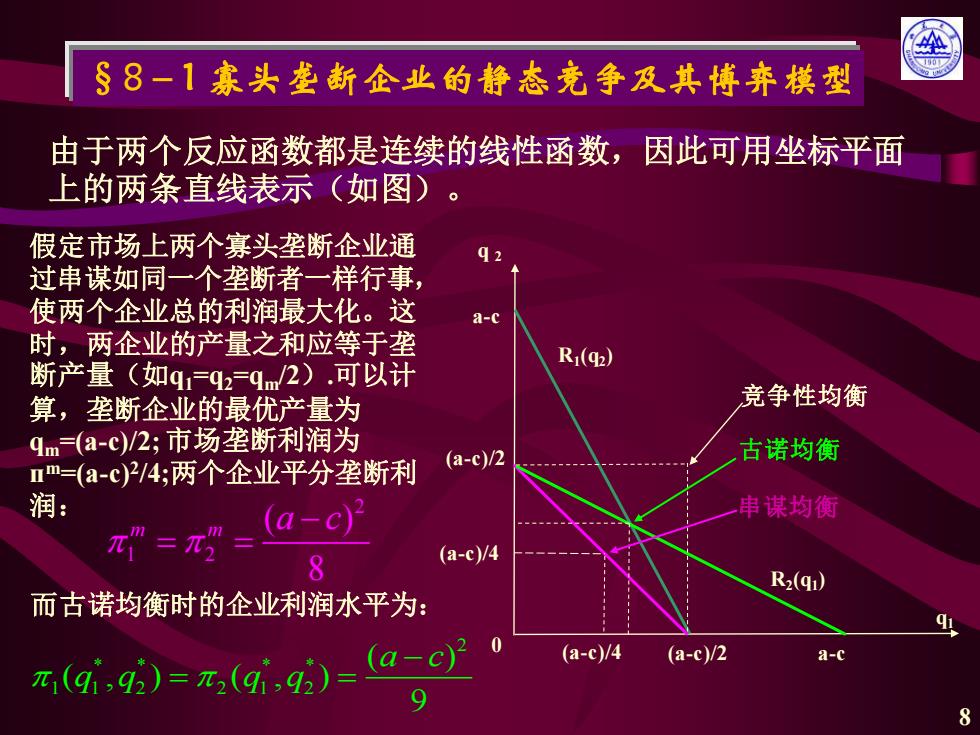
§8-1寡头垄断企业的静态竟争及其博弃模型 由于两个反应函数都是连续的线性函数,因此可用坐标平面 上的两条直线表示(如图)。 假定市场上两个寡头垄断企业通 过串谋如同一个垄断者一样行事, 使两个企业总的利润最大化。这 a-c 时,两企业的产量之和应等于垄 Ri(q2) 断产量(如q=q2=q2).可以计 算,垄断企业的最优产量为 竞争性均衡 qm=(a-c)/2;市场垄断利润为 古诺均衡 mm-(a-c)2/4;两个企业平分垄断利 (a-c)/2 润: 串谋均衡 == (a-)2 8 (a-c)/4 R2(q1) 而古诺均衡时的企业利润水平为: πq.9=石(qg=ae (a-c)/4 (a-c)/2 a-c 8
8 §8-1 寡头垄断企业的静态竞争及其博弈模型 由于两个反应函数都是连续的线性函数,因此可用坐标平面 上的两条直线表示(如图)。 q1 q 2 a-c (a-c)/2 (a-c)/4 (a-c)/4 (a-c)/2 a-c 0 竞争性均衡 古诺均衡 串谋均衡 R2 (q1 ) R1 (q2 ) 假定市场上两个寡头垄断企业通 过串谋如同一个垄断者一样行事, 使两个企业总的利润最大化。这 时,两企业的产量之和应等于垄 断产量(如q1=q2=qm/2).可以计 算,垄断企业的最优产量为 qm=(a-c)/2; 市场垄断利润为 п m=(a-c)2 /4;两个企业平分垄断利 润: 2 1 2 ( ) 8 m m a c − = = 而古诺均衡时的企业利润水平为: 2 * * * * 1 1 2 2 1 2 ( ) ( , ) ( , ) 9 a c q q q q − = =
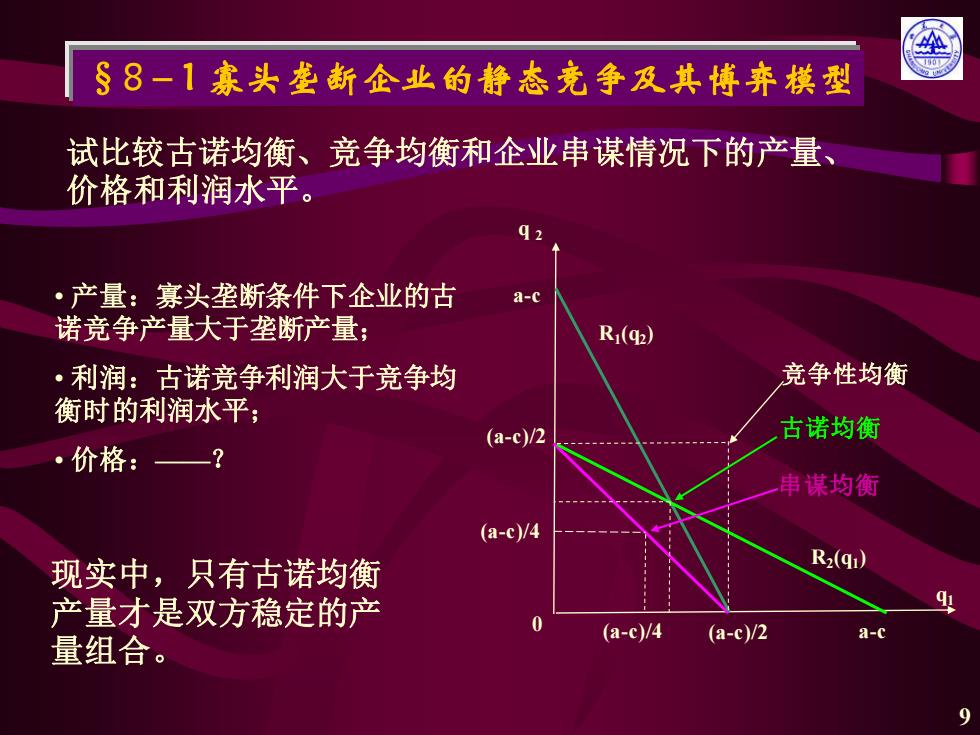
§8-1赛头垄断企业的静态竞争及其博弃模型 试比较古诺均衡、竞争均衡和企业串谋情况下的产量、 价格和利润水平。 92 ·产量:寡头垄断条件下企业的古 a-c 诺竞争产量大于垄断产量; R1(q2) ·利润:古诺竞争利润大于竞争均 竞争性均衡 衡时的利润水平; (a-c)/2 古诺均衡 ·价格:一? 串谋均衡 (a-c)/4 现实中,只有古诺均衡 R2(q) 产量才是双方稳定的产 9 量组合。 (a-c)/4 (a-c)/2 a-c 9
9 §8-1 寡头垄断企业的静态竞争及其博弈模型 q1 q 2 a-c (a-c)/2 (a-c)/4 (a-c)/4 (a-c)/2 a-c 0 竞争性均衡 古诺均衡 串谋均衡 R2 (q1 ) R1 (q2 ) 试比较古诺均衡、竞争均衡和企业串谋情况下的产量、 价格和利润水平。 • 产量:寡头垄断条件下企业的古 诺竞争产量大于垄断产量; • 利润:古诺竞争利润大于竞争均 衡时的利润水平; • 价格:——? 现实中,只有古诺均衡 产量才是双方稳定的产 量组合

§8-1寡头垄断企业的静态竞争及其博弃模型 2.多家企业的古诺竞争模型 设古诺模型中有家厂商,q为厂商的产量,Q为市场总产量,p为市场出清 价格,且已知p(Q)=a-Q。假设厂商生产q产量的总成本为C(q)=cq,也就是 说没有固定成本,且各厂商的边际成本都相同(c<a)。设各厂商同时选择 产量,则 花,=p9,-cq,三(a 其中,i=1,2,,n 将利润函数对q求导,并令导数为0,得 a元 9,-c=0 由此可以解得各厂商对其他厂商产量的反应函数为: 10
10 §8-1 寡头垄断企业的静态竞争及其博弈模型 2. 多家企业的古诺竞争模型 设古诺模型中有n家厂商,qi为厂商i的产量,Q为市场总产量,p为市场出清 价格,且已知p(Q)=a-Q。假设厂商i生产qi产量的总成本为Ci (qi )=cqi,也就是 说没有固定成本,且各厂商的边际成本都相同(c<a)。设各厂商同时选择 产量,则 ( ) n i i i i i i i j i pq cq a q q q cq = − = − − − 其中,i=1,2,…, n 将利润函数对qi求导,并令导数为0,得 2 0 n i j j i i a q q c q = − − − = 由此可以解得各厂商对其他厂商产量的反应函数为: