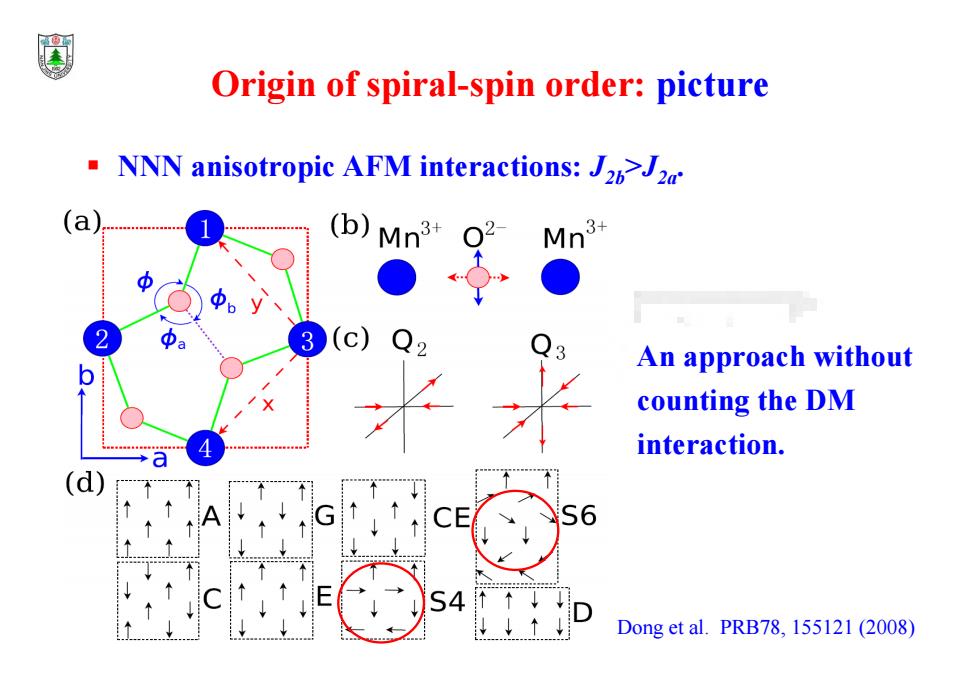
Origin of spiral-spin order:picture NNN anisotropic AFM interactions:J262 a (b)Mn3 Mn 3 2 An approach without counting the DM interaction. S6 ↓↑ Dong et al.PRB78,155121(2008)
Dong et al. PRB78, 155121 (2008) NNN anisotropic AFM interactions: J2b>J2a. An approach without counting the DM interaction. Origin of spiral-spin order: picture
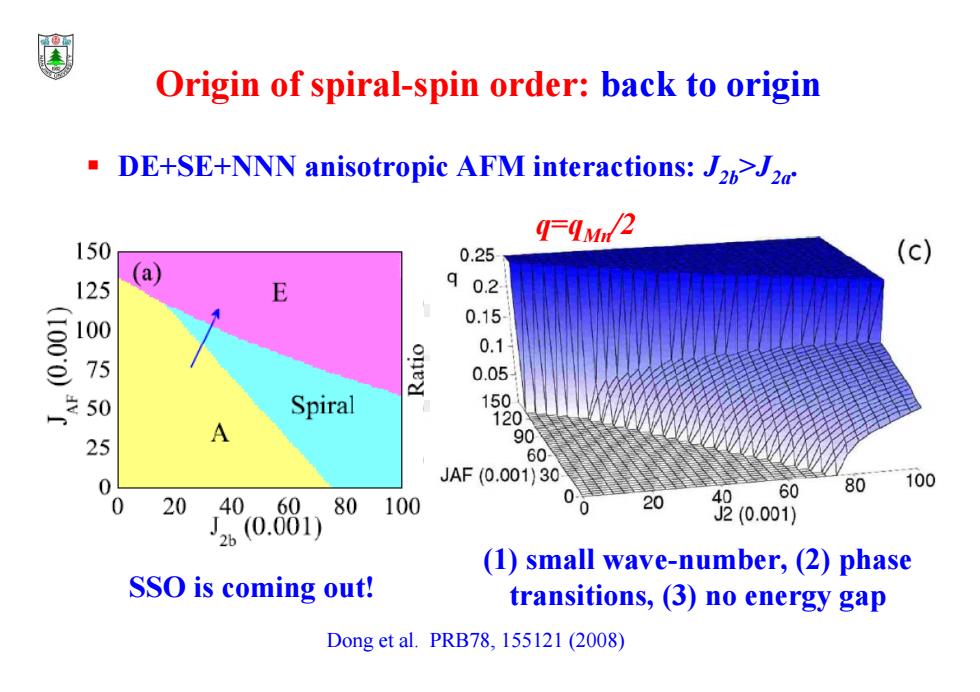
Origin of spiral-spin order:back to origin DE+SE+NNN anisotropic AFM interactions:J22 FqM2 150 0.25 (c) (a) 125 90.2 0.15 100.00 100 0.1 75 0.05 50 Spiral 15 120 25 A 0 60 JAF(0.001)30 80 100 60 0 20 4060 80 100 。 20 40 J20.001) J2(0.001) (1)small wave-number,(2)phase SSO is coming out! transitions,(3)no energy gap Dong et al.PRB78,155121(2008)
DE+SE+NNN anisotropic AFM interactions: J2b>J2a. SSO is coming out! (1) small wave-number, (2) phase transitions, (3) no energy gap q=qMn/2 Dong et al. PRB78, 155121 (2008) Origin of spiral-spin order: back to origin
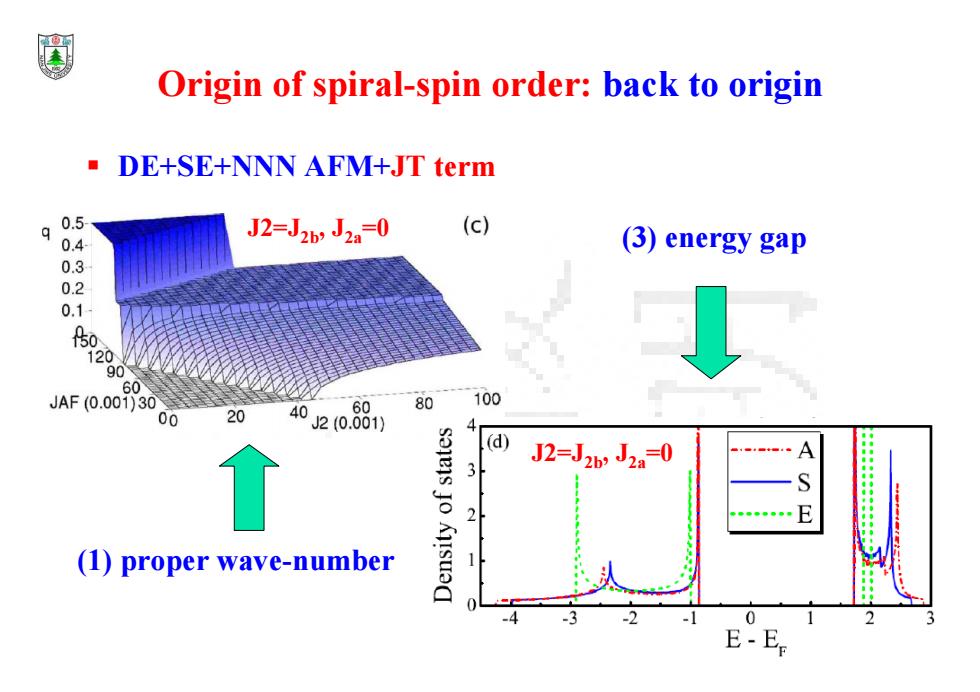
Origin of spiral-spin order:back to origin DE+SE+NNN AFM+JT term 0.5 (c) 0.4 J2=J2b2 J2=0 (3)energy gap 0.3 0.2 0.1 f5 120 JAF(0.001)30 40 60 80 100 00 20 J2(0.001) (d) J2=J26,J2a-0 A 3 2 (1)proper wave-number -3 -2 0 2 E-Er
DE+SE+NNN AFM+JT term (1) proper wave-number (3) energy gap J2=J2b, J2a=0 J2=J2b, J2a=0 Origin of spiral-spin order: back to origin
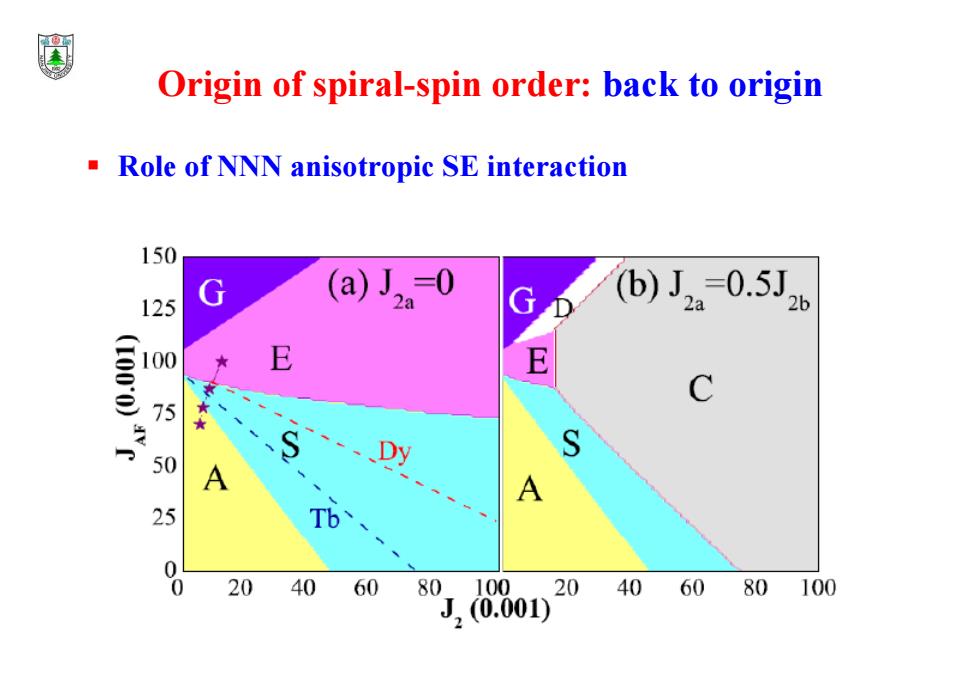
Origin of spiral-spin order:back to origin Role of NNN anisotropic SE interaction 150 (a) =0 125 G 2a )J2=0.5J2 100.00 100 75 50 A 25 Tb 0 20 40 60 80 10020 40 60 80 100 J2(0.001)
Role of NNN anisotropic SE interaction Origin of spiral-spin order: back to origin
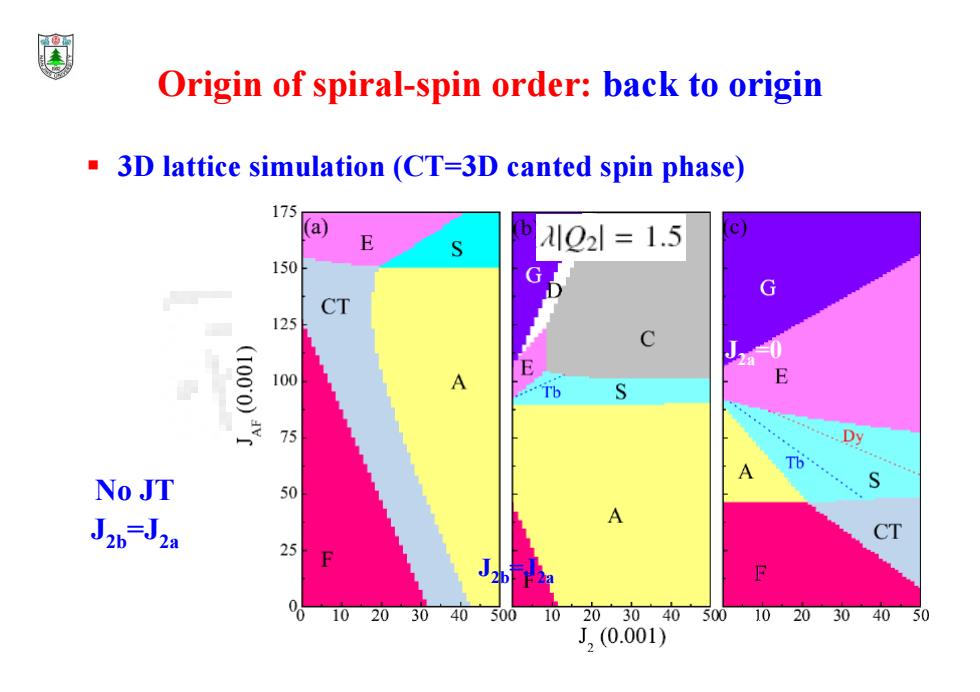
Origin of spiral-spin order:back to origin 3D lattice simulation(CT=3D canted spin phase) 175 (a) E λQ2l=1.5 150 CT 125 100.0 100 A Tb 75 D Tb No JT 50 J2-52 10 20 3040 500 10 20304050010203040 50 J,(0.001)
3D lattice simulation (CT=3D canted spin phase) No JT J2b=J2a J2b=J2a J2a=0 Origin of spiral-spin order: back to origin