华南理工大学：《现代编码理论与技术》课程教学资源（PPT课件讲稿）第十章 卷积码基础

二.卷积码--有记忆的码一有记忆编码电路 000 000 000 000 000 写成矩阵形式 883888 000 000 000 000 000 101000 001000000 011 001 000 000 000 c'=m'G。'=(00,11,00,00,,） ””中”中” -。。。一 000 000 000 000 000 。。中 000 000000000.000 --- =(000,110,001,001,000.2.) (3) m'=m+m-(8 根据线性性质c'=c+c'=(110,001,001,000,000,.) +(000,110,001,001,000,.)

二. 卷积码-----有记忆的码-----有记忆编码电路 写成矩阵形式 (000,110,001,001,000,...,...) ... ... ... ... ... ... ...... ... ... ... ... ... ... ...... 000 000 000 000 000 000 ...... 000 000 000 000 000 000 ...... 000 011 001 000 000 000 ...... 000 101 000 001 000 000 ...... 000 000 000 000 000 000 ...... 000 000 000 000 000 000 ...... ' ' ' (00 11,00,00,...,) =                       c = m G = ， （3）       = + = 1 1 0 ...... 1 1 0 ...... m'' m m' 根据线性性质 c=c+c=(110, 001,001,000,000,…) + (000,110, 001,001,000,…)

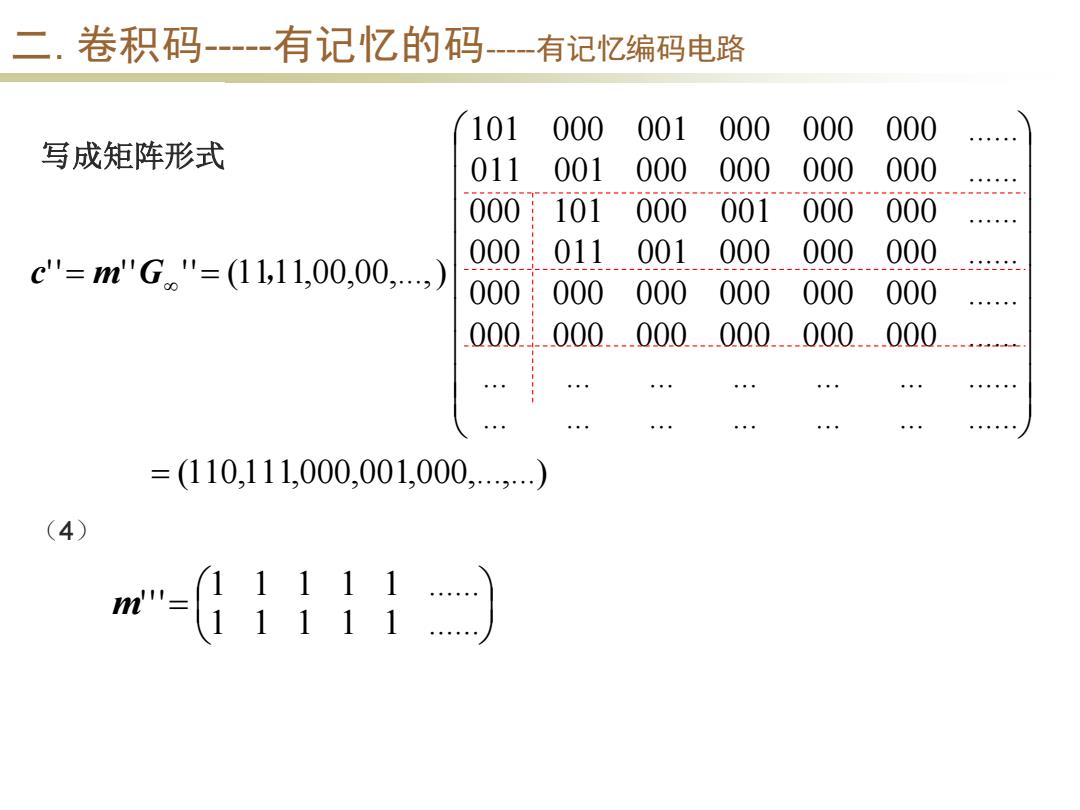
二.卷积码--有记忆的码--有记忆编码电路 101 000 001 000 000 000 写成矩阵形式 011 001 000 000 000 000 101 000 001 000 000 c"=m"G"=(11,11,00,00,,) 011 001 000 000 000 - 000 000 000 000 000 000 000 000.000 ..000..000.000 =(110,111,000,001,0002.…) (4) m-}}

二. 卷积码-----有记忆的码-----有记忆编码电路 (110,111,000,001,000,...,...) ... ... ... ... ... ... ...... ... ... ... ... ... ... ...... 000 000 000 000 000 000 ...... 000 000 000 000 000 000 ...... 000 011 001 000 000 000 ...... 000 101 000 001 000 000 ...... 011 001 000 000 000 000 ...... 101 000 001 000 000 000 ...... '' '' '' (1111,00,00,...,) =                       c = m G = ， 写成矩阵形式 （4）       = 1 1 1 1 1 ...... 1 1 1 1 1 ...... m

二.卷积码--有记忆的码 -有记忆编码电路 输入为（11,00,00,00，)的码字，记为g,从 系统分析角度，即单位脉冲序列响应。 C=mG 000 001 000 000 000 000 000 000 001 000 000 000 000 000 000 000 8 000 001 000 000 000 000 000 001 000 000 000 000 000 000 000 ” 101 000 001 000 000 000 000 =(11,11,11,11.2) 000 001 000 000 000 000 000 0 01 000 001 000 000 000 011 001 000 000 000 000 000 000 101 000 001 000 000 000 000 000 011 001 000 000 000 c=mG 可见，要从任一m求c,要找到G;要找到G,只要找到g,即输入(11,00，.)的响 应

二. 卷积码-----有记忆的码-----有记忆编码电路                           = = ... ... ... ... ... ... ... ... ... ...... 000 000 000 000 011 001 000 000 000 ...... 000 000 000 000 101 000 001 000 000 ...... 000 000 000 011 001 000 000 000 000 ...... 000 000 000 101 000 001 000 000 000 ...... 000 000 011 001 000 000 000 000 000 ...... 000 000 101 000 001 000 000 000 000 ...... 000 011 001 000 000 000 000 000 000 ...... 000 101 000 001 000 000 000 000 000 ...... 011 001 000 000 000 000 000 000 000 ...... 101 000 001 000 000 000 000 000 000 ...... (1111,11,11,...,) ''' ''' ， c m G c=mG 可见，要从任一m求c, 要找到G; 要找到G，只要找到g,即输入(11,00,…)的响 应。 输入为（11,00,00,00,..)的码字，记为g, 从 系统分析角度，即单位脉冲序列响应

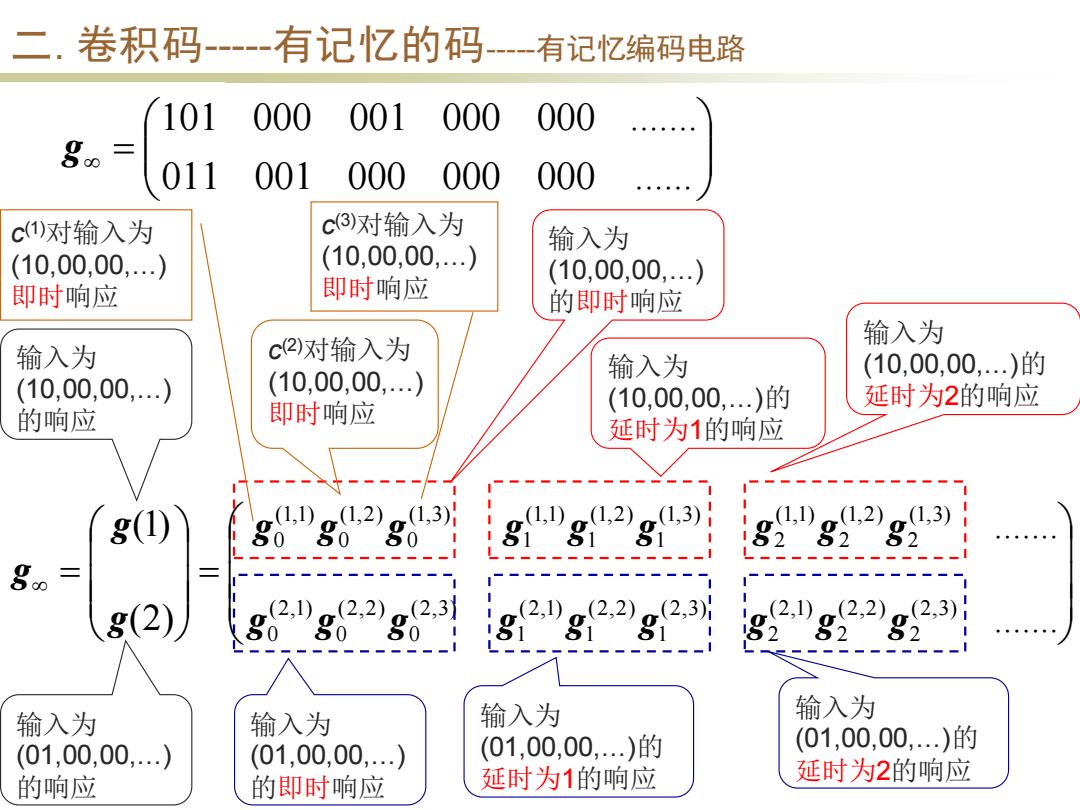
二.卷积码--有记忆的码 -一有记忆编码电路 101 000 001 000 000 .... 8= 011 001000 000 000 c)对输入为 c3)对输入为 输入为 (10,00,00.…)） (10,00,00,.)） (10,00,00,…） 即时响应 即时响应 的即时响应 输入为 输入为 c2)对输入为 输入为 (10,00,00,.)的 (10,00,00.…) (10,00,00,.) 延时为2的响应 的响应 即时响应 (10,00,00,.)的 延时为1的响应 8(1) g1,g1,2)g1,3 ,1)(1 1 (1,3) 03001 82 80= 8(2) g2 (2,2) o(2,3 (2,1) (2,3)1 (2,1) 2,3) 60 92 输入为 输入为 输入为 输入为 (01,00,00,.)的 (01,00,00,…） (01,00,00,..) (01,00,00,..)的 延时为1的响应 延时为2的响应 的响应 的即时响应

二. 卷积码-----有记忆的码-----有记忆编码电路           =            = ....... ....... (2) (1) (2,3) 2 (2,2) 2 (2,1) 2 (2,3) 1 (2,2) 1 (2,1) 1 (2,3) 0 (2,2) 0 (2,1) 0 (1,3) 2 (1,2) 2 (1,1) 2 (1,3) 1 (1,2) 1 (1,1) 1 (1,3) 0 (1,2) 0 (1,1) 0 g g g g g g g g g g g g g g g g g g g g g 输入为 (10,00,00,…) 的响应 输入为 (01,00,00,…) 的响应 输入为 (10,00,00,…) 的即时响应 输入为 (10,00,00,…)的 延时为1的响应 输入为 (10,00,00,…)的 延时为2的响应 输入为 (01,00,00,…) 的即时响应 输入为 (01,00,00,…)的 延时为1的响应 输入为 (01,00,00,…)的 延时为2的响应          = 011 001 000 000 000 ...... 101 000 001 000 000 ....... g c (1)对输入为 (10,00,00,…) 即时响应 c (2)对输入为 (10,00,00,…) 即时响应 c (3)对输入为 (10,00,00,…) 即时响应

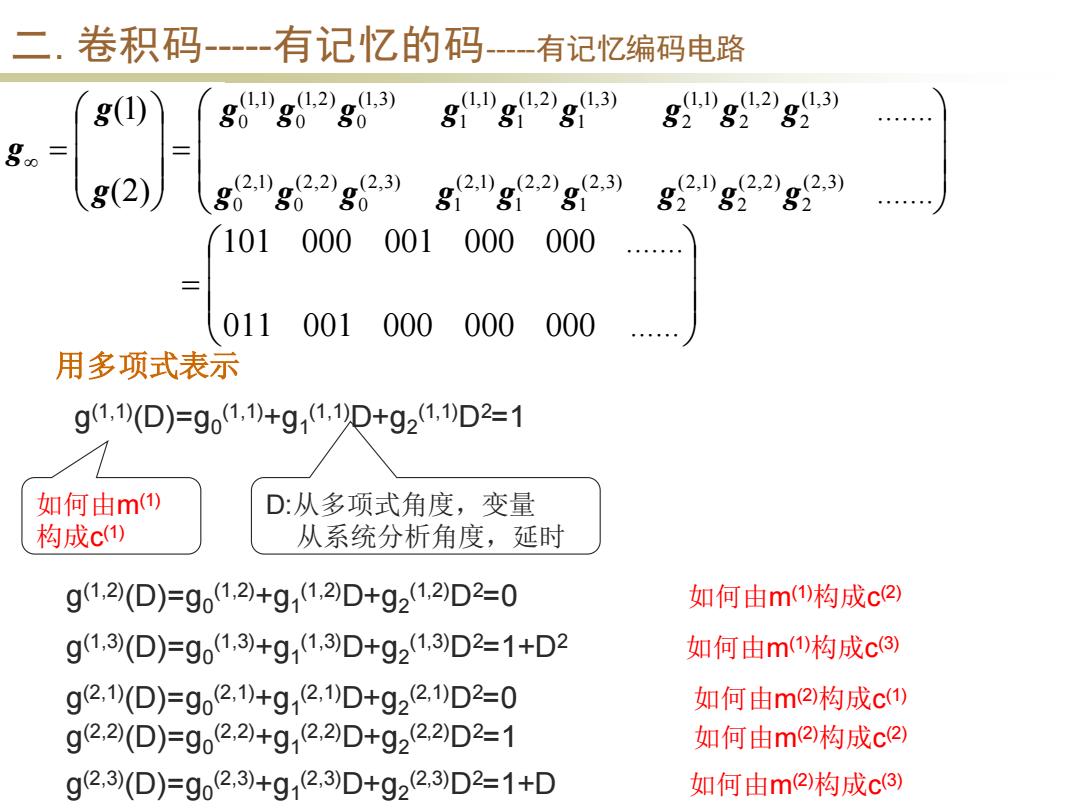
二.卷积码---有记忆的码 -有记忆编码电路 8(1) g64g02》g3 60 g4g42g43 80日 8(2) g62g62.2g623) (2,3) 6080 g2g22g2. 9(2,1)o(2,2) 101000 001000 000 011 001000000000 用多项式表示 g1,0(D)=g01,10+g11,10+g21,1)D2=1 如何由m() D:从多项式角度，变量 构成c) 从系统分析角度，延时 g1,2(D)=g01,2)+g11,2D+g21,2D2=0 如何由m()构成c2) g1,3)(D)=g01,3)+g11,3)D+g21,3)D2=1+D2 如何由m()构成c3) g2,1(D)=g02,1)+g12,1)D+g22,1)D2=0 如何由m2)构成c() g2,2(D)=g02,2+g12,2D+g22,2D2=1 如何由m②)构成c2) g2,3(D)=g02,3)+g12,3D+g22,3D2=1+D 如何由m②构成c3)

二. 卷积码-----有记忆的码-----有记忆编码电路 g (1,1)(D)=g0 (1,1)+g1 (1,1)D+g2 (1,1)D2=1 如何由m(1) 构成c (1) D:从多项式角度，变量 从系统分析角度，延时 g (1,2)(D)=g0 (1,2)+g1 (1,2)D+g2 (1,2)D2=0 如何由m(1)构成c (2) g (1,3)(D)=g0 (1,3)+g1 (1,3)D+g2 (1,3)D2=1+D2 如何由m(1)构成c (3) g (2,1)(D)=g0 (2,1)+g1 (2,1)D+g2 (2,1)D2=0 如何由m(2)构成c (1)           = 011 001 000 000 000 ...... 101 000 001 000 000 ....... 用多项式表示 g (2,2)(D)=g0 (2,2)+g1 (2,2)D+g2 (2,2)D2=1 如何由m(2)构成c (2) g (2,3)(D)=g0 (2,3)+g1 (2,3)D+g2 (2,3)D2=1+D 如何由m(2)构成c (3)           =            = ....... ....... (2) (1) (2,3) 2 (2,2) 2 (2,1) 2 (2,3) 1 (2,2) 1 (2,1) 1 (2,3) 0 (2,2) 0 (2,1) 0 (1,3) 2 (1,2) 2 (1,1) 2 (1,3) 1 (1,2) 1 (1,1) 1 (1,3) 0 (1,2) 0 (1,1) 0 g g g g g g g g g g g g g g g g g g g g g