美国阿贡国家实验室（ANL）：《电子学基础（Basic Electronics）》教学资源（讲义）Session1 Preliminary Concepts, Passive Devices

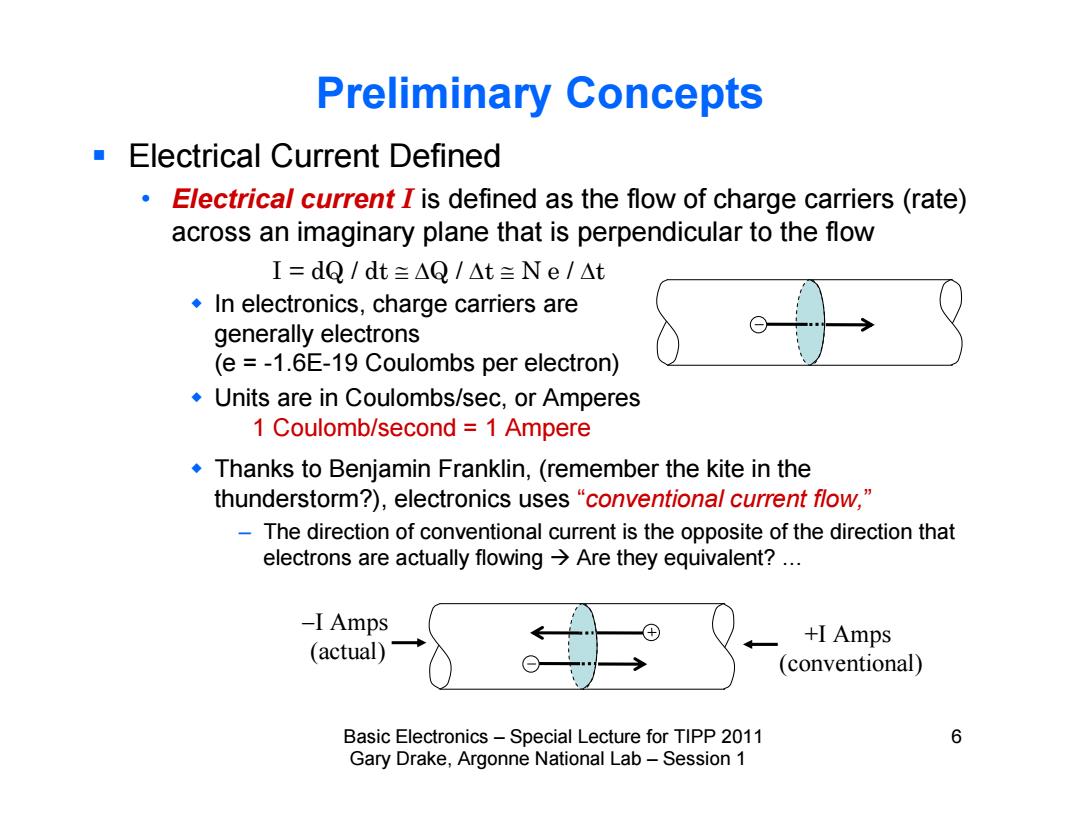
Preliminary Concepts Electrical Current Defined Electrical current I is defined as the flow of charge carriers (rate) across an imaginary plane that is perpendicular to the flow I=dQ/dt=△Q/△t三Ne/△t In electronics,charge carriers are generally electrons (e =-1.6E-19 Coulombs per electron) Units are in Coulombs/sec,or Amperes 1 Coulomb/second =1 Ampere Thanks to Benjamin Franklin,(remember the kite in the thunderstorm?),electronics uses "conventional current flow," The direction of conventional current is the opposite of the direction that electrons are actually flowing Are they equivalent?... -I Amps +I Amps (actual) (conventional) Basic Electronics-Special Lecture for TIPP 2011 6 Gary Drake,Argonne National Lab-Session 1

Basic Electronics – Special Lecture for TIPP 2011 6 Gary Drake, Argonne National Lab – Session 1 Preliminary Concepts  Electrical Current Defined • Electrical current I is defined as the flow of charge carriers (rate) across an imaginary plane that is perpendicular to the flow  In electronics, charge carriers are generally electrons (e = -1.6E-19 Coulombs per electron)  Units are in Coulombs/sec, or Amperes  Thanks to Benjamin Franklin, (remember the kite in the thunderstorm?), electronics uses “conventional current flow,” – The direction of conventional current is the opposite of the direction that electrons are actually flowing  Are they equivalent? … 1 Coulomb/second = 1 Ampere +I Amps (conventional) I Amps (actual) I = dQ / dt Q / t  N e / t

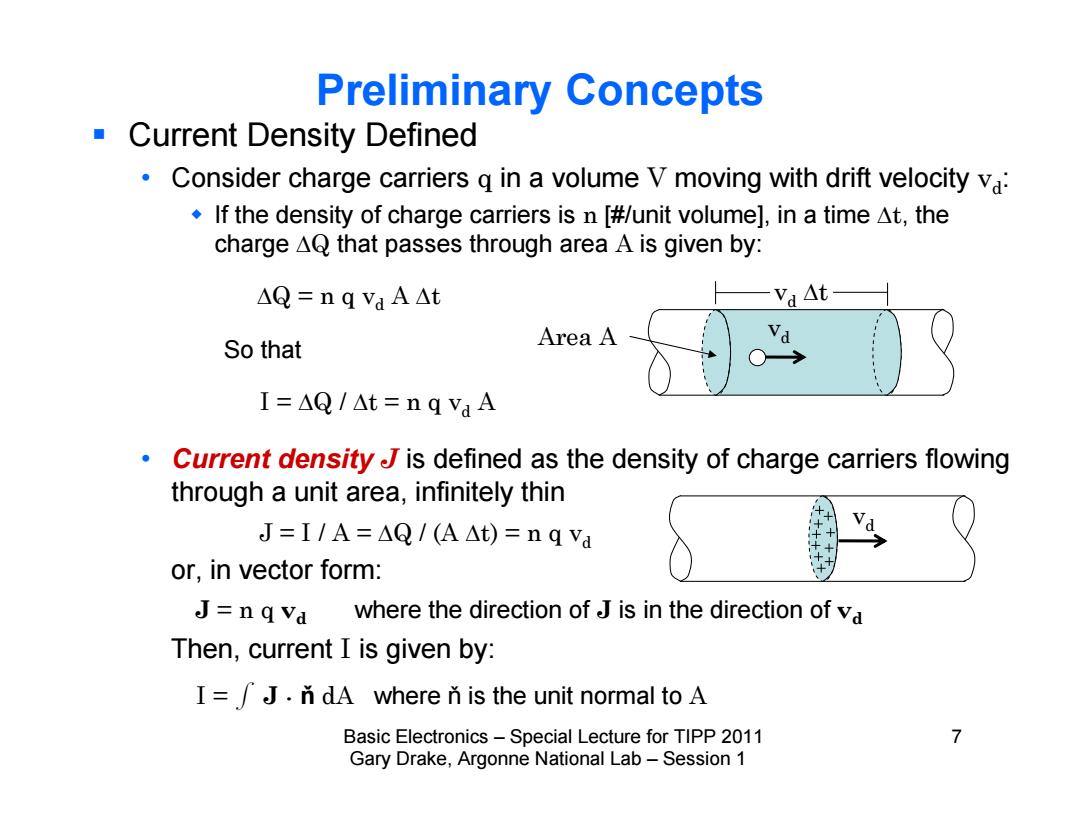
Preliminary Concepts Current Density Defined 。 Consider charge carriers g in a volume V moving with drift velocity va: .If the density of charge carriers is n [#/unit volume],in a time At,the charge AQ that passes through area A is given by: △Q=n q va A△t —vaAt So that Area A a I=△Q/At=n a va 。 Current density J is defined as the density of charge carriers flowing through a unit area,infinitely thin J=I/A=△Q/(A△t)=nqva N or,in vector form: J=n q va where the direction of J is in the direction of va Then,current I is given by: I=J.n dA where n is the unit normal to A Basic Electronics-Special Lecture for TIPP 2011 7 Gary Drake,Argonne National Lab-Session 1

Basic Electronics – Special Lecture for TIPP 2011 7 Gary Drake, Argonne National Lab – Session 1 Preliminary Concepts  Current Density Defined • Consider charge carriers q in a volume V moving with drift velocity vd:  If the density of charge carriers is n [#/unit volume], in a time t, the charge Q that passes through area A is given by: So that • Current density J is defined as the density of charge carriers flowing through a unit area, infinitely thin or, in vector form: Then, current I is given by: Q = n q vd A t I = Q / t = n q vd A vd vd t Area A J = I / A = Q / (A t) = n q vd J = n q vd where the direction of J is in the direction of vd I = f J . ň dA where ň is the unit normal to A vd

Preliminary Concepts Relationship Between J and E What determines drift velocity in a conductor,i.e.why not va =c? Answer:scattering off atoms ·For each segment,. va△t assume that charged particle starts from rest,and accelerates E to a final velocity vr F=qoE=ma→a=qoE/m vd(t)=/a dt goE tr/m The average velocity for a given path is v/2 On average,the charged particle spends a certain time accelerating in the electric field before it is captured or scattered Called the mean-free time t The mean velocity,va,it given by va=qET/(2m)>J=nqvd=nq Et/(2m) Basic Electronics-Special Lecture for TIPP 2011 8 Gary Drake,Argonne National Lab-Session 1

Basic Electronics – Special Lecture for TIPP 2011 8 Gary Drake, Argonne National Lab – Session 1 Preliminary Concepts  Relationship Between J and  • What determines drift velocity in a conductor, i.e. why not vd = c?  Answer: scattering off atoms  For each segment, assume that charged particle starts from rest, and accelerates to a final velocity vf  The average velocity for a given path is vf / 2  On average, the charged particle spends a certain time accelerating in the electric field before it is captured or scattered – Called the mean-free time   The mean velocity, vd, it given by vd = q E  / (2 m)  J = n q vd = n q E  / (2 m) vd t E F = q0 E = m a  a = q0 E / m vf(tf) = f a dt = q0 E tf / m

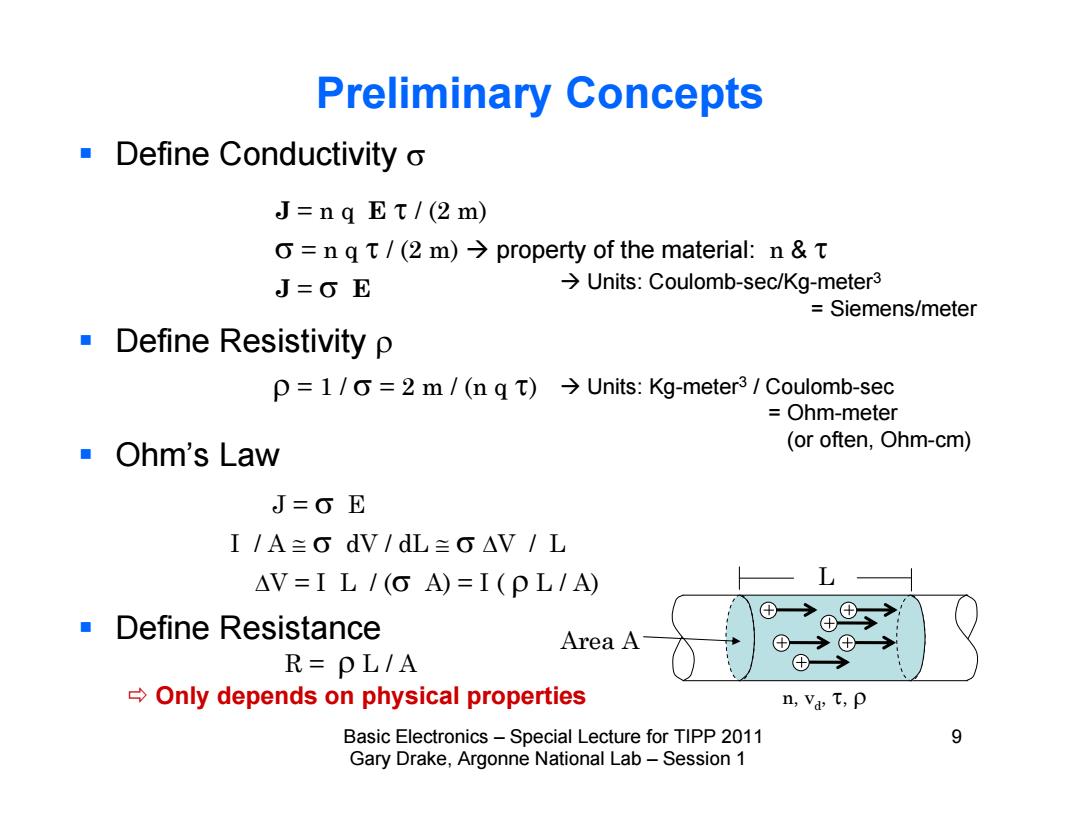
Preliminary Concepts Define Conductivity o J=nq Et/(2 m) o=ng t/(2 m)>property of the material:n t J=0E >Units:Coulomb-sec/Kg-meter3 Siemens/meter Define Resistivity p =1/0=2 m /(n q t)Units:Kg-meter3/Coulomb-sec Ohm-meter ■Ohm'sLaw (or often,Ohm-cm) J=OE I/A≥GdV/dL≥G△V/L △V=IL/(A)=I(pL/A) Define Resistance Area A ⊕→⊕→ R=PL/A ⊕→ Only depends on physical properties n,va T,p Basic Electronics-Special Lecture for TIPP 2011 9 Gary Drake,Argonne National Lab-Session 1

Basic Electronics – Special Lecture for TIPP 2011 9 Gary Drake, Argonne National Lab – Session 1 Preliminary Concepts  Define Conductivity   Define Resistivity   Ohm’s Law  Define Resistance J = n q E  / (2 m)  = n q  / (2 m)  property of the material: n &  J =  E  = 1 /  = 2 m / (n q ) J =  E I / A   dV / dL   V / L V = I L / ( A) = I (  L / A) R =  L / A n, vd, ,  L Area A  Units: Coulomb-sec/Kg-meter3 = Siemens/meter  Units: Kg-meter3 / Coulomb-sec = Ohm-meter (or often, Ohm-cm)  Only depends on physical properties

Basic Circuit Concepts Ohm's Law △V=I(pL/A) V=IR DC sources,resistive loads V(t)=I(t)R AC sources,resistive loads V(t)=I(t)Z(t) Time-dependent impedance Z(t) V(jo)=I(jo)Z(jo)-Frequency domain Define Conductance,Admittance G=1/R Conductance I=VG DC sources,resistive loads I(t)=V(t)G -AC sources,resistive loads Y(t)=1/Z(t) Admittance Y(t) I(t)=V(t)Y(t)-Time-dependent impedance I(jo)=V(j@)Y(jo)-Frequency domain Basic Electronics-Special Lecture for TIPP 2011 10 Gary Drake,Argonne National Lab-Session 1

Basic Electronics – Special Lecture for TIPP 2011 10 Gary Drake, Argonne National Lab – Session 1 Basic Circuit Concepts  Ohm’s Law  Define Conductance, Admittance V = I R - DC sources, resistive loads V(t) = I(t) R - AC sources, resistive loads V(t) = I(t) Z(t) - Time-dependent impedance Z(t) V(j) = I(j) Z(j) - Frequency domain G = 1 / R - Conductance I = V G - DC sources, resistive loads I(t) = V(t) G - AC sources, resistive loads Y(t) = 1 / Z(t) - Admittance Y(t) I(t) = V(t) Y(t) - Time-dependent impedance I(j) = V(j) Y(j) - Frequency domain V = I (  L / A)