
Basic Electronics Introductory Lecture Course for Technology and Instrumentation in Particle Physics 2011 Chicago,Illinois June9-14,2011 Presented By Gary Drake Argonne National Laboratory Session 2
Presented By Gary Drake Argonne National Laboratory Basic Electronics Introductory Lecture Course for Technology and Instrumentation in Particle Physics 2011 Chicago, Illinois June 9-14, 2011 Session 2

Session 2 Time-Varying Signals Circuits Basic Electronics-Special Lecture for TIPP 2011 2 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 2 Gary Drake, Argonne National Lab – Session 2 Session 2 Time-Varying Signals & Circuits
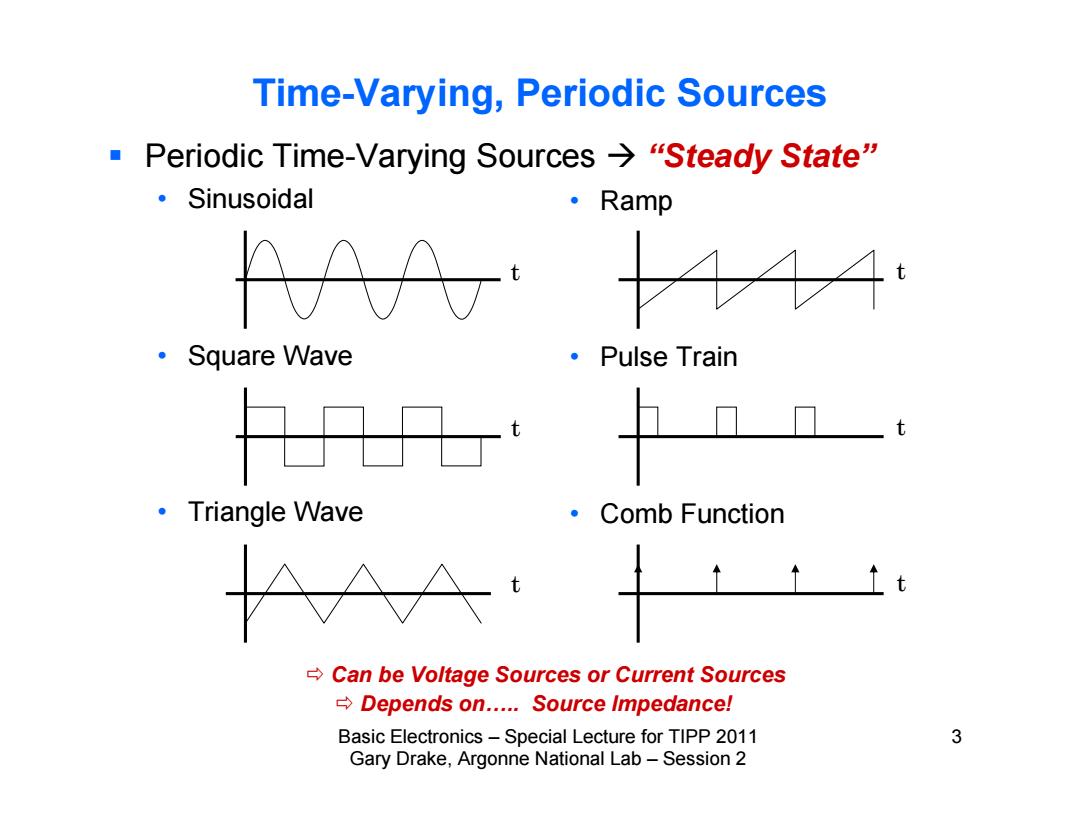
Time-Varying,Periodic Sources ·Periodic Time-Varying Sources→“Steady State” ·Sinusoidal ·Ramp ·Square Wave ·Pulse Train + 。.Triangle Wave ·Comb Function ↑t Can be Voltage Sources or Current Sources Depends on.....Source Impedance! Basic Electronics-Special Lecture for TIPP 2011 3 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 3 Gary Drake, Argonne National Lab – Session 2 Time-Varying, Periodic Sources Periodic Time-Varying Sources “Steady State” • Sinusoidal • Square Wave • Triangle Wave • Ramp • Pulse Train • Comb Function t t t t t t Can be Voltage Sources or Current Sources Depends on….. Source Impedance!

Sinusoidal Sources ■Sinusoidal Sources ·Characterized by frequency(o=2πf,phaseΦ,period T(T=l/fD, and peak amplitude Vp ∀ vo(t)=Vp sin(ot+φ) Is the average value important? VAwe=lT∫vo)dt=l/T∫Vp sin(t)dt=0→Wo,not really.. ·We often use the“Effective Value,”or RMS Vr=V1n∫o2e)dt=√1/n∫Vp2sin2otdt =Vp/V2 →This IS useful. Basic Electronics-Special Lecture for TIPP 2011 images from Wikipedia 4 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 4 Gary Drake, Argonne National Lab – Session 2 Sinusoidal Sources • Characterized by frequency f), phase , period (T = 1 / f), and peak amplitude Vp • Is the average value important? • We often use the “Effective Value,” or RMS VEFF = e 1/T f vO2(t) dt = e 1/T f VP2 sin2(t) dt = VP / S 2 Sinusoidal Sources t VAVG = 1/T f vO(t) dt = 1/T f VP sin(t) dt = 0 0 T vO(t) = VP sin(t + ) VP T -VP Images from Wikipedia 0 T 0 T No, not really… 0 T This IS useful…

Resistive Circuits with Steady State Sources Consider again a resistive network,but this time with a sinusoidal source What is the instantaneous power consumed by R? p()=V()i1() V1(t) Vp sin(@t)[Vp sin(@t)]/RI =[V,2/R]sin2(o。t) V3(t) What is the average power consumed by R? PAvG=1/TPi(t)dt v(t)=V。sin(oot) =1/T [Vp2/R]sin2(t)dt PAVG=VP2/R1 Just as before,we can use Kirchoff's Laws: VEFF2 R1,since VEPF=Vp/V2 In general, i(t)R1-V(t)=0 i(t)=V()/R1 PAVG=VEFF IEFF vo(t)=vs(t) Says that Effective Values of a sinusoid produce average power equivalent to comparable DC values Basic Electronics-Special Lecture for TIPP 2011 5 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 5 Gary Drake, Argonne National Lab – Session 2 Resistive Circuits with Steady State Sources Consider again a resistive network, but this time with a sinusoidal source vs(t) = Vp sin( t) Just as before, we can use Kirchoff’s Laws: i1(t) R1 – vs(t)= 0 i1(t) = vs(t) / R1 vO(t) = vS(t) v1(t) vs(t) What is the instantaneous power consumed by R1? p1(t) = v1(t) i1(t) = Vp sin(o t) [Vp sin(o t)] / R1 = [Vp2 / R1] sin2(o I1 t) R1 What is the average power consumed by R1? PAVG = 1/T f p1(t) dt = 1/T f [VP2/R1] sin2(o t) dt PAVG = ½ VP2 / R1 = VEFF2 / R1, since VEFF = VP / S2 In general, PAVG = VEFF IEFF 0 T 0 T Says that Effective Values of a sinusoid produce average power equivalent to comparable DC values