对率回归 以对率函数为联系函数: 1 1 y= 1+e-z 变为y= 1+e-(wTz+6) 即: wx+b “对数几率” l率(odds),反映了x作为正例的相对可能性 (log odds,亦称logit) “对数几率回归”(logistic regression) 简称“对率回归” 注意:它是 无需事先假设数据分布 分类学习算法!区 可得到“类别”的近似概率预测 可直接应用现有数值优化算法求取最优解
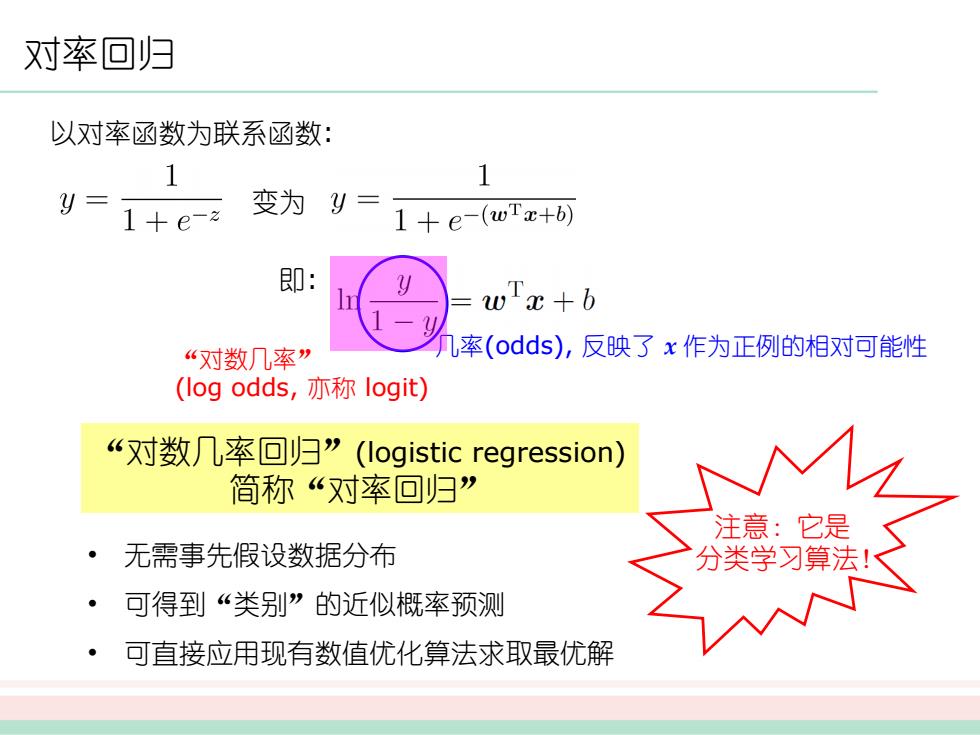
对率回归 以对率函数为联系函数: 变为 即: 几率(odds), 反映了 x 作为正例的相对可能性 “对数几率” (log odds, 亦称 logit) “对数几率回归”(logistic regression) 简称“对率回归” • 无需事先假设数据分布 • 可得到“类别”的近似概率预测 • 可直接应用现有数值优化算法求取最优解 注意:它是 分类学习算法!
线性模型做“分类” 分类 回归 △ 广义线性模型; 通过“联系函数” 如何“直接”做分类? 例如,对率回归
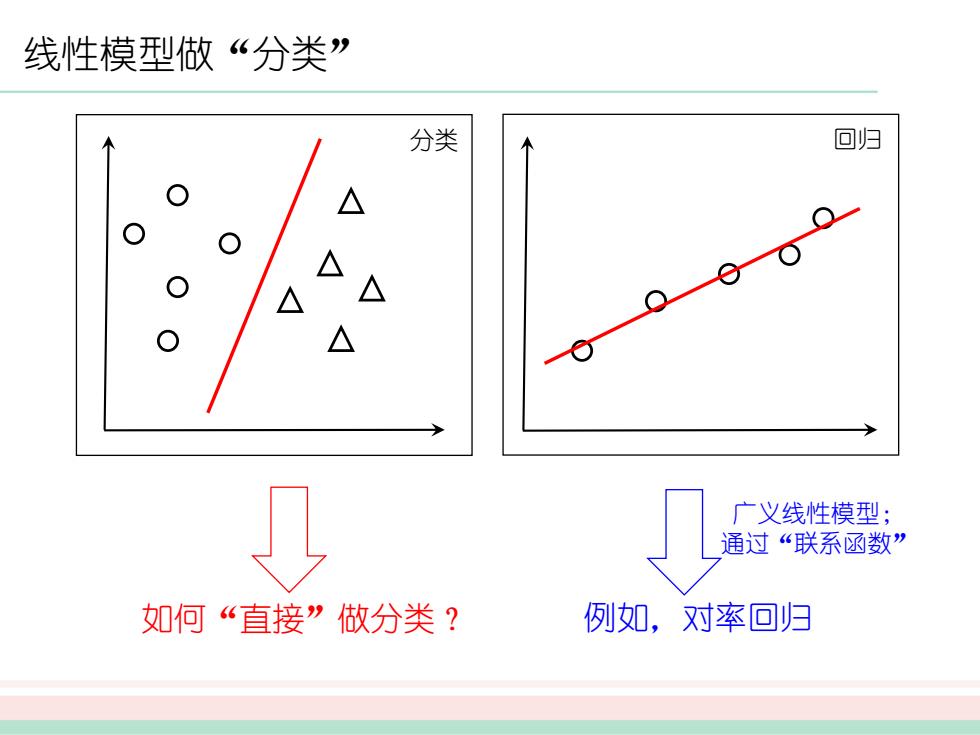
线性模型做“分类” 分类 回归 例如,对率回归 广义线性模型; 通过“联系函数” 如何“直接”做分类?

支持向量机
支持向量机
线性分类器 将训练样本分开的超平面可能有很多,哪一个更好呢? 2C1 "正中间"的:鲁棒性最好,泛化能力最强
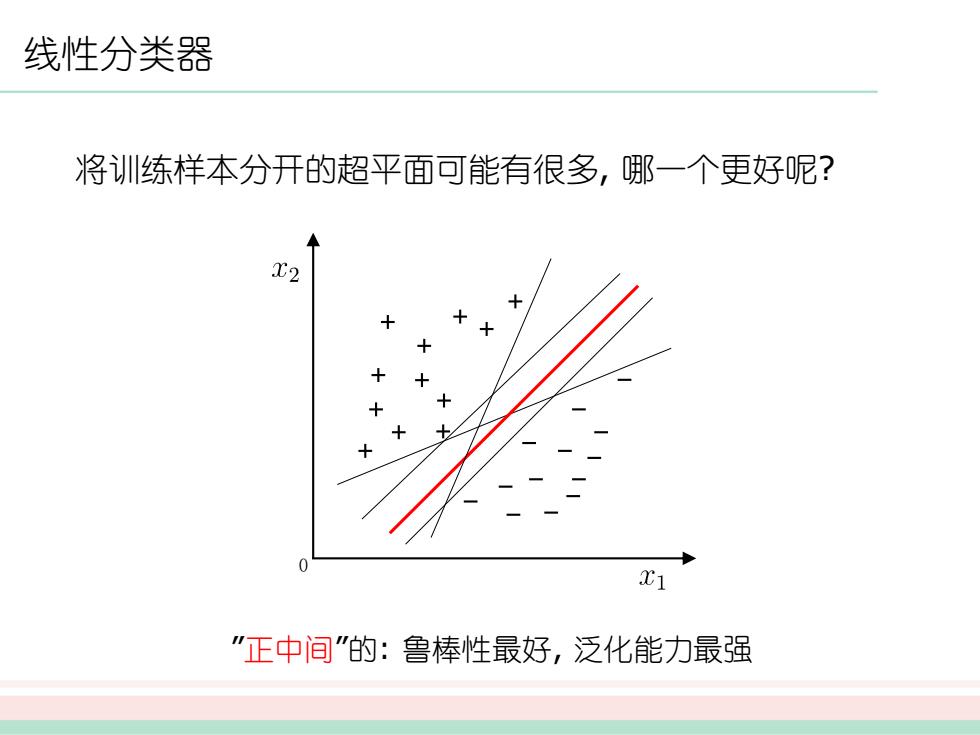
线性分类器 将训练样本分开的超平面可能有很多, 哪一个更好呢? 0 ”正中间”的: 鲁棒性最好, 泛化能力最强

间隔与支持向量 超平面方程:wc+b=0 w'x+6=1 2 w 间隔(margin) lwTx +bl wx+6=0 wll w'x+b=-1 支持向皇 (support vector)
间隔与支持向量 超平面方程: 间隔 (margin) 0 支持向量 (support vector)