
6.2单正态总体的假设检验 一、单总体均值的假设检验 iid 设X1,X。~N(μ,σ2),给定检验水平,由观测 值X1,Xn检验假设H:u=o;H:≠o心 1、σ2已知的情形-U检验 对于假设H0:u=o;H,:u≠o,构造 X-Io HoX-u 二 -N(0,1) pU≥U(号)}=a,可得拒绝域U≥U(号 查表,计算,比较大小,得出结论
6.2 单正态总体的假设检验 一、单总体均值的假设检验 值 , , 检验假设 : ; : 。 设 , , , 给定检验水平 ,由观测 1 n 0 0 1 0 2 iid 1 n x x H H X X ~ N( ), = 1、2已知的情形-U检验 0 1) 0 0 ~N( , σ n X μ σ n X μ U H 真 − − = = 对于假设H0:=0;H1:0 , 构造 查表, 计算, 比较大小, 得出结论 ) 2 ) ( 2 ( 由p{ U U } =α ,可得拒绝域:U U
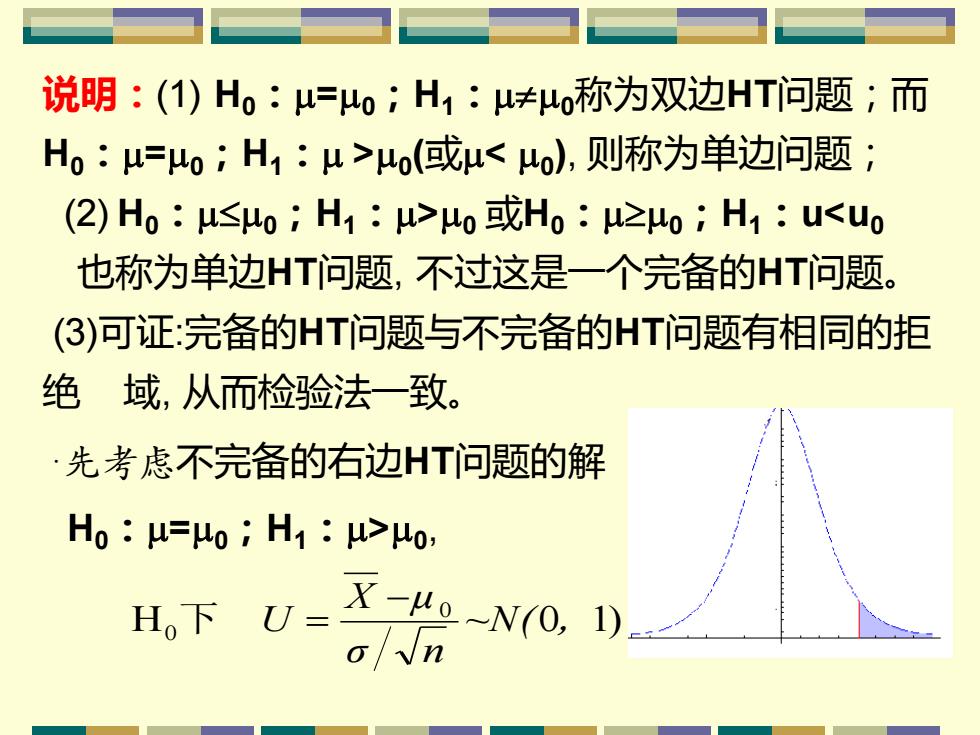
说明:(1)H0:μ=o;H1:u≠o称为双边HT问题;而 H0:u=o;H1:u>o(或μ<o,则称为单边问题; (2)Ho:μ≤o;H1:u>o或Ho:u2o;H1:u<uo 也称为单边HT问题,不过这是一个完备的HT问题。 (③)可证:完备的HT问题与不完备的HT问题有相同的拒 绝域,从而检验法一致。 ·先考虑不完备的右边HT问题的解 H0:u=o;H1:u>u0, H。下( X-uo-N0,1)
说明:(1) H0:=0;H1:0称为双边HT问题;而 H0:=0;H1: >0 (或< 0 ), 则称为单边问题; (2) H0:0;H1:>0 或H0:0;H1:u<u0 也称为单边HT问题, 不过这是一个完备的HT问题。 (3)可证:完备的HT问题与不完备的HT问题有相同的拒 绝 域, 从而检验法一致。 ·先考虑不完备的右边HT问题的解 H0:=0;H1:>0 , H 0 1) 0 0 ~N( , σ n X μ U − 下 =

pU≥U(号)}=a,可得拒绝域:W=U≥U()》 现考虑完备的右边HT问题 H0:u≤oiH1:μ>uo; H。下 X-4-N0,1) o√n 若取拒绝域为W={U≥U()}则犯第一类错误的概率为 PZ≥Ulu≤4;=PX+A-么≥U}
) { ( )} 2 ( 由p{ U U } =α ,可得拒绝域:W = U U 现考虑完备的右边HT问题 H0:0;H1:>0 , 0 0 H 0 1) − ~N( , σ n X μ 下 若取拒绝域为 W ={U U()} 则犯第一类错误的概率为 { ( )| } { ( )} 0 0 U n X P U U P − + − =

=r+ n =1-0a+%-“ ≤1-Φ(U(a)≤a 于是 supP{U≥U()l4≤4}= I≤40 故 W={U≥U()}是Ho:u≤o;H1:>o 的水平为的拒绝域
{ ( ) } 0 n U n X P − + − = − = − + n U 0 1 ( ) 1−(U()) 于是 = sup { ( )| }0 0 P U U W ={U U()} 故 是H0:0;H1:>0 , 的水平为的拒绝域

例1:设某厂生产一种灯管,其寿命X~N(u,2002),由以 往经验知平均寿命μ=1500小时,现采用新工艺后,在所 生产的灯管中抽取25只,测得平均寿命1675小时,问采用 新工艺后,灯管寿命是否有显著提高。(@=0.05) 解:H。:4=1500 H1:u>1500 H。下0=X-1500 ~N(0,1) 200/√25 由p≥U气}-a,可得拒绝域:U≥U0.05)=1645 这里 1675-1500 u =4.375>1.645 拒绝Ho 200/√25
例1:设某厂生产一种灯管, 其寿命X~ N(, 2002 ), 由以 往经验知平均寿命 =1500小时, 现采用新工艺后, 在所 生产的灯管中抽取25只, 测得平均寿命1675小时, 问采用 新工艺后, 灯管寿命是否有显著提高。(=0.05) 解: H0 : =1500 H1 : 15000 1) 200 25 1500 H 0 ~N( , X U − 下 = ) (0.05) 1.645 2 由p{ U U( } =α ,可得拒绝域:U U = 这里 4.375 1.645 200 25 1675 1500 = − u = 拒绝H0