
(6)调词公式的等价性与永真蕴含 定义:设P与Q是两个谓词公式,D是他们共同的 个体域,若对D上的任何一个解释,P与Q都有相 同的真假,则称公式P和Q在D上是等价的。记作 P→Qo ①交换率:PVQ→QVP,PAQ→QP ②结合律:(PvQ)vR<Pv(QvR) (PAQ)ARPA(QAR) ③分配律:PV(QAR)台(PVQ)A(PVR) PA(QVR)台(PAQ)V(PR) ④德.摩根律:一(PVQ)台>PA一Q (P∧Q)台→>-Pv-Q
(6)谓词公式的等价性与永真蕴含 • 定义:设P与Q是两个谓词公式,D是他们共同的 个体域,若对D上的任何一个解释,P与Q都有相 同的真假,则称公式P和Q在D上是等价的。记作 PQ。 ①交换率:PQQP,PQQP ②结合律:(PQ)RP(QR) (PQ)RP(QR) ③分配律: P(QR)(PQ)(PR) P(QR)(PQ)(PR) ④德.摩根律:(PQ)PQ (PQ)PQ

⑤双重否定律:一P台P ⑥吸收律:PV(PAQ)P PA(PvQ)台P ⑦补余律:PVP台T PA-P台F ⑧连接词化归律:P→Q<一PVQ P午Q台(P→Q)Λ(Q→P) P与Q台(PAQ)v(PA-Q) ⑨量词转换律:一(们x)P台(x)(一P) (x)P台(3x)(-P) ⑩量词分配律:(x)(PAQ)台(Vx)PA(付x)Q (臼x)(PvQ)台(臼x)Pv(臼x)Q
⑤双重否定律:PP ⑥吸收律: P(PQ)P P(PQ) P ⑦补余律: PPT PPF ⑧连接词化归律:PQPQ PQ(PQ)(QP) PQ(PQ)(PQ) ⑨量词转换律:(x)P(x)(P) (x)P(x)(P) ⑩量词分配律:(x)(PQ)(x)P(x)Q (x)(PQ)(x)P(x)Q

定义:对于调词公式P和Q,如果P→Q永真,则称P 永真蕴含Q,且称Q为P的逻辑结论,称P为Q的前提, 记作P→Q ①化简式 PAQ=→>P P∧Q=→Q ②附加式 P→PQ Q→PvQ ③析取三段论 -P,PVQ=→Q ④假言推理 P,P→Q→Q ⑤拒取式 一Q,P→Q台-P ⑥假言三段论 P+Q,Q→R→P→R ⑦二难推论 PvQ,P-R,Q→R=R ⑧全称固化 (Vx)P(x)→P(x) ⑨存在固化 (臼x)P(x)→P(x)
• 定义:对于谓词公式P和Q,如果PQ永真,则称P 永真蕴含Q,且称Q为P的逻辑结论,称P为Q的前提, 记作 PQ ①化简式 PQP PQQ ②附加式 PPQ QPQ ③析取三段论 P,PQQ ④假言推理 P,PQQ ⑤拒取式 Q,PQP ⑥假言三段论 PQ,QRPR ⑦二难推论 PQ,PR,QRR ⑧全称固化 (x)P(x)P(x) ⑨存在固化 (x)P(x)P(x)
§2.2 多值逻辑 例0<T(A)<1 T(A)为命题A的真值 在三值逻辑中:Kleene把它定义为“不能判定》 Luckasiewicz中解释为“不确定” Bochvar中解释为“无意义” 若命题的真值取0,0.5,1所得的三值逻辑为: B B A A AAB 00.51 AvB 00.51 A A 0 1 0 0 0 0 0 00.5 1 0.5 0.5 0.5 00.5 0.5 0.5 0.50.51 1 0 1 00.5 1 1 1 11
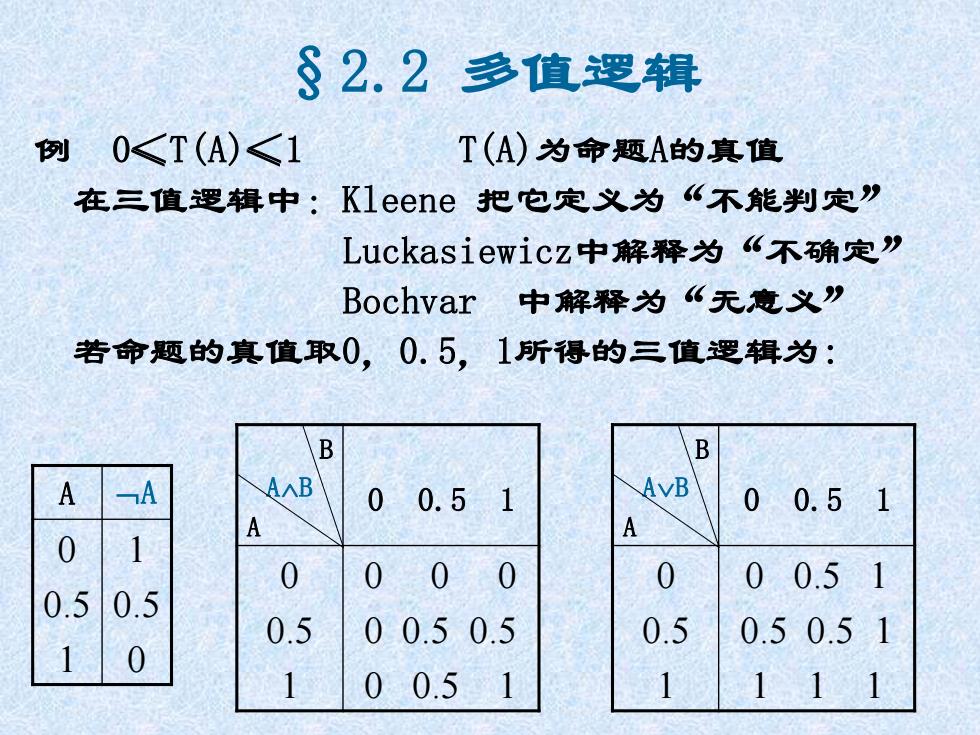
§2.2 多值逻辑 例 0≤T(A)≤1 T(A)为命题A的真值 在三值逻辑中:Kleene 把它定义为“不能判定” Luckasiewicz中解释为“不确定” Bochvar 中解释为“无意义” 若命题的真值取0,0.5,1所得的三值逻辑为: A A 0 0.5 1 1 0.5 0 B AB A 0 0.5 1 0 0.5 1 0 0 0 0 0.5 0.5 0 0.5 1 B AB A 0 0.5 1 0 0.5 1 0 0.5 1 0.5 0.5 1 1 1 1