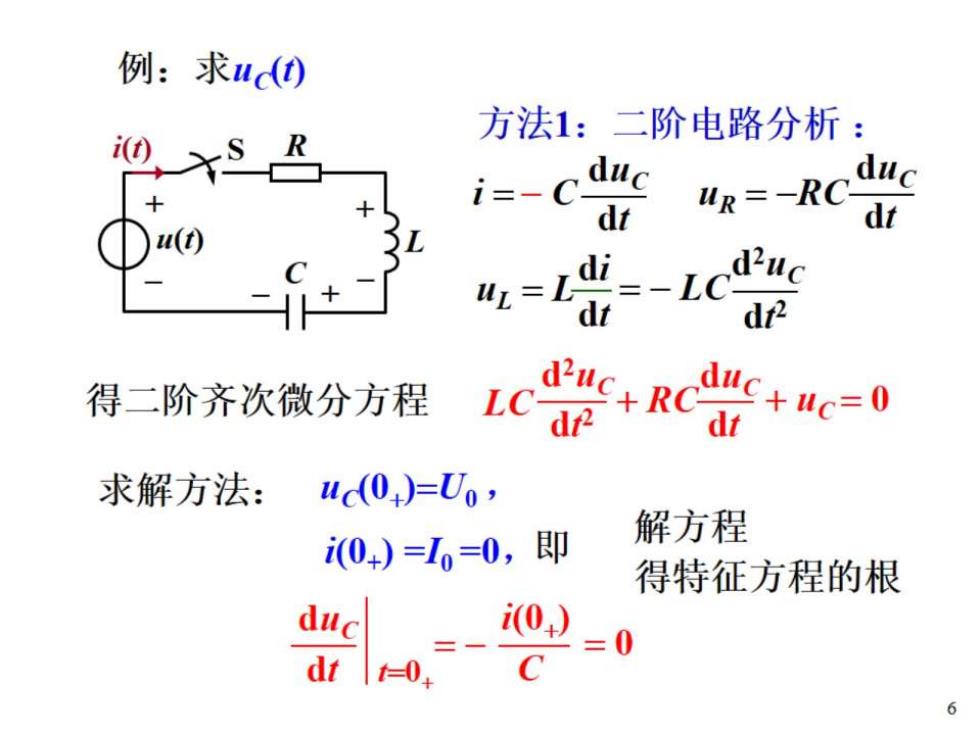
例:求u() 方法1:二阶电路分析: t i=-C. duc duc di uR=-RC di I di=-LC- 2uc dt d2 得二阶齐次微分方程 duc+RC dt LC ap duc+c=0 求解方法: ud(0)=Uo; i(04)=I=0,即 解方程 得特征方程的根 duc i0)=0 6
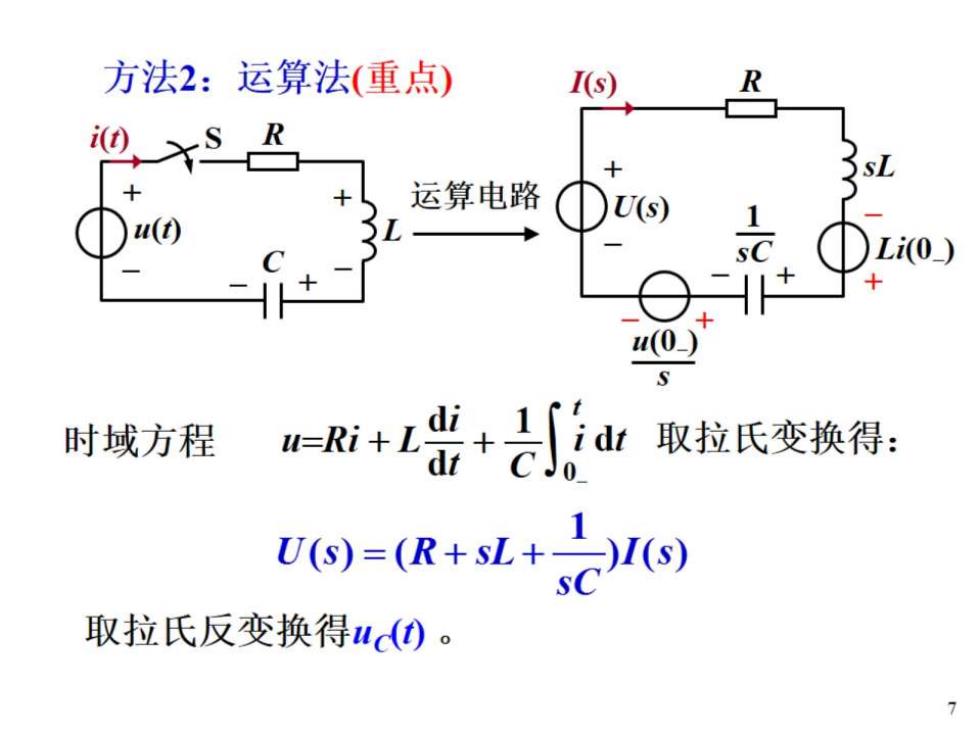
方法2:运算法(重点) I(s) i(0 运算电路 时域方程 -Ri+出+己行山取拉氏变换得: U)=(R+sL+) 取拉氏反变换得u)。 7

1.拉氏变换定义 @一个定义在[0,+o]区间的函数f),它的拉普拉 斯变换式Fs)定义为: Fw)-=cUqI与Ae-ar 式中s=叶jo为复数,被称为复频率; F(s)称为f的象函数,f)称为F(s)的原函数。 £)]表示取拉氏变换。 符号 C1[F(s)川表示取拉氏反变换。 8

2.梳理典型函数的拉氏变换(应该记住) (①单位阶跃函数0=0一ce(0} (2)单位冲激函数f)=δ(t0三£[δ()=1 (3)指数函数ft)=ew(o为实数) ce吗-a (4)正弦函数f)=sin(ot) C [sin(f)= (⑤)余弦函数f)=cos(o) C [cos(@t)]= (⑥)斜坡函数f)=t m是 常用的拉氏变换表见教材P350之表14-1

3.本章频繁使用的拉氏变换的基本性质 (1)线性性质设:C[f()]=F(S),C[f()]=F2s) 则:CA1f(0)+A2f(0]=A1F(S)+A2F2(s) 比例、叠加 (2)微分性质 若£Lf0]=Fs),则£[f'(1=sFs)-f0) 推论c[fω(=s"Fs)-s"-f0)-sr-2f'(0)-.-一fm-1(0) 该性质可将f()的微分方程化为Fs)的代数方程。 (3)积分性质 若cmI-Fw.则cf0山-=rs 10