
第二章纯质的性质 ·17 体状态均在饱和液体线上。饱和蒸气线右侧的区域是过热蒸气区;饱和液体区左侧的区域是 被压缩液体区(也叫做过冷液体区)。超临界状态是指压力和温度高于临界值的状态。 2.3液-气区 如图2-5所示,在饱和点∫和g之间的任一状态(T,),液体和蒸气均以处于平衡状态 的混合物方式存在。以,和g分别代表饱和液体和饱T 和蒸气的比体积。以m表示系统(如图2-1所示)的总 质量,5为液相质量,m。为气相质量。则对于一个以 (T,)表示的系统状态,混合物的总容积等于液体占据 =常 的容积与蒸气占据的容积之和。 m=mrUy十ngVg (2.1) 蒸气 饱和蒸气的质量与总质量之比称为混合物的干度, 用符号x表示,即 t (2.2) 77n 考惑到m=m,十mg,可以用干度的定义将式(2.1)写成 图2-5标有饱和液体和 v=Uy十x(g一) (2.3) 饱和燕气点的Tv图 因为饱和蒸气值和饱和液体值之差经常出现在计算中, 我们常用脚标fg表示这一差值,即 Ug=Ug一f (2.4) 于是,式(2.3)可写成 ℃=U:十0g (2.5) 请注意,混合物中液体的质量百分数是100(1一x),蒸气的百分数为100x。 2.4水蒸气表 我们制作了许多物质的表格,这些表格中包含热力学性质P、?和T以及在后续各章中将 要介绍的其他性质。在附录中这些性质的值是以表和图两种形式给出的。表C-1给出了以 饱和温度为函数的水的饱和性质:表C-2给出了以饱和压力为函数的水的饱和性质。这两张 表中所包含的内容是基本相同的,选择用哪个表取决于哪个表用起来方便。我们注意到,在混 合区内压力和温度是相互关联的,因此为了确定混合物的状态,如果我们已经指定了压力,那 么我还需要指定除温度以外的另一个性质。相反,如果我们已经指定了温度,那么我们还需 要指定除压力以外的另一个性质。 表C-3列出了过热水蒸气的性质。为了确定处于过热区的单一物质的状态,需要指定两 个性质。虽然任何两个性质均可被用于确定过热状态,但是通常是用压力和温度。因此,像 这样的性质是依据相互独立的P和T给出的。 表C-4列出了被压缩液体的性质。在一个给定的温度下,液体的比体积基本上与压力无 关。比如,在表C-1中温度为100℃时,压力为100kPa对应的液体比体积为 0.001044m3/g,而10MPa对应的比体积为0.001038m3/kg,比体积的减小幅度小于百分之 一。所以通常在计算时假设被压缩液体的比体积等于同温度下饱和液体的比体积。应当注意 到的是,饱和液体的比体积随温度的上升显著增加,特别是在高温时。 表C-5给出了平衡状态下的饱和固体和饱和气体的性质。注意到冰的比体积值对饱和 固体线上的压力和温度较不敏感。而且,它比饱和液体线上的最小值要大得多(约大百分之 十)。 例2.1当1kg的饱和水在(a)1kPa(b)100kPa(c)10000kPa的压力下完全汽化时,其 体积的变化是多少?

·18· 工程热力学 解博表C-2提供了所需的值。要求的量是%=a一。应注意P的单位是MP。 (a)1kPa。所以你=129,2-0.001=129.2(m2/kg) (b)100kPa=0.1MPa。所以℃a=1.594-0.001=1.693(m2/g> (c)10000kPa=10MPa。所以=0.01803-0.00145=0.01658(mkg) 注意到低压下比体积的变化较大,而临界点附近的变化较小。这一点在图2-4的P,图中也得到 了反映。 例2.21m3的封闭容积当中有4kg的水。加热至温度达到150℃。求(a)压力,(b)蒸气的 质量,(c)蒸气的体积。 幕国、利用表C-1.150℃下4kg的饱和蒸气的体积为(0.3928)(4)=1.5712m。因为给定的 容积低于这个值,我们假定其状态在湿蒸气区。 (a)湿蒸气区的压力为P=475.8kPa (b)为求蒸气的质量必须确定干度。根据式(2.3),由-1/4m3kg,可得 0.25=0.00109+x(0.3928-0.00109) 所以,x=0.2489/0.3917=0.6354。由式(2.2),蒸气的质量为 mg=x=(4)(0.6354)=2.542(g) (c)最后,蒸气的体积为 V,=tgmg=(0.3928)(2.542)=0.9985(m3) 清注意,当混合物的干度不很接近零时,其气相占有大部分的体积。在这个例子中,干度为 63.54%时气相占有了99.85%的体积。 例2.34kg的水在220kP的压力下被加热到形成气液混合物,其干度为0.8。请确定气液 混合物最终所占的体积。 。利用表C-2。为了得到220kPa的压力下的合适的数据,我们在0.2MPa和0.3MPa间做 线性插值。这样可得在220kPa的压力下 w=(38=2)0.6058-a857)+0.857=0.8297(am/g.y=a.6oi1m/g 注意到y不需要插值,因为在0.2MPa和0.3MPa两个压力下y的小数点后面四位均相同。利用 式(2.3),我们可以得到 t=y十x(-yr)=0.0011十(0.8)(0.8297-0.0011)=0.6640(m3/g) 4g所占的总体积为 V=m=(4kg)(0,6640m/kg)=2.656m3。 例2.4压力保持在540psi的恒压容器中有21b的水。加热至温度达到700℉。求该容器的 最终容积。 瓣d利用表C-3E。因为540psi正好位于该表的两个值之间,则比体积的求解就很简单 =1.3040+(0.4)(1.0727-1.3040)=1.2115(f/1bm) 最终容积为 V=m0=(2)(1.2115)=2.423(f)。 2.5理想气体状态方程 当物质的蒸气密度较低时,压力、比体积和温度可以用简单的方程相关联 Pv=RT (2.6) 其中R对于特定的气体来说是一个常数,因此被称为气体常数。这个方程就是状态方程,它 将状态参数P,和T联系了起来。所有适用于该方程的气体叫做理想气体或完美气体。请 注意,当使用理想气体方程时,压力、温度必须以绝对量表示。 气体常数R通过以下关系式同通用气体常数京相关联,对于所有气体来说F的值相同。 R=得 (2.7) 其中M是摩尔质量,其值列于表B-2,B~3。摩尔是物质的量(也就是说原子或分子的数
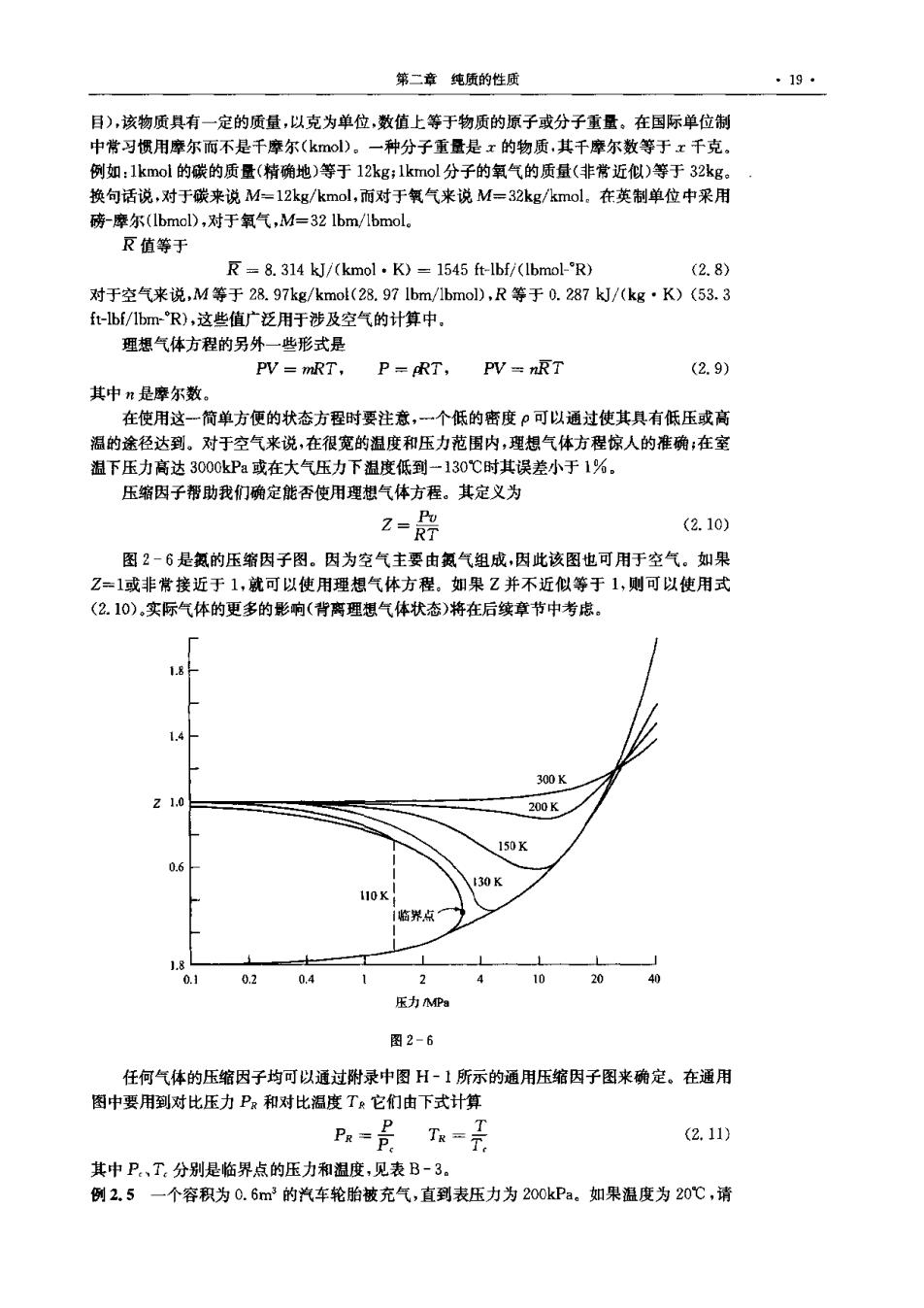
第二章纯质的性质 ·19· 目),该物质具有一定的质量,以克为单位,数值上等于物质的原子或分子重量。在国际单位制 中常习惯用摩尔而不是千摩尔(kol)。一种分子重量是x的物质,其千摩尔数等于x千克。 例如:1kmol的碳的质量(精确地)等于12kg;1kmol分子的氧气的质量(非常近似)等于32kg。 换句话说,对于碳来说M=12kg/kmol,而对于氧气来说M=32kg/kmol。在英制单位中采用 磅-摩尔(lbmol),对于氧气,M=321bm/1bmol。 反值等于 R=8.314 kJ/(kmol.K)1545 ft-lbf/(lbmol-R) (2.8) 对于空气来说,M等于28.97kg/kmo(28.971bm/1bmol),R等于0.287kJ/(kg·K)(53.3 ft-lbf/Ibm-R),这些值广泛用于涉及空气的计算中, 理想气体方程的另外一些形式是 PV mRT, P=ART,PV=nRT (2.9) 其中n是摩尔数。 在使用这-一简单方便的状态方程时要注意,一个低的密度ρ可以通过使其具有低压或高 温的途径达到。对于空气来说,在很宽的温度和压力范围内,理想气体方程惊人的准确;在室 温下压力高达3000kPa或在大气压力下温度低到一130℃时其误差小于1%。 压缩因子帮助我们确定能否使用理想气体方程。其定义为 2-是 (2.10) 图2-6是氨的压缩因子图。因为空气主要由氨气组成,因此该图也可用于空气。如果 Z=1或非常接近于1,就可以使用理想气体方程。如果Z并不近似等于1,则可以使用式 (2.10),实际气体的更多的影响(背离理想气体状态)将在后续章节中考虑。 4 300K 1.0 200K 150K 0.6 110K 1临界点 0.1 0.2 0.4 2 10 20 40 压力MPa 图2-6 任何气体的压缩因子均可以通过附录中图H-1所示的通用压缩因子图来确定。在通用 图中要用到对比压力PR和对比温度T兵它们由下式计算 R=景T=素 (2.11) 其中P、T:分别是临界点的压力和温度,见表B-3。 例2.5一个容积为0.6m3的汽车轮胎被充气,直到表压力为200kPa。如果温度为20℃,请

·20· 工程热力学 计算轮胎中空气的质量。 解销在此例的条件下,空气可被假设为理想气体。在理想气体方程PV=mRT中,我们应该使 用绝对压力和绝对温度。取P=100kPa, P=200+100=300kPa,T=20+273=293K 则可以算出质量 m-器-28品-214e 必须检查上述方程中的单位。 例2.6接近地球表面(海拔10000m以下)的大气温度,可以用T(z)=(15-0.00651z)℃近 似计算。若x=0处,P=101kPa,请计算海拔3000m处的压力。 靴意式(1.8)将压力变化与海拔高度变化关联了起来。我们可以将空气的理想气体方程写成 如下形式 P=287T-()km=29.37 因此,式(1.8)可以写成 P dP=-29.3T 利用所给的T()的方程,我们有 p dP=29.3D(288-0.06517dk 为了用开尔文表达温度,我们在式中给温度加了2?3。为了积分上式,我门必须分离变量 dp dz -(29.3)(288-0.00651 在适当的界限之间积分 了背-32a丽-(3(a)川2盖 dz 288-0.00651x h6=[5.24n(2a8-a60651w]m=-0368 得到结栗为P=(101)(ea)=69.9(kPa)。 2.6非理想气体状态方程 很多状态方程被推荐用于计算非理想气体的状态,像当压力较高(对于很多气体来说> 4MPa)或当温度接近饱和温度时气体的状态。没有一个可接受的标准能用来确定理想气体方 程能否被使用或本节中的非理想气体方程是否一定要使用。通常,在问题中会明确地表述必 须考忠非理想气体的影响,否则,就按理想气体假设求解问题。 范德瓦耳斯(van der Waals))状态方程试图考虑被气体分子占据的体积和分于之间的吸引 力。该方程为 P=RT 6导 (2.12) 其中常数a和b与表B-3中的临界点数据有关 a-,6=爱 64P。, (2.13) 这些常数还列在表B一~8中以简化计算。 一个改进的方程是瑞德里奇-邝(Redlich-Kwong)状态方程 P=RT 0-6(u+b)√T (2.14) 其中的常数为 a=0.4275R, P. 6=0.0867F℃ (2.15)

第二章纯质的性质 ·21· 以上常数同样列于表B-8中。 位力状态方程将乘积P做级数展开,最常见的展开式为 P-g+BKD+C+… (2.16) 其中我们很关心B(T),因为它表示对理想气体定律的一阶修正。对于特定的气体,必须确定 函数B(T),C(T)等。 例2.7使用(a)理想气体方程,(b)范德瓦耳斯方程,(c)瑞德里奇-邝方程,(d)压缩因子, (e)水蒸气表。计算温度为500℃,密度为24kg/m3的水蒸气的压力。 解(a)使用理想气体方程,P-pRT-(24)(0.462)(773)-850kPa,其中的气体常数查自表 B-2。 (b)采用表B-8中a和b的值,由范德瓦耳斯方程得 p=。-号-62Ka 1.703 =7950(kPa) 4-0.0169 /1 24 (c)利用查自表B-8中a和b的值,由瑞德里奇邝方程得 P=RT a (0.462)(773) 43.9 0-6 (v+6)/T =7930(kPa) 24-0.00117 (会)(分+.017)丽 ()从附录中图H-1所示的通用压缩因子图中可以查得压缩因子,为使用该曲线图,我们必须知 道对比温度和压力: =票-2=19Pk-胃-2器=062 由(a)(b)和(c)的结果可以确定上式中的预估压力值。使用压缩因子图(该图对T:和PR的精 度相当不敏思,因此容许对这两个值进行估取)和式(2.10),可得 P=RT=0.93)0,42)(77=7970(kPa) 1/24 (e)水蒸气表提供了压力的最准确的值。利用T=500℃,v=1/24=0.0417(m3/g),可以查到 P=8000kPa,由此可见利用理想气体状态方程产生了7.1%的误差,其他三种方法的误差均小于 1%。 习 题 2.1比体积为0.2m/kg,绝对压力为(a)40kPa(b)630kPa的水蒸气的干度是多少?每种 情况下的温度是多少? 解T(a)将表C-2中的数据用于式(2.3),可以计算干度如下: t=y+x(4-y),0.2=0.001+x(3.993-0.001),x=0.04985 查表C-2,由压力可查得温度:T=75.9℃。 (b)查表C-2,在0.6Ma和0.8MPa之间插值得 w=(侵)0,.2404-0.315n+03157=0304, y=0.0011 由式(2.3)得 0.2=0.0011+x(0.3044-0.0011),x=0.6558 温度经过插值得 T=(侵)170.4-158.9)+158.9=1606℃ 2.2如果千度为85%,求(a)160℃(b)221℃时水的比体积。 解谭(a)查表C-1并利用式(2.3)可得 v=4+x(-r)=0.0011+(0.85)(0.3071-0.0011)=0.2612 (b)必须插值求,和!的值。利用220℃和230℃时的数据,可得