【智能系统】基于度和聚类系数的中国航空网络重要性节点分析

第11卷第5期 智能系统学报 Vol.11 No.5 2016年10月 CAAI Transactions on Intelligent Systems 0ct.2016 D0I:10.11992/is.201601024 网络出版地址：htp:/ww.cnki.net/kcms/detail/23.1538.TP.20160824.0929.014.html 基于度和聚类系数的中国航空网络重要性节点分析 闫玲玲12，陈增强123，张青3 (1.南开大学计算机与控制工程学院，天津300350：2.南开大学智能机器人技术天津市重点实验室，天津300350： 3.中国民航大学理学院，天津300300) 摘要：运用度中心性、接近中心性、介数中心性、特征向量中心性和半局部中心性5种方法，对中国航空网络进行节 点重要性排序：对重要节点分别进行蓄意攻击和随机攻击，采用脆弱性指标验证排序方法的有效性，仿真结果表明 介数中心性能够更准确地刻画中国航空网络中节点的重要性；在航空网络的背景下，将节点的直接影响力和节点邻 居之间连接的紧密程度结合起来，提出了一种基于度和聚类系数的新指标，经中国航空网络实例验证，该指标的评 价准确性仅次于介数中心性，但是其时间复杂度比介数中心性低很多。 关键词：航空网络：节点重要性：度：聚类系数：复杂网络 中图分类号：N94文献标志码：A文章编号：1673-4785(2016)05-0586-08 中文引用格式：闫玲玲，陈增强，张青.基于度和聚类系数的中国航空网络重要性节点分析[J].智能系统学报，2016,11(5)：586 593. 英文引用格式：YAN Lingling,CHEN Zengqiang,ZHANG Qing.Analysis of Key Nodes in China's Aviation Network Based on the Degree Centrality Indicator and Clustering Coefficient[J].CAAI transactions on intelligent systems,2016,11(5):586-593. Analysis of key nodes in China's aviation network based on the degree centrality indicator and clustering coefficient YAN Lingling'2,CHEN Zengqiang'2.3,ZHANG Qing (1.College of Computer and Control Engineering,Nankai University,Tianjin 300350,China;2.Key Laboratory of Intelligent Robot- ics of Tianjin,Nankai University,Tianjin 300350,China;3.College of Science,Civil Aviation University of China,Tianjin 300300, China) Abstract:This paper determines the key nodes of China's aviation network based on degree centrality,closeness centrality,'betweenness'centrality,eigenvector centrality,semi-local centrality indicators,and then ranks these nodes in descending order of importance.Using a vulnerability index and reviewing risks from deliberate and ran- dom attack the effectiveness of the sorting methods is then evaluated.It is apparent from the corresponding vulnera- bility indices that the aviation network of China is most vulnerable to targeted attacks according to the betweenness centrality indicator.Moreover,based on the aviation network,this paper proposes a new evaluation method,which takes into account not only the number of neighbors,but also the clustering coefficient.Focusing on China's avia- tion network,the experimental results demonstrate that the evaluation accuracy of the new index ranks only second to the betweenness centrality,and is more efficient compared with betweenness centrality as regards time complexity. Keywords:aviation network;key nodes;degree;clustering coefficient;complex network 自20世纪初飞机问世以来，航空运输系统飞速 效、灵活的优势，尤其是在长距离运输和国际客运方 发展。与其他运输方式相比，航空运输具有及时、高 面的重要作用日益凸显[口。航空运输系统是一个 易受环境影响的开放的复杂系统，随着系统规模的 收稿日期：2016-01-15.网络出版日期：2016-08-24. 不断扩大，它在带给人们便利的同时也带来了一系 基金项目：国家自然科学基金项目(61573199)：天津自然科学基金项目 列的问题。航班延误已经成为人们司空见惯的现 (14 JCYBJC18700). 通信作者：闫玲玲.E-mail:yanlingling(@mail.nankai.eu.cm 象，于是，在自然灾害或人为因素导致航班不能正常

第 １１ 卷第 ５ 期 智 能 系 统 学 报 Ｖｏｌ．１１ №．５ ２０１６ 年 １０ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｏｃｔ． ２０１６ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６０１０２４ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ＴＰ．２０１６０８２４．０９２９．０１４．ｈｔｍｌ 基于度和聚类系数的中国航空网络重要性节点分析 闫玲玲１，２ ，陈增强１，２，３ ，张青３ （１．南开大学 计算机与控制工程学院，天津 ３００３５０； ２．南开大学 智能机器人技术天津市重点实验室，天津 ３００３５０； ３．中国民航大学 理学院， 天津 ３００３００） 摘 要：运用度中心性、接近中心性、介数中心性、特征向量中心性和半局部中心性 ５ 种方法，对中国航空网络进行节 点重要性排序；对重要节点分别进行蓄意攻击和随机攻击，采用脆弱性指标验证排序方法的有效性，仿真结果表明 介数中心性能够更准确地刻画中国航空网络中节点的重要性；在航空网络的背景下，将节点的直接影响力和节点邻 居之间连接的紧密程度结合起来，提出了一种基于度和聚类系数的新指标，经中国航空网络实例验证，该指标的评 价准确性仅次于介数中心性，但是其时间复杂度比介数中心性低很多。 关键词：航空网络；节点重要性；度；聚类系数；复杂网络 中图分类号：Ｎ９４ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１６）０５⁃０５８６⁃０８ 中文引用格式：闫玲玲，陈增强，张青．基于度和聚类系数的中国航空网络重要性节点分析［ Ｊ］． 智能系统学报， ２０１６， １１（５）： ５８６⁃ ５９３． 英文引用格式：ＹＡＮ Ｌｉｎｇｌｉｎｇ，ＣＨＥＮ Ｚｅｎｇｑｉａｎｇ，ＺＨＡＮＧ Ｑｉｎｇ．Ａｎａｌｙｓｉｓ ｏｆ Ｋｅｙ Ｎｏｄｅｓ ｉｎ Ｃｈｉｎａ􀆳ｓ Ａｖｉａｔｉｏｎ Ｎｅｔｗｏｒｋ Ｂａｓｅｄ ｏｎ ｔｈｅ Ｄｅｇｒｅｅ Ｃｅｎｔｒａｌｉｔｙ Ｉｎｄｉｃａｔｏｒ ａｎｄ Ｃｌｕｓｔｅｒｉｎｇ Ｃｏｅｆｆｉｃｉｅｎｔ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１６，１１（５）： ５８６⁃５９３． Ａｎａｌｙｓｉｓ ｏｆ ｋｅｙ ｎｏｄｅｓ ｉｎ Ｃｈｉｎａ􀆳ｓ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ ｂａｓｅｄ ｏｎ ｔｈｅ ｄｅｇｒｅｅ ｃｅｎｔｒａｌｉｔｙ ｉｎｄｉｃａｔｏｒ ａｎｄ ｃｌｕｓｔｅｒｉｎｇ ｃｏｅｆｆｉｃｉｅｎｔ ＹＡＮ Ｌｉｎｇｌｉｎｇ １，２ ， ＣＨＥＮ Ｚｅｎｇｑｉａｎｇ １，２，３ ， ＺＨＡＮＧ Ｑｉｎｇ ３ （１． Ｃｏｌｌｅｇｅ ｏｆ Ｃｏｍｐｕｔｅｒ ａｎｄ Ｃｏｎｔｒｏｌ Ｅｎｇｉｎｅｅｒｉｎｇ， Ｎａｎｋａｉ Ｕｎｉｖｅｒｓｉｔｙ， Ｔｉａｎｊｉｎ ３００３５０， Ｃｈｉｎａ； ２． Ｋｅｙ Ｌａｂｏｒａｔｏｒｙ ｏｆ Ｉｎｔｅｌｌｉｇｅｎｔ Ｒｏｂｏｔ⁃ ｉｃｓ ｏｆ Ｔｉａｎｊｉｎ， Ｎａｎｋａｉ Ｕｎｉｖｅｒｓｉｔｙ， Ｔｉａｎｊｉｎ ３００３５０， Ｃｈｉｎａ； ３． Ｃｏｌｌｅｇｅ ｏｆ Ｓｃｉｅｎｃｅ， Ｃｉｖｉｌ Ａｖｉａｔｉｏｎ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｃｈｉｎａ， Ｔｉａｎｊｉｎ ３００３００， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｔｈｉｓ ｐａｐｅｒ ｄｅｔｅｒｍｉｎｅｓ ｔｈｅ ｋｅｙ ｎｏｄｅｓ ｏｆ Ｃｈｉｎａ’ ｓ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ ｂａｓｅｄ ｏｎ ｄｅｇｒｅｅ ｃｅｎｔｒａｌｉｔｙ， ｃｌｏｓｅｎｅｓｓ ｃｅｎｔｒａｌｉｔｙ， ‘ｂｅｔｗｅｅｎｎｅｓｓ’ ｃｅｎｔｒａｌｉｔｙ， ｅｉｇｅｎｖｅｃｔｏｒ ｃｅｎｔｒａｌｉｔｙ， ｓｅｍｉ⁃ｌｏｃａｌ ｃｅｎｔｒａｌｉｔｙ ｉｎｄｉｃａｔｏｒｓ， ａｎｄ ｔｈｅｎ ｒａｎｋｓ ｔｈｅｓｅ ｎｏｄｅｓ ｉｎ ｄｅｓｃｅｎｄｉｎｇ ｏｒｄｅｒ ｏｆ ｉｍｐｏｒｔａｎｃｅ． Ｕｓｉｎｇ ａ ｖｕｌｎｅｒａｂｉｌｉｔｙ ｉｎｄｅｘ ａｎｄ ｒｅｖｉｅｗｉｎｇ ｒｉｓｋｓ ｆｒｏｍ ｄｅｌｉｂｅｒａｔｅ ａｎｄ ｒａｎ⁃ ｄｏｍ ａｔｔａｃｋ ｔｈｅ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ｔｈｅ ｓｏｒｔｉｎｇ ｍｅｔｈｏｄｓ ｉｓ ｔｈｅｎ ｅｖａｌｕａｔｅｄ． Ｉｔ ｉｓ ａｐｐａｒｅｎｔ ｆｒｏｍ ｔｈｅ ｃｏｒｒｅｓｐｏｎｄｉｎｇ ｖｕｌｎｅｒａ⁃ ｂｉｌｉｔｙ ｉｎｄｉｃｅｓ ｔｈａｔ ｔｈｅ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ ｏｆ Ｃｈｉｎａ ｉｓ ｍｏｓｔ ｖｕｌｎｅｒａｂｌｅ ｔｏ ｔａｒｇｅｔｅｄ ａｔｔａｃｋｓ ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｂｅｔｗｅｅｎｎｅｓｓ ｃｅｎｔｒａｌｉｔｙ ｉｎｄｉｃａｔｏｒ． Ｍｏｒｅｏｖｅｒ， ｂａｓｅｄ ｏｎ ｔｈｅ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ， ｔｈｉｓ ｐａｐｅｒ ｐｒｏｐｏｓｅｓ ａ ｎｅｗ ｅｖａｌｕａｔｉｏｎ ｍｅｔｈｏｄ， ｗｈｉｃｈ ｔａｋｅｓ ｉｎｔｏ ａｃｃｏｕｎｔ ｎｏｔ ｏｎｌｙ ｔｈｅ ｎｕｍｂｅｒ ｏｆ ｎｅｉｇｈｂｏｒｓ， ｂｕｔ ａｌｓｏ ｔｈｅ ｃｌｕｓｔｅｒｉｎｇ ｃｏｅｆｆｉｃｉｅｎｔ． Ｆｏｃｕｓｉｎｇ ｏｎ Ｃｈｉｎａ’ｓ ａｖｉａ⁃ ｔｉｏｎ ｎｅｔｗｏｒｋ， ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｄｅｍｏｎｓｔｒａｔｅ ｔｈａｔ ｔｈｅ ｅｖａｌｕａｔｉｏｎ ａｃｃｕｒａｃｙ ｏｆ ｔｈｅ ｎｅｗ ｉｎｄｅｘ ｒａｎｋｓ ｏｎｌｙ ｓｅｃｏｎｄ ｔｏ ｔｈｅ ｂｅｔｗｅｅｎｎｅｓｓ ｃｅｎｔｒａｌｉｔｙ， ａｎｄ ｉｓ ｍｏｒｅ ｅｆｆｉｃｉｅｎｔ ｃｏｍｐａｒｅｄ ｗｉｔｈ ｂｅｔｗｅｅｎｎｅｓｓ ｃｅｎｔｒａｌｉｔｙ ａｓ ｒｅｇａｒｄｓ ｔｉｍｅ ｃｏｍｐｌｅｘｉｔｙ． Ｋｅｙｗｏｒｄｓ：ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ； ｋｅｙ ｎｏｄｅｓ； ｄｅｇｒｅｅ； ｃｌｕｓｔｅｒｉｎｇ ｃｏｅｆｆｉｃｉｅｎｔ； ｃｏｍｐｌｅｘ ｎｅｔｗｏｒｋ 收稿日期：２０１６⁃０１⁃１５． 网络出版日期：２０１６⁃０８⁃２４． 基金项目：国家自然科学基金项目（６１５７３１９９）；天津自然科学基金项目 （１４ＪＣＹＢＪＣ１８７００）． 通信作者：闫玲玲． Ｅ⁃ｍａｉｌ：ｙａｎｌｉｎｇｌｉｎｇ＠ ｍａｉｌ．ｎａｎｋａｉ．ｅｄｕ．ｃｎ． 自 ２０ 世纪初飞机问世以来，航空运输系统飞速 发展。 与其他运输方式相比，航空运输具有及时、高 效、灵活的优势，尤其是在长距离运输和国际客运方 面的重要作用日益凸显［１］ 。 航空运输系统是一个 易受环境影响的开放的复杂系统，随着系统规模的 不断扩大，它在带给人们便利的同时也带来了一系 列的问题。 航班延误已经成为人们司空见惯的现 象，于是，在自然灾害或人为因素导致航班不能正常

第5期 闫玲玲，等：基于度和聚类系数的中国航空网络重要性节点分析 ·587· 起降的突发情况下，航空运输系统能够保持其鲁棒 2E C(i)= 性，成为人们越来越关注的问题。 k(k:-1) 刘宏鲲等)研究表明，中国城市航空网络具有 式中：E是节点，的k:个邻节点之间实际存在的边 较大的聚类系数和较短的平均路径长度，其度分布 数，即节点：的k:个邻节点之间实际存在的邻居对 服从双段幂律分布，是一个具有小世界网络特性的 的数目。聚类系数表征在网络中某一节点的两个相 无标度网络：姚红光等[)通过仿真实验得出，中国 邻节点也相邻的概率，反映的是网络的集聚化程度。 航空网络在面对随机干扰时鲁棒性较强，而在蓄意 2无向网络节点重要性指标 攻击下鲁棒性较差：不同的城市节点对于网络鲁棒 性的贡献程度不同，目前有40余个核心城市在中国 在复杂网络领域里评价节点重要性的方法有很 航空网络中占有举足轻重的地位。 多，本质上都是源于图论和基于图的数据挖掘，主要 航空网络中，准确地评估和度量节点的重要性 分为以下3类：社会网络分析、系统科学分析、信息 在提高网络的可靠性与抗毁性方面扮演着非常重要 搜索领域分析)。其本质上都是源于图论以及基 的角色。在由城市节点和通航城市间的直飞航线所 于图的数据挖掘，主要从网络拓扑结构入手进行 构成的航空网络中，如果受突发事件的影响，某城 分析。 市节点陷入瘫痪，那么这就意味着同时取消了与该 社会网络分析方法起始于20世纪40年代末， 城市节点相连的所有的航线，从而有可能引发网络 在评价节点重要性的研究领域中是比较常见的。它 中其他通航城市之间的一些运输路径中断[4)。例 主要基于这样一种假设：“重要性等价于显著性”， 如，2015年7月11日，超强台风“灿鸿”逼近上海， 即节点的重要性等价于该节点与其他节点的连接而 受台风“灿鸿”影响，上海机场终端区的通行能力下 使其具有的显著性[6)。该方法主要以网络的拓扑 降50%左右，共计取消航班300多个架次。因此，准 结构为切入点，在不破坏网络连通性的前提下对重 确评估航空网络中的重要节点，并针对其可能发生 要节点进行研究，并且通常不考虑节点集的重要 的突发状况提前制定完备的候选方案和补救措施， 性[)。通过分析网络中的某种有用信息来区分不 可以有效避免网络因受到外界干扰而造成航班大面 同节点的重要性差异，其主要的分析指标包括节点 积延误，从而保证航空运输安全高效地运营。 的度(degree)、接近度(closeness)、介数(between- ness)、特征向量(eigenvector)等。 1理论基础 2.1度中心性 将航空网络抽象为一个由点集V=[12…n] 度中心性(degree centrality)[s),就是按照度值 和边集E=[e1e2…em]组成的无向图G=[VE],顶 的大小对节点进行排列。它是网络中刻画节点重要 点数记为N=1VI,边数记为M=IE1。图的邻接矩 性最简单而又非常重要的指标。具有相同度值的节 阵记为Axn=(a),当且仅当节点：与之间有连 点在不同规模的网络中的重要程度是不同的，因此 边时ag=1,否则ag=0。 为了便于比较，将节点的度中心性进行归一化处理： 定义1无向网络中节点，的度k,是指与节点 k: 直接相连的边的数目。它与节点的重要程度有很大 upe(i)=N-1 的关系。一般而言，k的值越大，节点就越重要。其 显然，度中心性描述的是节点对于其邻居节点 表达形式为 的直接影响力，它认为一个节点的度值越大，与之有 直接联系的邻居就越多，也就越重要)。这种方法 k=工ag j=1 简单直观，计算的复杂度低，但是它仅仅考虑了节点 定义2节点距离定义为连接这两个节点的最 的最局部的信息，具有非常大的片面性，没有办法准 短路径上的边的数目，用d表示。 确地刻画网络中节点的重要程度。例如，“桥节点” 定义3网络的平均路径长度L定义为任意两 虽然只有两条边相连，但是在网络中处于重要的核 个节点之间距离的平均值，即 心地位。 2 2.2接近中心性 L=- ΓN(N-1) 接近中心性(closeness centrality)[ioj反映的是 定义4网络中一个度为k:的节点：的聚类系 节点在网络中居于中心的程度。它的基本思想是如 数C()定义为 果一个节点能很容易地与所有其他节点进行互动

起降的突发情况下，航空运输系统能够保持其鲁棒 性，成为人们越来越关注的问题。 刘宏鲲等［２］研究表明，中国城市航空网络具有 较大的聚类系数和较短的平均路径长度，其度分布 服从双段幂律分布，是一个具有小世界网络特性的 无标度网络； 姚红光等［３］ 通过仿真实验得出，中国 航空网络在面对随机干扰时鲁棒性较强，而在蓄意 攻击下鲁棒性较差；不同的城市节点对于网络鲁棒 性的贡献程度不同，目前有 ４０ 余个核心城市在中国 航空网络中占有举足轻重的地位。 航空网络中，准确地评估和度量节点的重要性 在提高网络的可靠性与抗毁性方面扮演着非常重要 的角色。 在由城市节点和通航城市间的直飞航线所 构成的航空网络中， 如果受突发事件的影响，某城 市节点陷入瘫痪，那么这就意味着同时取消了与该 城市节点相连的所有的航线，从而有可能引发网络 中其他通航城市之间的一些运输路径中断［４］ 。 例 如，２０１５ 年 ７ 月 １１ 日，超强台风“灿鸿”逼近上海， 受台风“灿鸿”影响，上海机场终端区的通行能力下 降 ５０％左右，共计取消航班 ３００ 多个架次。 因此，准 确评估航空网络中的重要节点，并针对其可能发生 的突发状况提前制定完备的候选方案和补救措施， 可以有效避免网络因受到外界干扰而造成航班大面 积延误，从而保证航空运输安全高效地运营。 １ 理论基础 将航空网络抽象为一个由点集 Ｖ＝ ［ｖ１ ｖ２… ｖｎ ］ 和边集 Ｅ＝ ［ｅ１ ｅ２… ｅｍ ］组成的无向图 Ｇ ＝ ［Ｖ Ｅ］，顶 点数记为 Ｎ＝ ｜Ｖ｜ ，边数记为 Ｍ ＝ ｜ Ｅ ｜ 。 图的邻接矩 阵记为 Ａｎ×ｎ ＝ （ａｉｊ），当且仅当节点 ｖｉ 与 ｖｊ 之间有连 边时 ａｉｊ ＝ １，否则 ａｉｊ ＝ ０。 定义 １ 无向网络中节点 ｖｉ 的度 ｋｉ 是指与节点 直接相连的边的数目。 它与节点的重要程度有很大 的关系。 一般而言，ｋｉ 的值越大，节点就越重要。 其 表达形式为 ｋｉ ＝ ∑ Ｎ ｊ ＝ １ ａｉｊ 定义 ２ 节点距离定义为连接这两个节点的最 短路径上的边的数目，用 ｄｉｊ表示。 定义 ３ 网络的平均路径长度 Ｌ 定义为任意两 个节点之间距离的平均值，即 Ｌ ＝ ２ Ｎ（Ｎ － １）∑ｉ≥ｊ ｄｉｊ 定义 ４ 网络中一个度为 ｋｉ 的节点 ｖｉ 的聚类系 数Ｃ（ｉ）定义为 Ｃ（ｉ） ＝ ２Ｅｉ ｋｉ（ｋｉ － １） 式中：Ｅｉ 是节点 ｖｉ 的 ｋｉ 个邻节点之间实际存在的边 数，即节点 ｖｉ 的 ｋｉ 个邻节点之间实际存在的邻居对 的数目。 聚类系数表征在网络中某一节点的两个相 邻节点也相邻的概率，反映的是网络的集聚化程度。 ２ 无向网络节点重要性指标 在复杂网络领域里评价节点重要性的方法有很 多，本质上都是源于图论和基于图的数据挖掘，主要 分为以下 ３ 类：社会网络分析、系统科学分析、信息 搜索领域分析［５］ 。 其本质上都是源于图论以及基 于图的数据挖掘，主要从网络拓扑结构入手进行 分析。 社会网络分析方法起始于 ２０ 世纪 ４０ 年代末， 在评价节点重要性的研究领域中是比较常见的。 它 主要基于这样一种假设：“重要性等价于显著性”， 即节点的重要性等价于该节点与其他节点的连接而 使其具有的显著性［６］ 。 该方法主要以网络的拓扑 结构为切入点，在不破坏网络连通性的前提下对重 要节点进行研究，并且通常不考虑节点集的重要 性［７］ 。 通过分析网络中的某种有用信息来区分不 同节点的重要性差异，其主要的分析指标包括节点 的度（ ｄｅｇｒｅｅ）、接近度（ ｃｌｏｓｅｎｅｓｓ）、介数（ ｂｅｔｗｅｅｎ⁃ ｎｅｓｓ）、特征向量（ｅｉｇｅｎｖｅｃｔｏｒ）等。 ２．１ 度中心性 度中心性（ ｄｅｇｒｅｅ ｃｅｎｔｒａｌｉｔｙ） ［８］ ，就是按照度值 的大小对节点进行排列。 它是网络中刻画节点重要 性最简单而又非常重要的指标。 具有相同度值的节 点在不同规模的网络中的重要程度是不同的，因此 为了便于比较，将节点的度中心性进行归一化处理： μＤＣ（ｉ） ＝ ｋｉ Ｎ － １ 显然，度中心性描述的是节点对于其邻居节点 的直接影响力，它认为一个节点的度值越大，与之有 直接联系的邻居就越多，也就越重要［９］ 。 这种方法 简单直观，计算的复杂度低，但是它仅仅考虑了节点 的最局部的信息，具有非常大的片面性，没有办法准 确地刻画网络中节点的重要程度。 例如，“桥节点” 虽然只有两条边相连，但是在网络中处于重要的核 心地位。 ２．２ 接近中心性 接近中心性（ ｃｌｏｓｅｎｅｓｓ ｃｅｎｔｒａｌｉｔｙ） ［１０］ 反映的是 节点在网络中居于中心的程度。 它的基本思想是如 果一个节点能很容易地与所有其他节点进行互动， 第 ５ 期 闫玲玲，等：基于度和聚类系数的中国航空网络重要性节点分析 ·５８７·

·588 智能系统学报 第11卷 那么它就处在网络的中心位置，也就是说它到其他 那么这个节点就越有影响力。与此同时，这也意味 所有节点的距离要足够短。因此，接近中心性可以 着该节点更容易发生拥塞，成为网络的瓶颈。介数 用最短距离来刻画。假设节点：和：之间的最短 中心性能够非常准确地找到网络中“流量”大的节 距离记为d,则可以计算任意一个节点心，到网络中 点，但是它的时间复杂度为O(N3),计算效率低，对 其他节点的平均最短距离： 于大型的网络并不适用 1 4w-A4, 2.4特征向量中心性 特征向量中心性(eigenvector centrality)[]是评 于是节点v的接近中心性定义为山的倒数，即： 价网络中节点重要性的一个重要指标。前面介绍的 ucc(i)= 1-N-1 几种方法把周围的邻居节点视为同等重要，仅仅从 d ∑dg (1) 邻居节点的数量上来考虑节点的重要性。而特征向 iz 该定义只能在连通的网络中使用，因此文献 量中心性同时兼顾了邻居节点的数量和质量对节点 [11]对上式进行了改进，使其能够用于非连通网络 重要性的影响，认为一个节点的重要性不仅取决于 中，即： 该节点邻居的数量，而且取决于每个邻居节点的重 要程度。特征向量中心性指标是指网络邻接矩阵对 h(i)=∑ 应其最大特征值的特征向量，即： 如果节点：和v,之间没有路径可达，则定义 4a(0= d,=o,即1/d,=0。 j=1 由上式可知，节点的接近中心性越大，表明该节 式中：入为邻接矩阵A的最大特征值，e= [e,e2…en]T为邻接矩阵A的最大特征值A对应的 点越接近网络的中心位置，那么它在网络中就越重 特征向量。 要。这一类节点与其他节点的联系并非最多，但是 2.5半局部中心性 与网络中其他节点的距离总和最短，也就是该节点 在以上提出的几种方法中，度中心性虽然简单 在网络中具有最佳视野，可以察知网络中所发生的 直观，计算的复杂度低，但只考虑了局部信息，并不 事情以及信息的流通方向。与前面的度中心性相 能准确刻画节点的重要程度。介数中心性和接近中 比，接近中心性更能反映网络的全局结构，但是这种 心性等基于全局信息的指标，虽然能够准确的定义 方法的计算复杂度较高，并且对网络的拓扑结构具 重要节点，但是由于其计算的复杂性，不能应用于大 有依赖性，例如它可以准确地发现星形网络结构的 规模的复杂网络。为了兼顾算法的准确度和计算效 中心节点，但是并不适用于随机网络。 率，Chent)等选取网络中节点的四阶邻居信息，提 2.3介数中心性 出了基于半局部信息的节点重要性排序方法，称为 介数中心性[(betweenness centrality）一般是 半局部中心性(semi-local centrality)。 指最短路径介数中心性(shortest path BC)。简单地 半局部中心性uc(i)定义为 讲，它刻画了节点对网络中沿最短路径传输的网络 流的控制力，很好地描述了网络中节点可能需要承 QG)=ΣN(o) wer(j) 载的流量。 uc(i)=∑QG) 节点：的介数定义为 jer(i) 式中：T()表示节点：的一阶邻居节点的集合， hc(i)=∑S N(心)指从出发两步内可以到达的邻居的数目， ifs,in1s1 8st 称为节点v的两层邻居度。 式中：8.代表从节点)，到v,的所有最短路径的数 相比于度中心性的一阶邻居信息，半局部中心 目，g代表从节点巴到，的g条最短路径中经过 性考虑了节点的四阶邻居信息，因此其准确性比度 的最短路径的数目。在包含n个节点的连通网络 中心性更好。于此同时，计算N(w)只需要遍历节 中，一个节点的介数最大可能取值为星形网络中心 点：.的两层邻居节点，因此其计算的复杂度相较于 节点的介数值，即(n-1)(n-2)/2。于是可以对节 介数中心性和接近中心性更低。 点心：的介数进行归一化处理： 3中国航空网络重要性节点分析 40=n-a-2 2 g 3.1网络构建与结构特性 节点的介数值越高，表明流经它的网络流越多， 以中国民用航空局官方网站公布的夏秋航季客

那么它就处在网络的中心位置，也就是说它到其他 所有节点的距离要足够短。 因此，接近中心性可以 用最短距离来刻画。 假设节点 ｖｉ 和 ｖｊ 之间的最短 距离记为 ｄｉｊ，则可以计算任意一个节点 ｖｉ 到网络中 其他节点的平均最短距离： ｄｉ ＝ １ Ｎ － １∑ ｊ≠ｉ ｄｉｊ 于是节点 ｖｉ 的接近中心性定义为 ｄｉ 的倒数，即： μＣＣ（ｉ） ＝ １ ｄｉ ＝ Ｎ － １ ∑ ｊ≠ｉ ｄｉｊ （１） 该定义只能在连通的网络中使用，因此文献 ［１１］对上式进行了改进，使其能够用于非连通网络 中，即： μＣＣ（ｉ） ＝ ∑ Ｎ ｊ ＝ １ １ ｄｉｊ 如果节点 ｖｉ 和 ｖｊ 之间没有路径可达，则定义 ｄｉｊ ＝¥，即 １ ／ ｄｉｊ ＝ ０。 由上式可知，节点的接近中心性越大，表明该节 点越接近网络的中心位置，那么它在网络中就越重 要。 这一类节点与其他节点的联系并非最多，但是 与网络中其他节点的距离总和最短，也就是该节点 在网络中具有最佳视野，可以察知网络中所发生的 事情以及信息的流通方向。 与前面的度中心性相 比，接近中心性更能反映网络的全局结构，但是这种 方法的计算复杂度较高，并且对网络的拓扑结构具 有依赖性，例如它可以准确地发现星形网络结构的 中心节点，但是并不适用于随机网络。 ２．３ 介数中心性 介数中心性［１２］ （ ｂｅｔｗｅｅｎｎｅｓｓ ｃｅｎｔｒａｌｉｔｙ） 一般是 指最短路径介数中心性（ｓｈｏｒｔｅｓｔ ｐａｔｈ ＢＣ）。 简单地 讲，它刻画了节点对网络中沿最短路径传输的网络 流的控制力，很好地描述了网络中节点可能需要承 载的流量。 节点 ｖｉ 的介数定义为 μＢＣ（ｉ） ＝ ｉ≠ｓ∑，ｉ≠ｔ，ｓ≠ｔ ｇ ｉ ｓｔ ｇｓｔ 式中：ｇｓｔ 代表从节点 ｖｓ 到 ｖｔ 的所有最短路径的数 目，ｇ ｉ ｓｔ代表从节点 ｖｓ 到 ｖｔ 的 ｇｓｔ条最短路径中经过 ｖｉ 的最短路径的数目。 在包含 ｎ 个节点的连通网络 中，一个节点的介数最大可能取值为星形网络中心 节点的介数值，即（ ｎ－１） （ ｎ－２） ／ ２。 于是可以对节 点 ｖｉ 的介数进行归一化处理： μＢＣ ′（ｉ） ＝ ２ （ｎ － １）（ｎ － ２）∑ ｇ ｉ ｓｔ ｇｓｔ 节点的介数值越高，表明流经它的网络流越多， 那么这个节点就越有影响力。 与此同时，这也意味 着该节点更容易发生拥塞，成为网络的瓶颈。 介数 中心性能够非常准确地找到网络中“流量” 大的节 点，但是它的时间复杂度为 Ｏ（Ｎ ３ ），计算效率低，对 于大型的网络并不适用。 ２．４ 特征向量中心性 特征向量中心性（ ｅｉｇｅｎｖｅｃｔｏｒ ｃｅｎｔｒａｌｉｔｙ） ［８］ 是评 价网络中节点重要性的一个重要指标。 前面介绍的 几种方法把周围的邻居节点视为同等重要，仅仅从 邻居节点的数量上来考虑节点的重要性。 而特征向 量中心性同时兼顾了邻居节点的数量和质量对节点 重要性的影响，认为一个节点的重要性不仅取决于 该节点邻居的数量， 而且取决于每个邻居节点的重 要程度。 特征向量中心性指标是指网络邻接矩阵对 应其最大特征值的特征向量，即： μＥＣ（ｉ） ＝ λ －１∑ Ｎ ｊ ＝ １ ａｉｊ ｅｊ 式中： λ 为 邻 接 矩 阵 Ａ 的 最 大 特 征 值， ｅ ＝ ［ｅ１ ｅ２… ｅｎ ］ Ｔ 为邻接矩阵 Ａ 的最大特征值 λ 对应的 特征向量。 ２．５ 半局部中心性 在以上提出的几种方法中，度中心性虽然简单 直观，计算的复杂度低，但只考虑了局部信息，并不 能准确刻画节点的重要程度。 介数中心性和接近中 心性等基于全局信息的指标，虽然能够准确的定义 重要节点，但是由于其计算的复杂性，不能应用于大 规模的复杂网络。 为了兼顾算法的准确度和计算效 率，Ｃｈｅｎ ［１３］等选取网络中节点的四阶邻居信息，提 出了基于半局部信息的节点重要性排序方法，称为 半局部中心性（ｓｅｍｉ⁃ｌｏｃａｌ ｃｅｎｔｒａｌｉｔｙ）。 半局部中心性 μＳＬＣ（ｉ）定义为 Ｑ（ｊ） ＝ ｗ∑∈Γ（ｊ） Ｎ（ｗ） μＳＬＣ（ｉ） ＝ ｊ∈∑Γ（ｉ） Ｑ（ｊ） 式中：Γ（ ｊ） 表示节点 ｖｊ 的一阶邻居节点的集合， Ｎ（ｗ）指从 ｖｗ 出发两步内可以到达的邻居的数目， 称为节点 ｖｗ 的两层邻居度。 相比于度中心性的一阶邻居信息，半局部中心 性考虑了节点的四阶邻居信息，因此其准确性比度 中心性更好。 于此同时，计算 Ｎ（ｗ）只需要遍历节 点 ｖｗ 的两层邻居节点，因此其计算的复杂度相较于 介数中心性和接近中心性更低。 ３ 中国航空网络重要性节点分析 ３．１ 网络构建与结构特性 以中国民用航空局官方网站公布的夏秋航季客 ·５８８· 智 能 系 统 学 报 第 １１ 卷

第5期 闫玲玲，等：基于度和聚类系数的中国航空网络重要性节点分析 ·589. 运航线相关数据为样本构建中国航空网络模型，其 109 中机场所在的城市为网络节点，通航城市之间的直 飞航线为网络的边。这样形成了148个节点，1153 10- 条无向边(2306条航线)的中国航空网络（见 图1)。将中国航空网络用一个148×148的邻接矩 10 阵A表示，如果节点：和之间有可达的航班，则 a=1;反之a=0,于是得到一个对称矩阵。 10 10 10 10 10 节点的度k 图2中国航空网络城市节点度分布 Fig.2 Degree distribution of Chinese aviation network 1.0* 0.9 0.8 0.7 0.6 0.5 0.4 t. 0.3 0.2 0 图1中国航空网络结构图 0 20 406080100120 Fig.1 The structure of Chinese aviation network 节点的度k 在此需要说明的是： 1)网络中所选的航线均为往返航线，因此在后 图3中国航空网络城市节点度与聚类系数相关性 期运算过程中不需要考虑航线的方向问题： Fig.3 Correlation between degree and clustering coeffi- cient of Chinese aviation network 2)对于拥有两个及以上机场的城市，将其数据 3.2中国航空网络重要性节点排序 进行合并，如上海的浦东机场和虹桥机场的数据可 下面用本文中提到的几种无向网络节点重要性 统一合并成到城市节点“上海”中。 评价指标中国航空网络模型的节点重要程度进行排 节点的度、平均路径长度和聚类系数是描述复 序，排序结果见表1。 杂网络拓扑结构最基本的特征参量。本文使用的中 节点的度反映了该机场与其他机场通航能力的 国航空网络样本，平均度为15.58，也就是说平均每 大小。中国航空网络的度分布呈现出明显的东西差 个城市机场约与其他16个城市有直接的航空联系： 异，结合中国航空网网络的空间结构，从表1中可以 Pearson相关系数[r=-0.3843,说明中国航空网 看出，度值较大的节点主要集中东部较发达地区，如 络是度一度负相关的，度值大的节点更倾向于和度 北京(102)、上海(83)、广州(83)、深圳(69)、杭州 值小的节点相连接。平均路径长度为2.2165，意味 (52)、南京(51)以及各个省会城市，如成都(61)、西 着任意两个城市机场通过不到2次转机就可以相互 安(56)、昆明(56)、重庆(56)。 连通；聚类系数为0.6877，表现出较强集聚性，说明 接近中心性是用网络中的节点到其他节点的平 中国航空网络各节点城市之间更倾向于形成短距离 均最短距离来衡量的，因此接近中心性越小，意味着 的联系5]。由此可见，中国航空网络具有较大的聚 该节点在网络中越处于中心地位，从而也就越不容 类系数和较小的平均路径长度，表现出了小世界网 易受到其他结点连通情况的控制。也就是说，接近 络特性。而图2表明，中国航空网络服从双幂律分 中心性数值较大的机场相对于数值较小的机场独立 布，具有无标度特性。 性更强，不太容易受到其他机场通航状况的影响。 中国航空网络城市节点度与聚类系数相关性如 而接近中心性TopI0的节点排序结果基本上跟度中 图3所示。可以看出，随着节点度值k的不断增加， 心性保持一致，都表现出明显的东西差异，这一点在 聚类系数C(k)的数值是不断下降的，也就是说节点 特征向量中心性和半局部中心性中都有所体现。 的度和聚类系数呈负相关。这说明在中国航空网络 节点的介数中心性反映了该机场在网络运输中 中，度值小的城市节点比度值大的城市节点更趋向 的中转和衔接能力。介数中心性高的节点在地区网 于聚集成团

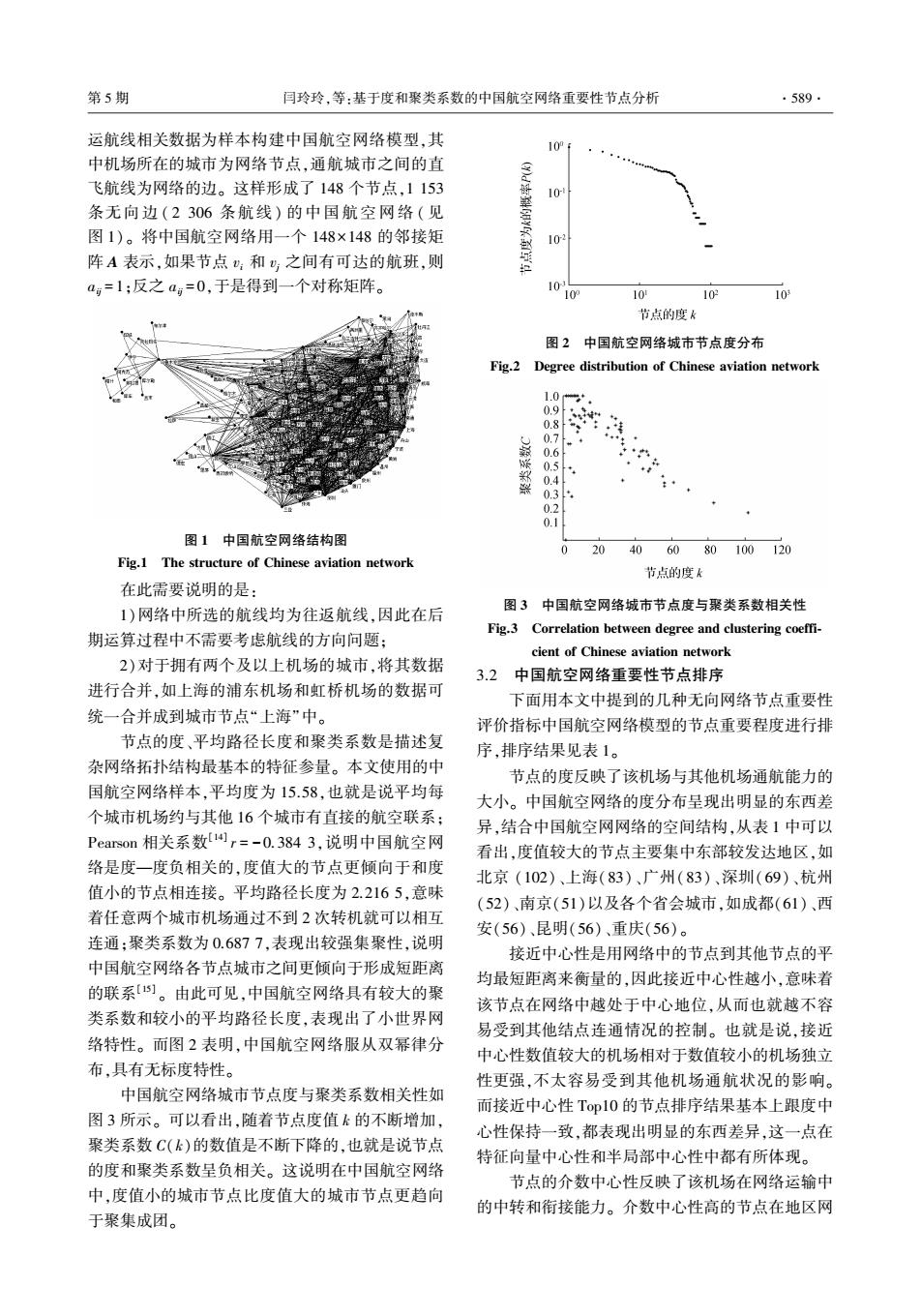
运航线相关数据为样本构建中国航空网络模型，其 中机场所在的城市为网络节点，通航城市之间的直 飞航线为网络的边。 这样形成了 １４８ 个节点，１ １５３ 条无向边 （ ２ ３０６ 条航线） 的中国航空网 络 （ 见 图 １）。 将中国航空网络用一个 １４８×１４８ 的邻接矩 阵 Ａ 表示，如果节点 ｖｉ 和 ｖｊ 之间有可达的航班，则 ａｉｊ ＝ １；反之 ａｉｊ ＝ ０，于是得到一个对称矩阵。 图 １ 中国航空网络结构图 Ｆｉｇ．１ Ｔｈｅ ｓｔｒｕｃｔｕｒｅ ｏｆ Ｃｈｉｎｅｓｅ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ 在此需要说明的是： １）网络中所选的航线均为往返航线，因此在后 期运算过程中不需要考虑航线的方向问题； ２）对于拥有两个及以上机场的城市，将其数据 进行合并，如上海的浦东机场和虹桥机场的数据可 统一合并成到城市节点“上海”中。 节点的度、平均路径长度和聚类系数是描述复 杂网络拓扑结构最基本的特征参量。 本文使用的中 国航空网络样本，平均度为 １５．５８，也就是说平均每 个城市机场约与其他 １６ 个城市有直接的航空联系； Ｐｅａｒｓｏｎ 相关系数［１４］ ｒ ＝ －０．３８４ ３，说明中国航空网 络是度—度负相关的，度值大的节点更倾向于和度 值小的节点相连接。 平均路径长度为 ２．２１６ ５，意味 着任意两个城市机场通过不到 ２ 次转机就可以相互 连通；聚类系数为 ０．６８７ ７，表现出较强集聚性，说明 中国航空网络各节点城市之间更倾向于形成短距离 的联系［１５］ 。 由此可见，中国航空网络具有较大的聚 类系数和较小的平均路径长度，表现出了小世界网 络特性。 而图 ２ 表明，中国航空网络服从双幂律分 布，具有无标度特性。 中国航空网络城市节点度与聚类系数相关性如 图 ３ 所示。 可以看出，随着节点度值 ｋ 的不断增加， 聚类系数 Ｃ（ｋ）的数值是不断下降的，也就是说节点 的度和聚类系数呈负相关。 这说明在中国航空网络 中，度值小的城市节点比度值大的城市节点更趋向 于聚集成团。 图 ２ 中国航空网络城市节点度分布 Ｆｉｇ．２ Ｄｅｇｒｅｅ ｄｉｓｔｒｉｂｕｔｉｏｎ ｏｆ Ｃｈｉｎｅｓｅ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ 图 ３ 中国航空网络城市节点度与聚类系数相关性 Ｆｉｇ．３ Ｃｏｒｒｅｌａｔｉｏｎ ｂｅｔｗｅｅｎ ｄｅｇｒｅｅ ａｎｄ ｃｌｕｓｔｅｒｉｎｇ ｃｏｅｆｆｉ⁃ ｃｉｅｎｔ ｏｆ Ｃｈｉｎｅｓｅ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ ３．２ 中国航空网络重要性节点排序 下面用本文中提到的几种无向网络节点重要性 评价指标中国航空网络模型的节点重要程度进行排 序，排序结果见表 １。 节点的度反映了该机场与其他机场通航能力的 大小。 中国航空网络的度分布呈现出明显的东西差 异，结合中国航空网网络的空间结构，从表 １ 中可以 看出，度值较大的节点主要集中东部较发达地区，如 北京 （１０２）、上海（８３）、广州（８３）、深圳（６９）、杭州 （５２）、南京（５１）以及各个省会城市，如成都（６１）、西 安（５６）、昆明（５６）、重庆（５６）。 接近中心性是用网络中的节点到其他节点的平 均最短距离来衡量的，因此接近中心性越小，意味着 该节点在网络中越处于中心地位，从而也就越不容 易受到其他结点连通情况的控制。 也就是说，接近 中心性数值较大的机场相对于数值较小的机场独立 性更强，不太容易受到其他机场通航状况的影响。 而接近中心性 Ｔｏｐ１０ 的节点排序结果基本上跟度中 心性保持一致，都表现出明显的东西差异，这一点在 特征向量中心性和半局部中心性中都有所体现。 节点的介数中心性反映了该机场在网络运输中 的中转和衔接能力。 介数中心性高的节点在地区网 第 ５ 期 闫玲玲，等：基于度和聚类系数的中国航空网络重要性节点分析 ·５８９·

·590. 智能系统学报 第11卷 络间的连接中起到了桥梁的作用。中国航空网络节 排在第七位。从空间结构上可以看出新疆地区的城市 点的介数中心性排序中，北京依然排在第1位，但是 节点大多数通过乌鲁木齐与整个航空网络连接，若移 排在第2位的乌鲁木齐在其他排序结果的前十中从 除乌鲁木齐，则新疆地区的大部分城市节点将变为孤 未出现过，排在第3位的昆明只在度中心性排序中 立节点，而昆明也同样起到非常重要的桥梁作用。 表1排名前10中国航空网络各中心性指标 Table 1 The Top10 centrality index of Chinese aviation network 介数中心性 特征向量 半局部中心性 次序城市 度中心性 城市接近中心性 城市 城市 城市 (×103) 中心性 (×10) 1北京 0.694 北京 0.762 北京 4.475 北京 0.220 北京 0.281 2上海 0.565 上海 0.693 乌鲁木齐 2.835 广州 0.207 广州 0.268 3广州 0.565 广州 0.693 昆明 2.353 上海 0.207 上海 0.267 4深圳 0.470 深圳 0.650 广州 2.231 深圳 0.196 深圳 0.257 5成都 0.415 成都 0.628 上海 2.223 成都 0.184 成都 0.245 6西安 0.381 西安 0.615 成都 1.565 南京 0.180 南京 0.242 7昆明 0.381 重庆 0.610 西安 1.508 杭州 0.178 杭州 0.240 8重庆 0.374 杭州 0.603 深圳 1.121 重庆 0.174 重庆 0.233 9杭州 0.354 南京 0.603 重庆 0.825 长沙 0.172 长沙 0.232 10南京 0.347 长沙 0.598 长沙 0.790 郑州 0.170 郑州 0.231 3.3用网络的鲁棒性和脆弱性评价排序算法 V=1/2-R 利用之前的节点重要性评价方法对中国航空网 可见，脆弱性指标的值越大，表明采用的攻击方 络的重要节点进行排序之后，分别按照节点的重要 法效果越好。于是，分别采用度中心性、接近中心 性从大到小的顺序，依次删除网络中的节点。则节 性、介数中心性、特征向量中心性和半局部中心性5 点移除后网络的破坏程度可以用最大连通子图的相 种方法对中国航空网络进行攻击，画出/n和 对大小，全局效率以及脆弱性指标来进行评价。 σ(i/n)在二维坐标上的曲线，并用脆弱性指标考察 最大连通子图概念的提出，是为了描述网络中 这5种方法的攻击效果，同时与随机攻击网络的方 的节点或连边由于一些内部或外部的原因所发生的 法得到的效果进行比较。 变化。简单来说，最大连通子图就是一个网络的众 图4为对中国航空网络模型分别进行随机攻击 多连通子图中包含节点最多的那个子图。 和蓄意攻击后，网络中移除节点的比例和最大连通 网络中，节点：和：之间的效率为两点之间最 集的规模之间的关系。在此需要说明的是，采用的 短距离的倒数，即1/d。于是网络的全局效率16就 攻击方式是同时移除i/n比例的节点，计算剩余网 定义为所有节点对效率的平均值，即 络中最大连通集所占的比例。 EG=2-m多 1 1.0 0.9 如果用i/n表示移除的节点比例，用c(i/n)表 0.8 0.7 示移除i/n比例的节点后最大连通子图的相对大 0.6 0.5 小，则该节点移除方式下网络的鲁棒性(robustness) 04 可以用R-指标)来评价。具体定义为 0.3 0.2 R=(i/m) n i=1 00.10.20.30.40.50.60.70.80.91.0 显然，无论针对哪种算法都能得到如下结果 移除节点的比例n 1-1/m 注释：1.度数中心性(0.3603)：2.介数中心性(v,0.4787) R = 2 完全图 3.接近中心性(v=0.341:4.半局部中心性(y=0.314: 5.特征向量中心性(v0.3119):6.随机攻击(，0.0243) 。11 星形图 图4移除节点比例和最大连通集规模的关系（传统方 法的攻击效果】 所以在任何网络中，无论用何种算法移除节点， Fig.4 The relationship between the proportion of removed R∈(0,1/2)。因此，文献[18]定义V-指标来衡量网 nodes and the scale of the largest connected compo- 络对所实施的节点移除方法的脆弱性(vulnerability)。 nent (Effect of traditional attack methods)

络间的连接中起到了桥梁的作用。 中国航空网络节 点的介数中心性排序中，北京依然排在第 １ 位，但是 排在第 ２ 位的乌鲁木齐在其他排序结果的前十中从 未出现过，排在第 ３ 位的昆明只在度中心性排序中 排在第七位。 从空间结构上可以看出新疆地区的城市 节点大多数通过乌鲁木齐与整个航空网络连接，若移 除乌鲁木齐，则新疆地区的大部分城市节点将变为孤 立节点，而昆明也同样起到非常重要的桥梁作用。 表 １ 排名前 １０ 中国航空网络各中心性指标 Ｔａｂｌｅ １ Ｔｈｅ Ｔｏｐ１０ ｃｅｎｔｒａｌｉｔｙ ｉｎｄｅｘ ｏｆ Ｃｈｉｎｅｓｅ ａｖｉａｔｉｏｎ ｎｅｔｗｏｒｋ 次序 城市 度中心性 城市 接近中心性 城市 介数中心性 （×１０ ３ ） 城市 特征向量 中心性 城市 半局部中心性 （×１０ ６ ） １ 北京 ０．６９４ 北京 ０．７６２ 北京 ４．４７５ 北京 ０．２２０ 北京 ０．２８１ ２ 上海 ０．５６５ 上海 ０．６９３ 乌鲁木齐 ２．８３５ 广州 ０．２０７ 广州 ０．２６８ ３ 广州 ０．５６５ 广州 ０．６９３ 昆明 ２．３５３ 上海 ０．２０７ 上海 ０．２６７ ４ 深圳 ０．４７０ 深圳 ０．６５０ 广州 ２．２３１ 深圳 ０．１９６ 深圳 ０．２５７ ５ 成都 ０．４１５ 成都 ０．６２８ 上海 ２．２２３ 成都 ０．１８４ 成都 ０．２４５ ６ 西安 ０．３８１ 西安 ０．６１５ 成都 １．５６５ 南京 ０．１８０ 南京 ０．２４２ ７ 昆明 ０．３８１ 重庆 ０．６１０ 西安 １．５０８ 杭州 ０．１７８ 杭州 ０．２４０ ８ 重庆 ０．３７４ 杭州 ０．６０３ 深圳 １．１２１ 重庆 ０．１７４ 重庆 ０．２３３ ９ 杭州 ０．３５４ 南京 ０．６０３ 重庆 ０．８２５ 长沙 ０．１７２ 长沙 ０．２３２ １０ 南京 ０．３４７ 长沙 ０．５９８ 长沙 ０．７９０ 郑州 ０．１７０ 郑州 ０．２３１ ３．３ 用网络的鲁棒性和脆弱性评价排序算法 利用之前的节点重要性评价方法对中国航空网 络的重要节点进行排序之后，分别按照节点的重要 性从大到小的顺序，依次删除网络中的节点。 则节 点移除后网络的破坏程度可以用最大连通子图的相 对大小，全局效率以及脆弱性指标来进行评价。 最大连通子图概念的提出，是为了描述网络中 的节点或连边由于一些内部或外部的原因所发生的 变化。 简单来说，最大连通子图就是一个网络的众 多连通子图中包含节点最多的那个子图。 网络中，节点 ｖｉ 和 ｖｊ 之间的效率为两点之间最 短距离的倒数，即 １ ／ ｄｉｊ。 于是网络的全局效率［１６］就 定义为所有节点对效率的平均值，即 Ｅ（Ｇ） ＝ ２ Ｎ（Ｎ － １）∑ｉ ＞ ｊ １ ｄｉｊ 如果用 ｉ ／ ｎ 表示移除的节点比例，用 σ（ｉ ／ ｎ）表 示移除 ｉ ／ ｎ 比例的节点后最大连通子图的相对大 小，则该节点移除方式下网络的鲁棒性（ｒｏｂｕｓｔｎｅｓｓ） 可以用 Ｒ⁃指标［１７］来评价。 具体定义为 Ｒ ＝ １ ｎ ∑ ｎ ｉ ＝ １ σ（ｉ ／ ｎ） 显然，无论针对哪种算法都能得到如下结果 Ｒｍａｘ ＝ １ － １ ／ ｎ ２ ， 完全图 Ｒｍｉｎ ＝ １ ｎ － １ ｎ ２ ， 星形图 ì î í ï ï ï ï 所以在任何网络中，无论用何种算法移除节点， Ｒ∈（０，１／ ２）。 因此，文献［１８］定义 Ｖ⁃指标来衡量网 络对所实施的节点移除方法的脆弱性（ｖｕｌｎｅｒａｂｉｌｉｔｙ）。 Ｖ ＝ １ ／ ２ － Ｒ 可见，脆弱性指标的值越大，表明采用的攻击方 法效果越好。 于是，分别采用度中心性、接近中心 性、介数中心性、特征向量中心性和半局部中心性 ５ 种方 法 对 中 国 航 空 网 络 进 行 攻 击， 画 出 ｉ ／ ｎ 和 σ（ｉ ／ ｎ）在二维坐标上的曲线，并用脆弱性指标考察 这 ５ 种方法的攻击效果，同时与随机攻击网络的方 法得到的效果进行比较。 图 ４ 为对中国航空网络模型分别进行随机攻击 和蓄意攻击后，网络中移除节点的比例和最大连通 集的规模之间的关系。 在此需要说明的是，采用的 攻击方式是同时移除 ｉ ／ ｎ 比例的节点，计算剩余网 络中最大连通集所占的比例。 图 ４ 移除节点比例和最大连通集规模的关系（传统方 法的攻击效果） Ｆｉｇ．４ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ｐｒｏｐｏｒｔｉｏｎ ｏｆ ｒｅｍｏｖｅｄ ｎｏｄｅｓ ａｎｄ ｔｈｅ ｓｃａｌｅ ｏｆ ｔｈｅ ｌａｒｇｅｓｔ ｃｏｎｎｅｃｔｅｄ ｃｏｍｐｏ⁃ ｎｅｎｔ （Ｅｆｆｅｃｔ ｏｆ ｔｒａｄｉｔｉｏｎａｌ ａｔｔａｃｋ ｍｅｔｈｏｄｓ） ·５９０· 智 能 系 统 学 报 第 １１ 卷