【智能系统】二阶邻居协议下多智能体系统能控能观性保持

第12卷第2期 智能系统学报 Vol.12 No.2 2017年4月 CAAI Transactions on Intelligent Systems Apr.2017 D0I:10.11992/6is.201601022 网络出版地址：http://www.cnki.net/kcms/detail/23.1538.tp.20170111.1705.012.html 二阶邻居协议下多智能体系统能控能观性保持 王康，纪志坚，晁永翠 (青岛大学自动化与电气工程学院，山东青岛266071) 摘要：为了研究多智能体系统的一致性特点及能控、能观性保持策略，分析了具有时变拓扑结构的多智能体系统 在一阶邻居协议和二阶邻居协议下的一致性速度，针对拓扑结构的特殊性，利用结构能控性性质和拉普拉斯矩阵第 二小特征值与一致性速度之间存在的关系设计出一种使能控性和能观测性保持的控制策略。此外，得出多智能体 系统在二阶邻居协议下，具有更快的一致性速度的结论。文中2个主要定理分别通过算例和仿真进行验证，算例和 仿真结果与定理结论一致。 关键词：多智能体系统：二阶邻居协议：时变拓扑结构：结构能控性：能控性：能观测性：图论 中图分类号：TP13文献标志码：A文章编号：1673-4785(2017)02-0213-08 中文引用格式：王康，纪志坚，晁永翠.二阶邻居协议下多智能体系统能控能观性保持[J].智能系统学报，2017,12(2)：213-220. 英文引用格式：WANG Kang,JI Zhijian,CHAO Yongcui..A control strategy for maitaining controllability and observability of a multi-agent system with the second-order neighborhood protocol[J].CAAI transactions on intelligent systems,2017,12(2):213- 220. A control strategy for maitaining controllability and observability of a multi-agent system with the second-order neighborhood protocol WANG Kang,JI Zhijian,CHAO Yongcui (School of Automation Engineering,Qingdao University,Qingdao 266071,China) Abstract:In order to study the characteristics of the consensus,controllability and observability of multi-agent sys- tems,we analyze the consensus speed of a multi-agent system with time-varying topologies under first-order and second-order neighborhood protocols.By utilizing the properties of the structural controllability and the relationship between the second-smallest eigenvalue of the Laplacian matrix and the consensus speed,we designed a control strategy to maintain both controllability and observability.In addition,we concluded that the multi-agent system had a faster consensus speed under the second-order neighborhood protocol.Using examples and simulations,we veri- fied the two main theorems proposed in this paper,with our observed results in full agreement with the conclusions of our theoretical analysis. Keywords:multi-agent system;second-order neighborhood protocol;time varying topologies;structural controlla- bility:controllability:observability;graph theory 近些年，随着计算机网络系统、无人机、卫星系调控制能实现我们所需要的复杂运动，因此有关多 统的高速发展，关于多智能体系统的研究也成为人 智能体系统的研究具有十分重要的意义。在研究多 们研究的热点。由于多智能体系统间各智能体的协 智能体系统时，我们利用代数图论山的知识，把多 智能体系统用拓扑图表示。其中，拓扑图的节点代 收稿日期：2016-01-13.网络出版日期：2017-01-11. 表各智能体，拓扑图的边代表各智能体间的连接关 基金项目：国家自然科学基金项目(61374062)：山东省杰出青年科学基 系。在研究过程中，产生了两个重大的结果，能控性 金项目(JQ201419). 通信作者：纪志坚.E-mail:jizhijian(@pku.org.cn. 和一致性。多智能系统的能控性首先是由

第 １２ 卷第 ２ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．２ ２０１７ 年 ４ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｐｒ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６０１０２２ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１７０１１１．１７０５．０１２．ｈｔｍｌ 二阶邻居协议下多智能体系统能控能观性保持 王康，纪志坚，晁永翠 （青岛大学 自动化与电气工程学院，山东 青岛 ２６６０７１） 摘 要：为了研究多智能体系统的一致性特点及能控、能观性保持策略，分析了具有时变拓扑结构的多智能体系统 在一阶邻居协议和二阶邻居协议下的一致性速度，针对拓扑结构的特殊性，利用结构能控性性质和拉普拉斯矩阵第 二小特征值与一致性速度之间存在的关系设计出一种使能控性和能观测性保持的控制策略。 此外，得出多智能体 系统在二阶邻居协议下，具有更快的一致性速度的结论。 文中 ２ 个主要定理分别通过算例和仿真进行验证，算例和 仿真结果与定理结论一致。 关键词：多智能体系统；二阶邻居协议；时变拓扑结构；结构能控性；能控性；能观测性；图论 中图分类号： ＴＰ１３ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０２－０２１３－０８ 中文引用格式：王康，纪志坚，晁永翠． 二阶邻居协议下多智能体系统能控能观性保持［Ｊ］． 智能系统学报， ２０１７， １２（２）： ２１３－２２０． 英文引用格式：ＷＡＮＧ Ｋａｎｇ，ＪＩ Ｚｈｉｊｉａｎ，ＣＨＡＯ Ｙｏｎｇｃｕｉ． Ａ ｃｏｎｔｒｏｌ ｓｔｒａｔｅｇｙ ｆｏｒ ｍａｉｔａｉｎｉｎｇ ｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ ａｎｄ ｏｂｓｅｒｖａｂｉｌｉｔｙ ｏｆ ａ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍ ｗｉｔｈ ｔｈｅ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｎｅｉｇｈｂｏｒｈｏｏｄ ｐｒｏｔｏｃｏｌ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（２）： ２１３－ ２２０． Ａ ｃｏｎｔｒｏｌ ｓｔｒａｔｅｇｙ ｆｏｒ ｍａｉｔａｉｎｉｎｇ ｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ ａｎｄ ｏｂｓｅｒｖａｂｉｌｉｔｙ ｏｆ ａ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍ ｗｉｔｈ ｔｈｅ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｎｅｉｇｈｂｏｒｈｏｏｄ ｐｒｏｔｏｃｏｌ ＷＡＮＧ Ｋａｎｇ， ＪＩ Ｚｈｉｊｉａｎ， ＣＨＡＯ Ｙｏｎｇｃｕｉ （Ｓｃｈｏｏｌ ｏｆ Ａｕｔｏｍａｔｉｏｎ Ｅｎｇｉｎｅｅｒｉｎｇ， Ｑｉｎｇｄａｏ Ｕｎｉｖｅｒｓｉｔｙ， Ｑｉｎｇｄａｏ ２６６０７１， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｏｒｄｅｒ ｔｏ ｓｔｕｄｙ ｔｈｅ ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ ｏｆ ｔｈｅ ｃｏｎｓｅｎｓｕｓ， ｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ ａｎｄ ｏｂｓｅｒｖａｂｉｌｉｔｙ ｏｆ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓ⁃ ｔｅｍｓ， ｗｅ ａｎａｌｙｚｅ ｔｈｅ ｃｏｎｓｅｎｓｕｓ ｓｐｅｅｄ ｏｆ ａ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍ ｗｉｔｈ ｔｉｍｅ⁃ｖａｒｙｉｎｇ ｔｏｐｏｌｏｇｉｅｓ ｕｎｄｅｒ ｆｉｒｓｔ⁃ｏｒｄｅｒ ａｎｄ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｎｅｉｇｈｂｏｒｈｏｏｄ ｐｒｏｔｏｃｏｌｓ． Ｂｙ ｕｔｉｌｉｚｉｎｇ ｔｈｅ ｐｒｏｐｅｒｔｉｅｓ ｏｆ ｔｈｅ ｓｔｒｕｃｔｕｒａｌ ｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ ａｎｄ ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ｓｅｃｏｎｄ⁃ｓｍａｌｌｅｓｔ ｅｉｇｅｎｖａｌｕｅ ｏｆ ｔｈｅ Ｌａｐｌａｃｉａｎ ｍａｔｒｉｘ ａｎｄ ｔｈｅ ｃｏｎｓｅｎｓｕｓ ｓｐｅｅｄ， ｗｅ ｄｅｓｉｇｎｅｄ ａ ｃｏｎｔｒｏｌ ｓｔｒａｔｅｇｙ ｔｏ ｍａｉｎｔａｉｎ ｂｏｔｈ ｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ ａｎｄ ｏｂｓｅｒｖａｂｉｌｉｔｙ． Ｉｎ ａｄｄｉｔｉｏｎ， ｗｅ ｃｏｎｃｌｕｄｅｄ ｔｈａｔ ｔｈｅ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍ ｈａｄ ａ ｆａｓｔｅｒ ｃｏｎｓｅｎｓｕｓ ｓｐｅｅｄ ｕｎｄｅｒ ｔｈｅ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｎｅｉｇｈｂｏｒｈｏｏｄ ｐｒｏｔｏｃｏｌ． Ｕｓｉｎｇ ｅｘａｍｐｌｅｓ ａｎｄ ｓｉｍｕｌａｔｉｏｎｓ， ｗｅ ｖｅｒｉ⁃ ｆｉｅｄ ｔｈｅ ｔｗｏ ｍａｉｎ ｔｈｅｏｒｅｍｓ ｐｒｏｐｏｓｅｄ ｉｎ ｔｈｉｓ ｐａｐｅｒ， ｗｉｔｈ ｏｕｒ ｏｂｓｅｒｖｅｄ ｒｅｓｕｌｔｓ ｉｎ ｆｕｌｌ ａｇｒｅｅｍｅｎｔ ｗｉｔｈ ｔｈｅ ｃｏｎｃｌｕｓｉｏｎｓ ｏｆ ｏｕｒ ｔｈｅｏｒｅｔｉｃａｌ ａｎａｌｙｓｉｓ． Ｋｅｙｗｏｒｄｓ： ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍ； ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｎｅｉｇｈｂｏｒｈｏｏｄ ｐｒｏｔｏｃｏｌ； ｔｉｍｅ ｖａｒｙｉｎｇ ｔｏｐｏｌｏｇｉｅｓ； ｓｔｒｕｃｔｕｒａｌ ｃｏｎｔｒｏｌｌａ⁃ ｂｉｌｉｔｙ； ｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ； ｏｂｓｅｒｖａｂｉｌｉｔｙ； ｇｒａｐｈ ｔｈｅｏｒｙ 收稿日期：２０１６－０１－１３． 网络出版日期：２０１７－０１－１１． 基金项目：国家自然科学基金项目（６１３７４０６２）；山东省杰出青年科学基 金项目（ＪＱ２０１４１９）． 通信作者：纪志坚．Ｅ⁃ｍａｉｌ：ｊｉｚｈｉｊｉａｎ＠ ｐｋｕ．ｏｒｇ．ｃｎ． 近些年，随着计算机网络系统、无人机、卫星系 统的高速发展，关于多智能体系统的研究也成为人 们研究的热点。 由于多智能体系统间各智能体的协 调控制能实现我们所需要的复杂运动，因此有关多 智能体系统的研究具有十分重要的意义。 在研究多 智能体系统时，我们利用代数图论［１］ 的知识，把多 智能体系统用拓扑图表示。 其中，拓扑图的节点代 表各智能体，拓扑图的边代表各智能体间的连接关 系。 在研究过程中，产生了两个重大的结果，能控性 和一 致 性。 多 智 能 系 统 的 能 控 性 首 先 是 由

.214 智能系统学报 第12卷 Tannert)提出来的，通过利用经典能控性概念，把拉 体系统的能控性和能观测性得到保持。这对于易受 普拉斯矩阵分块为子矩阵，得到能控性判据。近年 外界环境干扰的多智能体系统的研究具有较高的理 来，多智能体系统的能控性研究受到国内外科研工 论价值。 作者的广泛关注3-)。然而，在能控性保持方面的 1预备知识 研究工作则刚刚起步，目前主要是以L.Sabatti- ni9]的研究为主。 在这篇文章中，我们所研究的拓扑图都是初始 一致性问题的研究可以追潮到20世纪70年代 状态连通的无向图。无向图可以用G= 的管理科学和统计领域[3。目前关于一致性问 (V,E,A)表示，其中，集合V表示图的节点集，集合 题的研究很大程度上以T.Vicsek[1]提出的Vicsek E表示连接节点的边集，E={e1,e2,…,e},矩阵 模型为基础。多智能体系统的一致性主要是研究如 A=[a:]为图G的邻接矩阵，其中元素ag为节点： 何基于多智能体系统中个体之间有限的信息交换， 与U之间的边的权重。令矩阵D=[d]为图G的度 实现所有智能体的某个或某些状态量趋于相等的问 矩阵，且当i=j时，元素d表示为节点：的度数；当 题。对一致性协议的研究能让我们清楚地了解到智 i≠j时，d=0。 能体之间信息交换的过程。Olfati-Sabert6提出了 拉普拉斯矩阵是表示拓扑图节点与边关系的一 解决多智能体网络系统的一致性协议的理论框架， 种矩阵，也是我们研究多智能体系统需要借助的一 并且得到在连续时间一阶多智能体系统中，当通信 个重要概念。对于一个包含N个节点的无向图G, 拓扑结构表示的图为无向图时，多智能体系统的一 其拉普拉斯矩阵定义为L=D-A,拉普拉斯矩阵还 致速度取决于图的拉普拉斯矩阵的第二小特征值的 可以表示为L=严1，其中矩阵I=[i]表示把无向 结论，即一致性速度与拓扑图的拉普拉斯矩阵第二 图G规定为具有任意方向有向图的关联矩阵，元素 小特征值入，之间存在正相关的关系。同时在文献 1 x:是e的起点 [1,16-18]中，对第二小特征值入2的物理意义也做 -1, x:是e的终点 出了说明，并指出了入，不仅可以度量一致性速度， 0, x:与e不相关 也可以表示智能体系统的稳定性。 拉普拉斯矩阵具有如下性质： 在一致性问题中，以一阶邻居协议的研究最为 1)对于一个所有元素均为1的列向量，L与该 普遍，即考虑智能体的邻居信息。一阶邻居协议具 列向量的乘积为零矩阵； 有适用面广泛、作用原理简单的优点。然而由于多 2)令入1，入2，…，入w为拉普拉斯矩阵的特征值， 智能体系统越来越复杂，一阶邻居协议的信息交换 则0=入1≤入2≤…≤入N: 方式已经不能满足我们的需要，例如在复杂的全球 3)第1个非零特征值（第2个最小的特征值 卫星网络(GPS)中，采用一阶邻居协议显然会使信 入z)称为代数连通度。 息的交换效率低下，整个卫星系统协同控制效果并 文中对二阶邻居协议下的多智能体系统进行了 不好。而采用二阶邻居协议，由于系统收敛性比前 讨论。因此，我们需要掌握合并图的概念。合并图 者更好，这就为复杂卫星网络系统的运转提供更高 是由节点与实际边组成的实际图g和节点与虚拟边 效的保障。因此，对二阶邻居协议的研究就显得尤 组成的虚拟图g。构成。因此，合并图的拉普拉斯矩 为重要。和一阶邻居协议相比，二阶邻居协议不仅 阵L。分别由图G中实际图的拉普拉斯矩阵L和虚 利用智能体邻居的信息，还利用其二阶邻居的信息， 拟图的拉普拉斯矩阵i构成。即L.=L+i。记D 而系统实际的通信拓扑结构并未发生变化。本文通 过对上述两种一致性协议进行比较，得出了多智能 和A为虚拟图的度矩阵和邻接矩阵，D和A为实际 体系统采用二阶邻居协议时，多智能体系统中各智 图的度矩阵和邻接矩阵，那么L=(D+D)- 能体达到一致性速度更快的结论。同时，针对现实 (A+A)。 中具有时变拓扑结构的系统，为了使网络系统能够 更稳定运转，避免受外部环境的影响，以达到人们需 2系统模型 要的工作状态，这就对系统的能控性和能观测性提 考虑具有N个智能体的多智能体系统，并且此 出了很大要求，就需要领航者对跟随者的控制能力 系统可以用无向图G=(V,E,A)表示。记x:为第i 一直保持下去。本文通过借助结构能控性的概念和 个智能体的状态，每个智能体的状态遵循如下一阶 性质90)，设计了一种全新的控制策略，使多智能 动力学方程：

Ｔａｎｎｅｒ ［２］提出来的，通过利用经典能控性概念，把拉 普拉斯矩阵分块为子矩阵，得到能控性判据。 近年 来，多智能体系统的能控性研究受到国内外科研工 作者的广泛关注［３－８］ 。 然而，在能控性保持方面的 研究工作则 刚 刚 起 步， 目 前 主 要 是 以 Ｌ． Ｓａｂａｔｔｉ⁃ ｎｉ ［９－１２］的研究为主。 一致性问题的研究可以追溯到 ２０ 世纪 ７０ 年代 的管理科学和统计领域［１３－１４］ 。 目前关于一致性问 题的研究很大程度上以 Ｔ．Ｖｉｃｓｅｋ ［１５］ 提出的 Ｖｉｃｓｅｋ 模型为基础。 多智能体系统的一致性主要是研究如 何基于多智能体系统中个体之间有限的信息交换， 实现所有智能体的某个或某些状态量趋于相等的问 题。 对一致性协议的研究能让我们清楚地了解到智 能体之间信息交换的过程。 Ｏｌｆａｔｉ⁃Ｓａｂｅｒ ［１６］ 提出了 解决多智能体网络系统的一致性协议的理论框架， 并且得到在连续时间一阶多智能体系统中，当通信 拓扑结构表示的图为无向图时，多智能体系统的一 致速度取决于图的拉普拉斯矩阵的第二小特征值的 结论，即一致性速度与拓扑图的拉普拉斯矩阵第二 小特征值 λ２ 之间存在正相关的关系。 同时在文献 ［１，１６－１８］中，对第二小特征值 λ２ 的物理意义也做 出了说明，并指出了 λ２ 不仅可以度量一致性速度， 也可以表示智能体系统的稳定性。 在一致性问题中，以一阶邻居协议的研究最为 普遍，即考虑智能体的邻居信息。 一阶邻居协议具 有适用面广泛、作用原理简单的优点。 然而由于多 智能体系统越来越复杂，一阶邻居协议的信息交换 方式已经不能满足我们的需要，例如在复杂的全球 卫星网络（ＧＰＳ）中，采用一阶邻居协议显然会使信 息的交换效率低下，整个卫星系统协同控制效果并 不好。 而采用二阶邻居协议，由于系统收敛性比前 者更好，这就为复杂卫星网络系统的运转提供更高 效的保障。 因此，对二阶邻居协议的研究就显得尤 为重要。 和一阶邻居协议相比，二阶邻居协议不仅 利用智能体邻居的信息，还利用其二阶邻居的信息， 而系统实际的通信拓扑结构并未发生变化。 本文通 过对上述两种一致性协议进行比较，得出了多智能 体系统采用二阶邻居协议时，多智能体系统中各智 能体达到一致性速度更快的结论。 同时，针对现实 中具有时变拓扑结构的系统，为了使网络系统能够 更稳定运转，避免受外部环境的影响，以达到人们需 要的工作状态，这就对系统的能控性和能观测性提 出了很大要求，就需要领航者对跟随者的控制能力 一直保持下去。 本文通过借助结构能控性的概念和 性质［１９－２０］ ，设计了一种全新的控制策略，使多智能 体系统的能控性和能观测性得到保持。 这对于易受 外界环境干扰的多智能体系统的研究具有较高的理 论价值。 １ 预备知识 在这篇文章中，我们所研究的拓扑图都是初始 状 态 连 通 的 无 向 图。 无 向 图 可 以 用 Ｇ ＝ (Ｖ，Ｅ，Ａ) 表示，其中，集合 Ｖ 表示图的节点集，集合 Ｅ 表示连接节点的边集， Ｅ ＝ ｅ１ ，ｅ２ ，…，ｅｊ { } ，矩阵 Ａ ＝ ａｉｊ [ ] 为图 Ｇ 的邻接矩阵，其中元素 ａｉｊ 为节点 ｖｉ 与 ｖｊ 之间的边的权重。 令矩阵 Ｄ ＝ ｄｉｊ [ ] 为图 Ｇ 的度 矩阵，且当 ｉ ＝ ｊ 时，元素 ｄｉｊ 表示为节点 ｖｉ 的度数；当 ｉ ≠ ｊ 时， ｄｉｊ ＝ ０。 拉普拉斯矩阵是表示拓扑图节点与边关系的一 种矩阵，也是我们研究多智能体系统需要借助的一 个重要概念。 对于一个包含 Ｎ 个节点的无向图 Ｇ ， 其拉普拉斯矩阵定义为 Ｌ ＝ Ｄ － Ａ ，拉普拉斯矩阵还 可以表示为 Ｌ ＝ Ｉ Ｔ Ｉ ，其中矩阵 Ｉ ＝ ［ｉ ｉｊ］ 表示把无向 图 Ｇ 规定为具有任意方向有向图的关联矩阵，元素 ｉ ｉｊ ＝ １ ， ｘｉ 是 ｅｊ 的起点 － １， ｘｉ 是 ｅｊ 的终点 ０ ， ｘｉ 与 ｅｊ 不相关 ì î í ï ï ï ï 拉普拉斯矩阵具有如下性质： １）对于一个所有元素均为 １ 的列向量， Ｌ 与该 列向量的乘积为零矩阵； ２）令 λ１ ，λ２ ，…，λ Ｎ 为拉普拉斯矩阵的特征值， 则 ０ ＝ λ１ ≤ λ２ ≤ … ≤ λ Ｎ ； ３）第 １ 个非零特征值（第 ２ 个最小的特征值 λ２ ） 称为代数连通度。 文中对二阶邻居协议下的多智能体系统进行了 讨论。 因此，我们需要掌握合并图的概念。 合并图 是由节点与实际边组成的实际图 ｇ 和节点与虚拟边 组成的虚拟图 ｇｖ 构成。 因此，合并图的拉普拉斯矩 阵 Ｌｃ 分别由图 Ｇ 中实际图的拉普拉斯矩阵 Ｌ 和虚 拟图的拉普拉斯矩阵 Ｌ ～ 构成。 即 Ｌｃ ＝ Ｌ ＋ Ｌ ～ 。 记 Ｄ ～ 和 Ａ ～ 为虚拟图的度矩阵和邻接矩阵， Ｄ 和 Ａ 为实际 图的 度 矩 阵 和 邻 接 矩 阵， 那 么 Ｌｃ ＝ Ｄ ＋ Ｄ ～ ( ) － Ａ ＋ Ａ ～ ( ) 。 ２ 系统模型 考虑具有 Ｎ 个智能体的多智能体系统，并且此 系统可以用无向图 Ｇ ＝ (Ｖ，Ｅ，Ａ) 表示。 记 ｘｉ 为第 ｉ 个智能体的状态，每个智能体的状态遵循如下一阶 动力学方程： ·２１４· 智 能 系 统 学 报 第 １２ 卷

第2期 王康，等：二阶邻居协议下多智能体系统能控能观性保持 ·215 x:(t)=u:(t),i=1,2,…,n (1) x'LX 入，(G)=min 式中x:(t)和4，(t)分别为智能体i的状态和输入。 ≠0IxI2 1x=0 设N:为智能体i的邻居集，即N:= 即入2(G)‖x‖2≤x'Lx,故 行∈V(G)I(,)∈E(G)}。那么在一阶邻居协 议下， V(x)≤-A2(G)IxI2=-2A2(G)V(x)≤0 所以x的状态与入，相关，当V(x)<0时，说明系统 u,()=-∑0x,)-x()),i=1,2,…,n jeN 渐近稳定且以速度入2进行收敛，当V(x)=0时，说 (2) 明x的状态为0，x:=,即系统中每个智能体达到 设N为智能体i的二阶邻居集，即N好= 一 致性状态。 {k∈k∈yJ∈N:,k≠i,k年N}。所以各智 证毕。 能体之间通过二阶邻居一致性协议进行下式连接： 定理1对于一阶多智能体系统(1)，它在二阶 0=-w-0)A.(0- 邻居协议(3)下达到一致性的速度比在一阶邻居协 议(2)下更快。 x(t)),i=1,2,…,n (3) 证明对于一个具有N个节点的无向图G,假 设在一阶邻居协议(2)下它的拉普拉斯矩阵为L, 式中：心，为实际图中节点之间的权值，wk为虚拟图 关联矩阵为I,那么x'Lx=x'Ix=(I'x)Tx。因 节点之间权值。 为对于任意两个节点x:和x,1=±[-11]，所 在式(3)中，每个智能体在获取自己的状态信 以1x=±(x:-x),即xx=∑(x,-)2。根 息时不仅利用其邻居的状态信息，还利用其二阶邻 ijeE(G) 居的状态信息。由于智能体i与其二阶邻居之间并 据拉普拉斯矩阵的性质2，可得入，(G)= 不存在实际的通信链路，所以智能体i的二阶邻居 (x:-x)2 ie(G) 的信息由智能体i的邻居间接传递给i。由式(1) -i=1,2,…,n,对于无向连通图 和式(3)，系统中每个智能体的状态可以表示为 ,()=-∑0，(x,()-()-∑0(x(t)- G,入2可以表示为 jeN ke好 ∑(x-x)2 x(t)),i=1,2,…,n (4) A2(G)=min (6) x≠0 ∑好 1x=0 令w=10t=1,则 在二阶邻居协议(3)下，节点x:不仅考虑与它 x(0)=- 三x@-)-④) 邻居节点x间的连接关系，还需要考虑与二阶邻居 keN 节点x之间的连接关系。因此，如果k∈ x(t)）,i=1,2,…,n E(g)时，其中i为虚拟图g。的关联矩阵。所以 所以系统可以写为如下这种形式： xLx=x(L+L)x= x(t)=-Lx(t)-Lx(t)= ∑(x-x)2+∑(x-)2 ikeE(g:) -(L+L)x(t)=-Lx(i) (5) 因此 引理116)]拉普拉斯矩阵L.的第二小特征值 ∑x-x)2+∑(x-x)2 入，可用于表征系统一致收敛的速度。 jeE(C ikeE(g) 入，(G)=min 证明构造一个李雅普诺夫函数： x*0 1Tx=0 ∑ =r7=方Ix (7) 显然，式(7)大于式(6)，即多智能体系统在二 对此函数求导可得 阶邻居协议下达到一致性的速度比在一阶邻居协议 +x1: )=r)x 下更快。证毕。 我们也可以借助例子对定理1做进一步理解。 结合式(5)得 对于具有4个节点的多智能体系统(1)，假设各智 V(x)=-xLx 能体在t=0时刻的状态分别为x(0)= 因为图G是无向连通图，所以6： [51-6-8]T。通过借助MATLAB可以分

ｘ · ｉ (ｔ) ＝ ｕｉ (ｔ) ， ｉ ＝ １，２，…，ｎ （１） 式中 ｘｉ (ｔ) 和 ｕｉ (ｔ) 分别为智能体 ｉ 的状态和输入。 设 Ｎｉ 为 智 能 体 ｉ 的 邻 居 集， 即 Ｎｉ ＝ ｊ ∈ Ｖ(Ｇ) ｖｉ，ｖｊ { ( ) ∈ Ｅ(Ｇ) } 。 那么在一阶邻居协 议下， ｕｉ (ｔ) ＝ － ∑ ｊ∈Ｎｉ ｗｉｊ ｘｉ (ｔ) － ｘｊ ( (ｔ) ) ，ｉ ＝ １，２，…，ｎ （２） 设 Ｎ ２ ｉ 为 智 能 体 ｉ 的 二 阶 邻 居 集， 即 Ｎ ２ ｉ ＝ ｋ ∈ ｖ ｋ ∈ Ｎｊ，ｊ ∈ Ｎｉ，ｋ ≠ ｉ，ｋ ∉ Ｎｉ { } 。 所以各智 能体之间通过二阶邻居一致性协议进行下式连接： ｕｉ（ｔ） ＝ － ∑ ｊ∈Ｎｉ ｗｉｊ（ｘｉ（ｔ） － ｘｊ（ｔ）） － ∑ｋ∈Ｎ２ ｉ ｗｉｋ（ｘｉ（ｔ） － ｘｋ（ｔ）），ｉ ＝ １，２，…，ｎ （３） 式中： ｗｉｊ 为实际图中节点之间的权值， ｗｉｋ 为虚拟图 节点之间权值。 在式（３）中，每个智能体在获取自己的状态信 息时不仅利用其邻居的状态信息，还利用其二阶邻 居的状态信息。 由于智能体 ｉ 与其二阶邻居之间并 不存在实际的通信链路，所以智能体 ｉ 的二阶邻居 的信息由智能体 ｉ 的邻居间接传递给 ｉ 。 由式（１） 和式（３），系统中每个智能体的状态可以表示为 ｘ · ｉ（ｔ） ＝ － ∑ ｊ∈Ｎｉ ｗｉｊ（ｘｉ（ｔ） － ｘｊ（ｔ）） － ∑ｋ∈Ｎ２ ｉ ｗｉｋ（ｘｉ（ｔ） － ｘｋ（ｔ）），ｉ ＝ １，２，…，ｎ （４） 令 ｗｉｊ ＝ ｗｉｋ ＝ １，则 ｘ · ｉ（ｔ） ＝ － ∑ ｊ∈Ｎｉ （ｘｉ（ｔ） － ｘｊ（ｔ）） － ∑ｋ∈Ｎ２ ｉ （ｘｉ（ｔ） － ｘｋ（ｔ）），ｉ ＝ １，２，…，ｎ 所以系统可以写为如下这种形式： ｘ · （ｔ） ＝ － Ｌｘ（ｔ） － Ｌ ～ ｘ（ｔ） ＝ － （Ｌ ＋ Ｌ ～ ）ｘ（ｔ） ＝ － Ｌｃｘ（ｔ） （５） 引理 １ ［１６］ 拉普拉斯矩阵 Ｌｃ 的第二小特征值 λ２ 可用于表征系统一致收敛的速度。 证明 构造一个李雅普诺夫函数： Ｖ(ｘ) ＝ ｘ Ｔ １ ２ ｘ ＝ １ ２ ‖ｘ‖２ 对此函数求导可得 Ｖ · (ｘ) ＝ ｘ ·Ｔ １ ２ ｘ ＋ ｘ Ｔ １ ２ ｘ · 结合式（５）得 Ｖ · (ｘ) ＝ － ｘ ＴＬｃｘ 因为图 Ｇ 是无向连通图，所以［１６］ ： λ２ (Ｇ) ＝ ｍｉｎ ｘ≠０ １ Ｔｘ ＝ ０ ｘ ＴＬｃｘ ‖ｘ‖２ 即 λ２ (Ｇ) ‖ｘ‖２ ≤ ｘ ＴＬｘ ，故 Ｖ · (ｘ) ≤－ λ２ (Ｇ) ‖ｘ‖２ ＝ － ２λ２ (Ｇ) Ｖ(ｘ) ≤ ０ 所以 ｘ 的状态与 λ２ 相关，当 Ｖ · (ｘ) ＜ ０ 时，说明系统 渐近稳定且以速度 λ２ 进行收敛，当 Ｖ · (ｘ) ＝ ０ 时，说 明 ｘ 的状态为 ０， ｘｉ ＝ ｘｊ ，即系统中每个智能体达到 一致性状态。 证毕。 定理 １ 对于一阶多智能体系统（１），它在二阶 邻居协议（３）下达到一致性的速度比在一阶邻居协 议（２）下更快。 证明 对于一个具有 Ｎ 个节点的无向图 Ｇ ，假 设在一阶邻居协议（２）下它的拉普拉斯矩阵为 Ｌ ， 关联矩阵为 Ｉ ，那么 ｘ ＴＬｘ ＝ ｘ Ｔ ＩＩ Ｔ ｘ ＝ （Ｉ Ｔ ｘ） Ｔ Ｉ Ｔ ｘ 。 因 为对于任意两个节点 ｘｉ 和 ｘｊ ， Ｉ ＝ ± [ － １ １] ，所 以 Ｉ Ｔ ｘ ＝ ± ｘｉ － ｘｊ ( ) ，即 ｘ ＴＬｘ ＝ ｉｊ∈∑Ｅ（Ｇ） ｘｉ － ｘｊ ( ) ２ 。 根 据 拉 普 拉 斯 矩 阵 的 性 质 ２， 可 得 λｉ (Ｇ) ＝ ∑ｉｊ∈Ｅ (Ｇ ) ｘｉ － ｘｊ ( ) ２ ∑ｉ ｘ ２ ｉ ｉ ＝ １，２，…，ｎ ，对于无向连通图 Ｇ ， λ２ 可以表示为 λ２ (Ｇ) ＝ ｍｉｎ ｘ≠０ １ Ｔｘ ＝ ０ ∑ｉｊ∈Ｅ (Ｇ ) ｘｉ － ｘｊ ( ) ２ ∑ｉ ｘ ２ ｉ （６） 在二阶邻居协议（３）下，节点 ｘｉ 不仅考虑与它 邻居节点 ｘｊ 间的连接关系，还需要考虑与二阶邻居 节点 ｘｋ 之 间 的 连 接 关 系。 因 此， 如 果 ｉｋ ∈ Ｅ ｇｖ ( ) 时， 其中 Ｉ ～ 为虚拟图 ｇｖ 的关联矩阵。 所以 ｘ ＴＬｃｘ ＝ ｘ Ｔ Ｌ ＋ Ｌ ～ ( ) ｘ ＝ ∑ｉｊ∈Ｅ (Ｇ ) ｘｉ － ｘｊ ( ) ２ ＋ ∑ｉｋ∈Ｅ ｇｖ ( ) ｘｉ － ｘｊ ( ) ２ 因此 λ２ (Ｇ) ＝ ｍｉｎ ｘ≠０ １ Ｔｘ ＝ ０ ∑ｉｊ∈Ｅ (Ｇ ) ｘｉ － ｘｊ ( ) ２ ＋ ∑ｉｋ∈Ｅ ｇｖ ( ) ｘｉ － ｘｋ ( ) ２ ∑ｉ ｘ ２ ｉ （７） 显然，式（７）大于式（６），即多智能体系统在二 阶邻居协议下达到一致性的速度比在一阶邻居协议 下更快。 证毕。 我们也可以借助例子对定理 １ 做进一步理解。 对于具有 ４ 个节点的多智能体系统（１），假设各智 能 体 在 ｔ ＝ ０ 时 刻 的 状 态 分 别 为 ｘ(０) ＝ [５ １ － ６ － ８] Ｔ 。 通过借助 ＭＡＴＬＡＢ 可以分 第 ２ 期 王康，等： 二阶邻居协议下多智能体系统能控能观性保持 ·２１５·

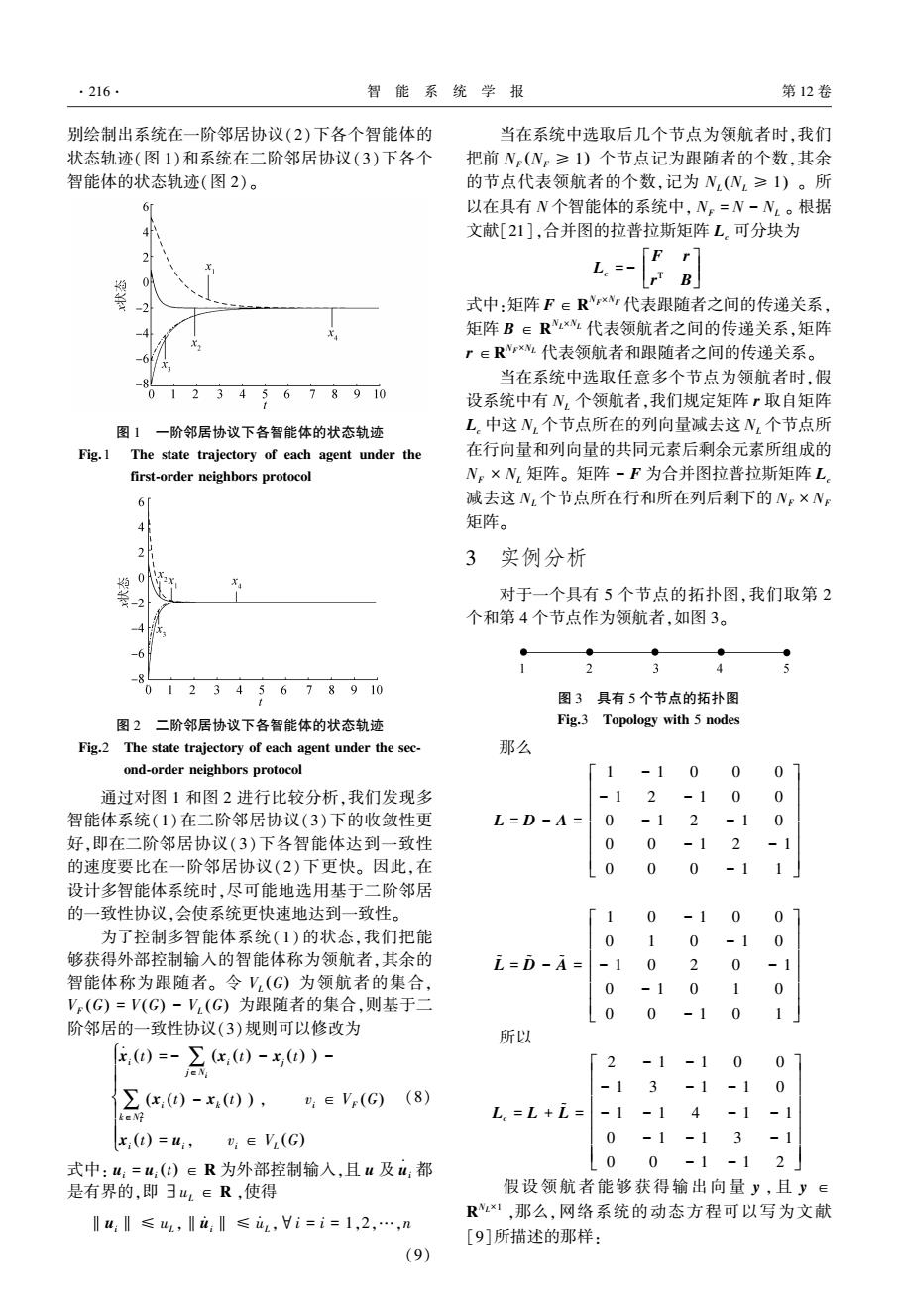
216 智能系统学报 第12卷 别绘制出系统在一阶邻居协议(2)下各个智能体的 当在系统中选取后几个节点为领航者时，我们 状态轨迹（图1）和系统在二阶邻居协议(3)下各个 把前N(N。≥1)个节点记为跟随者的个数，其余 智能体的状态轨迹（图2）。 的节点代表领航者的个数，记为N,(N,≥1)。所 6 以在具有N个智能体的系统中，N=N-N,。根据 文献[21]，合并图的拉普拉斯矩阵L.可分块为 L。=- 「Fr r B 式中：矩阵F∈Rxr代表跟随者之间的传递关系， 矩阵B∈Rx,代表领航者之间的传递关系，矩阵 r∈Rrx代表领航者和跟随者之间的传递关系。 当在系统中选取任意多个节点为领航者时，假 012345678910 设系统中有N,个领航者，我们规定矩阵r取自矩阵 图1一阶邻居协议下各智能体的状态轨迹 L.中这N,个节点所在的列向量减去这N个节点所 Fig.1 The state trajectory of each agent under the 在行向量和列向量的共同元素后剩余元素所组成的 first-order neighbors protocol Np×N,矩阵。矩阵-F为合并图拉普拉斯矩阵L 6 减去这N,个节点所在行和所在列后剩下的Ne×Ne 4 矩阵。 3实例分析 0 装2 对于一个具有5个节点的拓扑图，我们取第2 个和第4个节点作为领航者，如图3。 -4 -6 1 2 3 4 5 012345678910 图3具有5个节点的拓扑图 图2二阶邻居协议下各智能体的状态轨迹 Fig.3 Topology with 5 nodes Fig.2 The state trajectory of each agent under the sec- 那么 ond-order neighbors protocol 「1 -1 0 0 0 通过对图1和图2进行比较分析，我们发现多 -1 2 -1 0 0 智能体系统(1)在二阶邻居协议(3)下的收敛性更 L=D-A= 0 -1 2 -1 0 好，即在二阶邻居协议(3)下各智能体达到一致性 0 0 -1 2 的速度要比在一阶邻居协议(2)下更快。因此，在 0 0 0 -1 设计多智能体系统时，尽可能地选用基于二阶邻居 的一致性协议，会使系统更快速地达到一致性。 「1 0 -1 0 0 为了控制多智能体系统(1)的状态，我们把能 0 1 0 -1 0 够获得外部控制输入的智能体称为领航者，其余的 i=D-A= -1 0 2 -1 智能体称为跟随者。令V,(G)为领航者的集合， 0 -1 0 0 V(G)=V(G)-V,(G)为跟随者的集合，则基于二 0 0 -1 0 1 阶邻居的一致性协议(3)规则可以修改为 所以 )=-∑(c,()-x0)- 「 2 -1 -1 0 0 -1 3 -1 -1 ∑(c,(0)-x()),:eV(G) (8) 0 e好 L。=L+i= -1-1 4 -1-1 x,(t)=:,:eV(G) 0 -1 -13 -1 式中：u:=u:(t)∈R为外部控制输人，且u及u:都 L00 -1 -12J 是有界的，即3u,∈R,使得 假设领航者能够获得输出向量y,且y∈ Rx1,那么，网络系统的动态方程可以写为文献 ‖w:‖≤u,la:‖≤i,i=i=1,2,…,n [9]所描述的那样： (9)

别绘制出系统在一阶邻居协议（２）下各个智能体的 状态轨迹（图 １）和系统在二阶邻居协议（３）下各个 智能体的状态轨迹（图 ２）。 图 １ 一阶邻居协议下各智能体的状态轨迹 Ｆｉｇ．１ Ｔｈｅ ｓｔａｔｅ ｔｒａｊｅｃｔｏｒｙ ｏｆ ｅａｃｈ ａｇｅｎｔ ｕｎｄｅｒ ｔｈｅ ｆｉｒｓｔ⁃ｏｒｄｅｒ ｎｅｉｇｈｂｏｒｓ ｐｒｏｔｏｃｏｌ 图 ２ 二阶邻居协议下各智能体的状态轨迹 Ｆｉｇ．２ Ｔｈｅ ｓｔａｔｅ ｔｒａｊｅｃｔｏｒｙ ｏｆ ｅａｃｈ ａｇｅｎｔ ｕｎｄｅｒ ｔｈｅ ｓｅｃ⁃ ｏｎｄ⁃ｏｒｄｅｒ ｎｅｉｇｈｂｏｒｓ ｐｒｏｔｏｃｏｌ 通过对图 １ 和图 ２ 进行比较分析，我们发现多 智能体系统（１）在二阶邻居协议（３）下的收敛性更 好，即在二阶邻居协议（３）下各智能体达到一致性 的速度要比在一阶邻居协议（２） 下更快。 因此，在 设计多智能体系统时，尽可能地选用基于二阶邻居 的一致性协议，会使系统更快速地达到一致性。 为了控制多智能体系统（１） 的状态，我们把能 够获得外部控制输入的智能体称为领航者，其余的 智能体称为跟随者。 令 ＶＬ (Ｇ) 为领航者的集合， ＶＦ (Ｇ) ＝ Ｖ(Ｇ) － ＶＬ (Ｇ) 为跟随者的集合，则基于二 阶邻居的一致性协议（３）规则可以修改为 ｘ · ｉ (ｔ) ＝ － ∑ ｊ∈Ｎｉ ｘｉ (ｔ) － ｘｊ ( (ｔ) ) － ∑ｋ∈Ｎ２ ｉ ｘｉ (ｔ) － ｘｋ ( (ｔ) ) ， ｖｉ ∈ ＶＦ (Ｇ) ｘｉ (ｔ) ＝ ｕｉ， ｖｉ ∈ ＶＬ (Ｇ) ì î í ï ï ï ï ï ï （８） 式中： ｕｉ ＝ ｕｉ (ｔ) ∈ Ｒ 为外部控制输入，且 ｕ 及 ｕ · ｉ 都 是有界的，即 ∃ｕＬ ∈ Ｒ ，使得 ‖ｕｉ‖ ≤ ｕＬ ，‖ｕ · ｉ‖ ≤ ｕ · Ｌ ，∀ｉ ＝ ｉ ＝ １，２，…，ｎ （９） 当在系统中选取后几个节点为领航者时，我们 把前 ＮＦ (ＮＦ ≥ １) 个节点记为跟随者的个数，其余 的节点代表领航者的个数，记为 ＮＬ (ＮＬ ≥ １) 。 所 以在具有 Ｎ 个智能体的系统中， ＮＦ ＝ Ｎ － ＮＬ 。 根据 文献［２１］，合并图的拉普拉斯矩阵 Ｌｃ 可分块为 Ｌｃ ＝ － Ｆ ｒ ｒ Ｔ Ｂ é ë ê ê ù û ú ú 式中：矩阵 Ｆ ∈ Ｒ ＮＦ ×ＮＦ 代表跟随者之间的传递关系， 矩阵 Ｂ ∈ Ｒ ＮＬ ×ＮＬ 代表领航者之间的传递关系，矩阵 ｒ ∈Ｒ ＮＦ ×ＮＬ 代表领航者和跟随者之间的传递关系。 当在系统中选取任意多个节点为领航者时，假 设系统中有 ＮＬ 个领航者，我们规定矩阵 ｒ 取自矩阵 Ｌｃ 中这 ＮＬ 个节点所在的列向量减去这 ＮＬ 个节点所 在行向量和列向量的共同元素后剩余元素所组成的 ＮＦ × ＮＬ 矩阵。 矩阵 － Ｆ 为合并图拉普拉斯矩阵 Ｌｃ 减去这 ＮＬ 个节点所在行和所在列后剩下的 ＮＦ × ＮＦ 矩阵。 ３ 实例分析 对于一个具有 ５ 个节点的拓扑图，我们取第 ２ 个和第 ４ 个节点作为领航者，如图 ３。 图 ３ 具有 ５ 个节点的拓扑图 Ｆｉｇ．３ Ｔｏｐｏｌｏｇｙ ｗｉｔｈ ５ ｎｏｄｅｓ 那么 Ｌ ＝ Ｄ － Ａ ＝ １ － １ ０ ０ ０ － １ ２ － １ ０ ０ ０ － １ ２ － １ ０ ０ ０ － １ ２ － １ ０ ０ ０ － １ １ é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú Ｌ ～ ＝ Ｄ ～ － Ａ ～ ＝ １ ０ － １ ０ ０ ０ １ ０ － １ ０ － １ ０ ２ ０ － １ ０ － １ ０ １ ０ ０ ０ － １ ０ １ é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú 所以 Ｌｃ ＝ Ｌ ＋ Ｌ ～ ＝ ２ － １ － １ ０ ０ － １ ３ － １ － １ ０ － １ － １ ４ － １ － １ ０ － １ － １ ３ － １ ０ ０ － １ － １ ２ é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú 假设领航者能够获得输出向量 ｙ ， 且 ｙ ∈ Ｒ ＮＬ ×１ ，那么，网络系统的动态方程可以写为文献 ［９］所描述的那样： ·２１６· 智 能 系 统 学 报 第 １２ 卷

第2期 王康，等：二阶邻居协议下多智能体系统能控能观性保持 ·217. 4.1 g =Fxg ru 结构能控性 (10) 定义1对于一个无权重的多智能体系统，如 ly=rxp 果能够找到至少一组权重，使得相应的系统变为能 定理2若合并图的拉普拉斯矩阵L.的子矩阵 控，那么称这个多智能体系统是结构能控的。 F所对应的正交特征向量组成的矩阵U不与向量r 在文章[18]中，可以知道多智能体系统是结构 正交，则此拓扑图所对应的多智能体系统既是能控 能控的，当且仅当系统的拓扑图是连通的，即代数连 的，又是能观测的。 通度入2>0。可以借助结构能控性的概念，通过给 证明根据式(10)，可得能控性判别矩阵： 拓扑图的边赋予相应的权值，使本来不能控的系统 C=[rFrF2r…Fm-lr] (11) 变为能控，以达到对多智能体系统的状态要求。 因为拉普拉斯矩阵L与立分别是对称矩阵，所 4.2实例分析 以L+也为对称矩阵。故子矩阵F是对称矩阵。 对于图4所示的简单图G,我们给边赋予一组 根据对称矩阵的性质可得F=UDU,其中D是以 权值，其中，实线表示实际图g的连结方式，虚线表 示虚拟图g。的连结方式，我们选择第4个节点作为 矩阵F的特征值为元素的对角矩阵，U是矩阵F的 领航者，那么：实际图的拉普拉斯矩阵L和虚拟图 正交特征向量组成的矩阵。所以能控性判别矩阵： 的拉普拉斯矩阵分别为 C=[r UDU'r (UDU)'r ..(UDU)r] 「2-2 0 07 可写为 -2 3 -1 -4 L= C=r UDU'r UD'U'r ..UD"-'Ur]= 0 -1 4 -3 -4 -3 7 U[U'r DU'r D'U'r ..D"-U'r] 「3 0 -2 -17 因为U是非奇异矩阵，若使能控性判别矩阵C 0 0 0 0 满秩，只需要保证矩阵 L= -20 2 0 U'r DU'r D'Ur ..D-Ur] -10 0 1 行满秩即可。又因为对角矩阵D是非奇异矩阵，所 所以基于二阶邻居协议下多智能体系统的拉普 以Ur≠0即可保证系统能控。能观性判别矩阵： 拉斯矩阵为 r -2 -2-1 rF -2 3 -4 0= (12) L,=L+L= -2 -1 -3 rFa-t -1-4-3 8 同理，若使能观性判别矩阵O满秩，则也需使 Ur≠0。也就是说，若多智能体系统是能控的，那 么它也是能观测的。证毕。 2 综上所述，在二阶邻居协议下，多智能体系统既 能控又能观测的条件为：矩阵F所对应的特征向量 3 U不与向量r正交。 图4权图 4对结构能控性维持策略的研究 Fig.4 Weight graph 由式(11)得，能控性判别矩阵为 在基于二阶邻居协议(3)下具有时变拓扑结构 「-191157 的多智能体系统(1)随时间变化过程中，各节点之 C= -4-23-167 间边的条数和距离可能发生变化，进而影响系统合 -3-12-67 并图的拉普拉斯矩阵L。,并根据定理2和文献 式中：rank(C)=3。所以，通过给边赋予权值后，网 [1],在某一时刻，可能也会导致代数连通度入，发 络系统具有能控性和能观测性。因此我们就称原系 生改变以及使得系统不能控。因此，为了避免具有 统是结构能控的。 时变拓扑结构的多智能体系统(1)的能控性发生改 根据结构能控性的定义和文献[18]，可得到图5 变，我们引入了结构能控性的概念

ｘ · Ｆ ＝ ＦｘＦ ＋ ｒｕ ｙ ＝ ｒ Ｔ ｘＦ { （１０） 定理 ２ 若合并图的拉普拉斯矩阵 Ｌｃ 的子矩阵 Ｆ 所对应的正交特征向量组成的矩阵 Ｕ 不与向量 ｒ 正交，则此拓扑图所对应的多智能体系统既是能控 的，又是能观测的。 证明 根据式（１０），可得能控性判别矩阵： Ｃ ＝ ｒ Ｆｒ Ｆ ２ ｒ … Ｆ ｎ－１ [ ｒ] （１１） 因为拉普拉斯矩阵 Ｌ 与 Ｌ ～ 分别是对称矩阵，所 以 Ｌ ＋ Ｌ ～ 也为对称矩阵。 故子矩阵 Ｆ 是对称矩阵。 根据对称矩阵的性质可得 Ｆ ＝ ＵＤ ＾ Ｕ Ｔ ，其中 Ｄ ＾ 是以 矩阵 Ｆ 的特征值为元素的对角矩阵， Ｕ 是矩阵 Ｆ 的 正交特征向量组成的矩阵。 所以能控性判别矩阵： Ｃ ＝ ｒ ＵＤ ＾ Ｕ Ｔ ｒ （ＵＤ ＾ Ｕ Ｔ ） ２ ｒ … （ＵＤ ＾ Ｕ Ｔ ） ｎ－１ [ ｒ] 可写为 Ｃ ＝ ｒ ＵＤ ＾ Ｕ Ｔ ｒ ＵＤ ＾ ２Ｕ Ｔ ｒ … ＵＤ ＾ ｎ－１Ｕ Ｔ [ ｒ] ＝ Ｕ Ｕ Ｔ ｒ Ｄ ＾ Ｕ Ｔ ｒ Ｄ ＾ ２Ｕ Ｔ ｒ … Ｄ ＾ ｎ－１Ｕ Ｔ [ ｒ] 因为 Ｕ 是非奇异矩阵，若使能控性判别矩阵 Ｃ 满秩，只需要保证矩阵 Ｕ Ｔ ｒ Ｄ ＾ Ｕ Ｔ ｒ Ｄ ＾ ２Ｕ Ｔ ｒ … Ｄ ＾ ｎ－１Ｕ Ｔ [ ｒ] 行满秩即可。 又因为对角矩阵 Ｄ ＾ 是非奇异矩阵，所 以 Ｕ Ｔ ｒ ≠ ０ 即可保证系统能控。 能观性判别矩阵： Ｏ ＝ ｒ Ｔ ｒ ＴＦ ︙ ｒ ＴＦ ｎ－１ é ë ê ê ê ê ê ù û ú ú ú ú ú ＝ Ｃ Ｔ （１２） 同理，若使能观性判别矩阵 Ｏ 满秩，则也需使 Ｕ Ｔ ｒ ≠ ０。 也就是说，若多智能体系统是能控的，那 么它也是能观测的。 证毕。 综上所述，在二阶邻居协议下，多智能体系统既 能控又能观测的条件为：矩阵 Ｆ 所对应的特征向量 Ｕ 不与向量 ｒ 正交。 ４ 对结构能控性维持策略的研究 在基于二阶邻居协议（３）下具有时变拓扑结构 的多智能体系统（１）随时间变化过程中，各节点之 间边的条数和距离可能发生变化，进而影响系统合 并图的拉普拉斯矩阵 Ｌｃ ，并根据定理 ２ 和文献 ［１］，在某一时刻，可能也会导致代数连通度 λ２ 发 生改变以及使得系统不能控。 因此，为了避免具有 时变拓扑结构的多智能体系统（１）的能控性发生改 变，我们引入了结构能控性的概念。 ４．１ 结构能控性 定义 １ 对于一个无权重的多智能体系统，如 果能够找到至少一组权重，使得相应的系统变为能 控，那么称这个多智能体系统是结构能控的。 在文章［１８］中，可以知道多智能体系统是结构 能控的，当且仅当系统的拓扑图是连通的，即代数连 通度 λ２ ＞ ０。 可以借助结构能控性的概念，通过给 拓扑图的边赋予相应的权值，使本来不能控的系统 变为能控，以达到对多智能体系统的状态要求。 ４．２ 实例分析 对于图 ４ 所示的简单图 Ｇ ，我们给边赋予一组 权值，其中，实线表示实际图 ｇ 的连结方式，虚线表 示虚拟图 ｇｖ 的连结方式，我们选择第 ４ 个节点作为 领航者，那么：实际图的拉普拉斯矩阵 Ｌ 和虚拟图 的拉普拉斯矩阵 Ｌ ～ 分别为 Ｌ ＝ ２ － ２ ０ ０ － ２ ３ － １ － ４ ０ － １ ４ － ３ ０ － ４ － ３ ７ é ë ê ê ê ê ê ù û ú ú ú ú ú Ｌ ～ ＝ ３ ０ － ２ － １ ０ ０ ０ ０ － ２ ０ ２ ０ － １ ０ ０ １ é ë ê ê ê ê ê ù û ú ú ú ú ú 所以基于二阶邻居协议下多智能体系统的拉普 拉斯矩阵为 Ｌｃ ＝ Ｌ ＋ Ｌ ～ ＝ ５ － ２ － ２ － １ － ２ ３ － １ － ４ － ２ － １ ６ － ３ － １ － ４ － ３ ８ é ë ê ê ê ê ê ù û ú ú ú ú ú 图 ４ 权图 Ｆｉｇ．４ Ｗｅｉｇｈｔ ｇｒａｐｈ 由式（１１）得，能控性判别矩阵为 Ｃ ＝ － １ ９ １１５ － ４ － ２３ － １６７ － ３ － １２ － ６７ é ë ê ê ê ù û ú ú ú 式中： ｒａｎｋ(Ｃ) ＝ ３。 所以，通过给边赋予权值后，网 络系统具有能控性和能观测性。 因此我们就称原系 统是结构能控的。 根据结构能控性的定义和文献［１８］，可得到图 ５ 第 ２ 期 王康，等： 二阶邻居协议下多智能体系统能控能观性保持 ·２１７·