【机器学习】基于极大熵的知识迁移模糊聚类算法

第12卷第1期 智能系统学报 Vol.12 No.1 2017年2月 CAAI Transactions on Intelligent Systems Feb.2017 D0I:10.11992/tis.201602003 网络出版地址：http:/kns.cmki.net/kcms/detail/23.1538.TP.20170227.1758.006.html 基于极大熵的知识迁移模糊聚类算法 陈爱国2，王士同 (1.江南大学数字媒体学院，江苏无锡214122：2.香港理工大学计算机系，香港九龙999077) 摘要：针对传统的聚类算法在样本数据量不足或样本受到污染情况下的聚类性能下降问题，在经典的极大嫡聚类 算法(MEKT℉CA)的基础上，提出了一种新的融合历史聚类中心点和历史隶属度这两种知识的基于极大嫡的知识迁 移模糊聚类算法。该算法通过学习由源域总结出来的有益历史聚类中心和历史隶属度知识来指导数据量不足或受 污染的目标域数据的聚类任务，从而提高了聚类性能。通过一组模拟数据集和两组真实数据集构造的迁移场景上 的实验，证明了该算法的有效性。 关键词：知识迁移：极大嫡：聚类算法：极大嫡聚类：模糊聚类 中图分类号：TP274文献标志码：A文章编号：1673-4785(2017)12-0095-09 中文引用格式：陈爱国，王士同.基于极大熵的知识迁移模糊聚类算法[J].智能系统学报，2017,12(1)：95-103. 英文引用格式：CHEN Aiguo,WANG Shitong..A maximum entropy-based knowledge transfer fuzzy clustering algorithm[J].CAAI transactions on intelligent systems,2017,12(1):95-103. A maximum entropy-based knowledge transfer fuzzy clustering algorithm CHEN Aiguo'2,WANG Shitong' (1.School of Digital Media,Jiangnan University,Wuxi 214122,China;2.Department of Computing,Hong Kong Polytechnic University,Kowloon 999077,China) Abstract:To address the issue of clustering performance degradation when traditional clustering algorithms are applied to insufficient and/or noisy data,a maximum entropy-based knowledge transfer fuzzy clustering algorithm is proposed.This improves the classical maximum entropy clustering algorithm for target domains by leveraging two kinds of knowledge from the source domain,i.e.,historical clustering centers and historical degree of membership, into the objective function proposed for clustering insufficient and/or noisy target data.The effectiveness of the proposed algorithm is demonstrated by experiments on several synthetic and two real datasets. Keywords:knowledge transfer;maximum entropy;clustering algorithms;maximum entropy clustering; fuzzy clustering 聚类是一种常用的数据分析方法，在人工智 法[4刃、基于层次的聚类算法[8-]、基于密度的聚类 能、模式识别和机器学习等领域1-)一直受到广泛 算法[0-)、基于图论的聚类算法]等。这些聚类 关注。聚类作为一种无监督的数据分析技术，通过 算法在针对特定的数据集进行聚类时，通常能获得 数据之间的疏密程度，将数据划分到不同的数据簇 理想的聚类效果。但这些聚类性能的有效获得都 中，使得簇内的数据之间关系比较紧密，而簇之间 离不开一个必要前提，那就是进行聚类时的数据必 的数据关系比较疏远。根据聚类使用方法的不同， 须是充分的，换句话说，这些聚类算法不适合处理 将聚类分成常见的一些类别：基于划分的聚类算 数据不充分的情况。 但在实际生产、生活中，数据不充分的情况或 收稿日期：2016-02-04.网络出版日期：2017-02-27. 数据受到污染的情况往往普遍存在。例如，在一个 基金项目：国家自然科学基金项目(61272210)：江苏省自然科学基 金项目(BK20130155). 新领域收集数据之初，数据往往是不充足的。又或 通信作者：陈爱国.E-mail:agchen@jiangnan.cdu.cn 者由于受到硬件设备的不稳定性或环境等一些因

第 １２ 卷第 １ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．１ ２０１７ 年 ２ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｆｅｂ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６０２００３ 网络出版地址：ｈｔｔｐ： ／ ／ ｋｎｓ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ＴＰ．２０１７０２２７．１７５８．００６．ｈｔｍｌ 基于极大熵的知识迁移模糊聚类算法 陈爱国１，２ ，王士同１ （１．江南大学 数字媒体学院，江苏 无锡 ２１４１２２； ２．香港理工大学 计算机系，香港 九龙 ９９９０７７） 摘 要：针对传统的聚类算法在样本数据量不足或样本受到污染情况下的聚类性能下降问题，在经典的极大熵聚类 算法（ＭＥＫＴＦＣＡ）的基础上，提出了一种新的融合历史聚类中心点和历史隶属度这两种知识的基于极大熵的知识迁 移模糊聚类算法。 该算法通过学习由源域总结出来的有益历史聚类中心和历史隶属度知识来指导数据量不足或受 污染的目标域数据的聚类任务，从而提高了聚类性能。 通过一组模拟数据集和两组真实数据集构造的迁移场景上 的实验，证明了该算法的有效性。 关键词：知识迁移；极大熵；聚类算法；极大熵聚类；模糊聚类 中图分类号：ＴＰ２７４ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）１２－００９５－０９ 中文引用格式：陈爱国，王士同．基于极大熵的知识迁移模糊聚类算法［Ｊ］． 智能系统学报， ２０１７， １２（１）： ９５－１０３． 英文引用格式：ＣＨＥＮ Ａｉｇｕｏ，ＷＡＮＧ Ｓｈｉｔｏｎｇ． Ａ ｍａｘｉｍｕｍ ｅｎｔｒｏｐｙ⁃ｂａｓｅｄ ｋｎｏｗｌｅｄｇｅ ｔｒａｎｓｆｅｒ ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（１）： ９５－１０３． Ａ ｍａｘｉｍｕｍ ｅｎｔｒｏｐｙ⁃ｂａｓｅｄ ｋｎｏｗｌｅｄｇｅ ｔｒａｎｓｆｅｒ ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ＣＨＥＮ Ａｉｇｕｏ １，２ ， ＷＡＮＧ Ｓｈｉｔｏｎｇ １ （１． Ｓｃｈｏｏｌ ｏｆ Ｄｉｇｉｔａｌ Ｍｅｄｉａ， Ｊｉａｎｇｎａｎ Ｕｎｉｖｅｒｓｉｔｙ， Ｗｕｘｉ ２１４１２２， Ｃｈｉｎａ； ２． Ｄｅｐａｒｔｍｅｎｔ ｏｆ Ｃｏｍｐｕｔｉｎｇ， Ｈｏｎｇ Ｋｏｎｇ Ｐｏｌｙｔｅｃｈｎｉｃ Ｕｎｉｖｅｒｓｉｔｙ， Ｋｏｗｌｏｏｎ ９９９０７７，Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｔｏ ａｄｄｒｅｓｓ ｔｈｅ ｉｓｓｕｅ ｏｆ ｃｌｕｓｔｅｒｉｎｇ ｐｅｒｆｏｒｍａｎｃｅ ｄｅｇｒａｄａｔｉｏｎ ｗｈｅｎ ｔｒａｄｉｔｉｏｎａｌ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍｓ ａｒｅ ａｐｐｌｉｅｄ ｔｏ ｉｎｓｕｆｆｉｃｉｅｎｔ ａｎｄ ／ ｏｒ ｎｏｉｓｙ ｄａｔａ， ａ ｍａｘｉｍｕｍ ｅｎｔｒｏｐｙ⁃ｂａｓｅｄ ｋｎｏｗｌｅｄｇｅ ｔｒａｎｓｆｅｒ ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｉｓ ｐｒｏｐｏｓｅｄ． Ｔｈｉｓ ｉｍｐｒｏｖｅｓ ｔｈｅ ｃｌａｓｓｉｃａｌ ｍａｘｉｍｕｍ ｅｎｔｒｏｐｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｔａｒｇｅｔ ｄｏｍａｉｎｓ ｂｙ ｌｅｖｅｒａｇｉｎｇ ｔｗｏ ｋｉｎｄｓ ｏｆ ｋｎｏｗｌｅｄｇｅ ｆｒｏｍ ｔｈｅ ｓｏｕｒｃｅ ｄｏｍａｉｎ， ｉ．ｅ．， ｈｉｓｔｏｒｉｃａｌ ｃｌｕｓｔｅｒｉｎｇ ｃｅｎｔｅｒｓ ａｎｄ ｈｉｓｔｏｒｉｃａｌ ｄｅｇｒｅｅ ｏｆ ｍｅｍｂｅｒｓｈｉｐ， ｉｎｔｏ ｔｈｅ ｏｂｊｅｃｔｉｖｅ ｆｕｎｃｔｉｏｎ ｐｒｏｐｏｓｅｄ ｆｏｒ ｃｌｕｓｔｅｒｉｎｇ ｉｎｓｕｆｆｉｃｉｅｎｔ ａｎｄ ／ ｏｒ ｎｏｉｓｙ ｔａｒｇｅｔ ｄａｔａ． Ｔｈｅ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ｔｈｅ ｐｒｏｐｏｓｅｄ ａｌｇｏｒｉｔｈｍ ｉｓ ｄｅｍｏｎｓｔｒａｔｅｄ ｂｙ ｅｘｐｅｒｉｍｅｎｔｓ ｏｎ ｓｅｖｅｒａｌ ｓｙｎｔｈｅｔｉｃ ａｎｄ ｔｗｏ ｒｅａｌ ｄａｔａｓｅｔｓ． Ｋｅｙｗｏｒｄｓ： ｋｎｏｗｌｅｄｇｅ ｔｒａｎｓｆｅｒ； ｍａｘｉｍｕｍ ｅｎｔｒｏｐｙ； ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍｓ； ｍａｘｉｍｕｍ ｅｎｔｒｏｐｙ ｃｌｕｓｔｅｒｉｎｇ； ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ 收稿日期：２０１６－０２－ ． 网络出版日期 基金项目：国家自然科 ０４ 学基金项目（６１２７２２ 聚类是一种常用的数据分 通信作者：陈爱国． Ｅ⁃ｍａｉｌ：ａｇｃｈｅｎ＠ ｊｉａｎｇｎａｎ．ｅｄｕ．ｃｎ ：２ １ ０ ０ １ ） ７ ； －０２－２７． ． 析方法，在人工智 能、模式识别和机器学习等领域［１－３］ 一直受到广泛 关注。 聚类作为一种无监督的数据分析技术，通过 数据之间的疏密程度，将数据划分到不同的数据簇 中，使得簇内的数据之间关系比较紧密，而簇之间 的数据关系比较疏远。 根据聚类使用方法的不同， 将聚类分成常见的一些类别：基于划分的聚类算 法［４－７］ 、基于层次的聚类算法［８－９］ 、基于密度的聚类 算法［１０－１１］ 、基于图论的聚类算法［１２］ 等。 这些聚类 算法在针对特定的数据集进行聚类时，通常能获得 理想的聚类效果。 但这些聚类性能的有效获得都 离不开一个必要前提，那就是进行聚类时的数据必 须是充分的，换句话说，这些聚类算法不适合处理 数据不充分的情况。 但在实际生产、生活中，数据不充分的情况或 数据受到污染的情况往往普遍存在。 例如，在一个 新领域收集数据之初，数据往往是不充足的。 又或 者由于受到硬件设备的不稳定性或环境等一些因 江苏省自然科学基 金项目(BK20130155)

.96 智能系统学报 第12卷 素的影响，可能会采集到受噪声干扰的失真数据。 表示第i个样本点隶属于第j类的程度；‖x:-y,‖ 对于不充足的数据和受到污染的数据进行聚类分 表示第i个样本点与第j类中心点的距离：α是正则 析时，如果直接采用传统聚类方法，往往会造成聚 化系数，由u构成隶属度矩阵U∈Rxc,由y,构成中 类结果的不理想，甚至有时会出现聚类失效的结果。 心点矩阵V∈Rc。 如何有效解决数据量不足和数据受污染情况 采用拉格朗日条件极值优化方法解得式(1)的 下的数据聚类性能问题，是近年来研究工作者的方 最优聚类中心V和隶属度U的迭代公式为 向之一。其中，知识迁移]机制的引入是一种有效 手段。知识迁移机制是指将历史数据（也称为源 i=1 域)中提炼的有益知识应用到对当前数据（也称为 Vi= j=1,2,…,C (2) 目标域)聚类任务的指导，用于提高当前数据的聚 类结果。历史数据与当前数据之间既存在着联系， 也存在着明显的差别。目前，应用知识迁移机制来 i=1,2,…,N 提高聚类性能的代表性算法有：在多任务中使用共 享子空间进行聚类的LSSMTC算法[，、使用K均值 exp 组合方法的CombKM算法[4]、使用自学习迁移机制 j=1,2,…,C (3) 的STC聚类算法[1s]、使用特征和样本协同机制的 根据上述推导，总结出MECA算法的具体步骤 Co-clustering聚类算法[u6]及迁移谱聚类TSC算 如下： 法[)。这些基于知识迁移的聚类算法虽然提高了 输入数据集X,分类数C,正则化系数，最大 一定的聚类性能，但离实际应用还有一定差距，且 迭代次数T,终止阈值ε。 这些聚类算法在进行聚类任务时需要完整的历史 输出最优隶属度U和聚类中心V。 数据集，这在一些特殊场合，如保密需要，完整的历 1)初始化迭代计数器t=0,随机初始化隶属度 史数据是不可能获得的。所以，研究一种有隐私保 矩阵U(0)。 护的高效迁移聚类算法具有必要性和实用性。 2)根据式(2)和1)的隶属度矩阵U(t)获得新 本文在经典的MECA聚类算法的基础上，通过 的类中心V(t)。 对MECA算法的目标函数进行改造，使其具有学习 3)根据式(3)和2)获得的类中心V(t)计算得 历史知识的能力，进而提高算法在样本量不充分或 新的隶属度U(t+1)。 受到污染情况下聚类的性能。 4)当IU(t+1)-U(t)‖<e或者t>T时算法终 止，否则跳转到2)。 1经典极大熵聚类算法 通过观察MECA算法的具体步骤可以看出，原 在传统C均值聚类算法的基础上，通过引入具 始的MECA算法不具有知识迁移的能力。 有明确物理含义的嫡，产生出了具有简洁的数学表 MECA算法在数据量充足时，可以使用上述迭 达式和明确物理含义特点的极大嫡模糊聚类算法。 代过程获得有效的类中心和隶属度。但当样本量 极大嫡模糊聚类算法有很多种不同的表达形式，其 不充足或样本被污染的情况下，直接使用MECA算 中文献[6-7]给出的是经典的极大嫡模糊聚类算 法获得的聚类中心往往严重偏离实际聚类中心，甚 法，其具体表述如下。 至有时会出现聚类失效的情况。因此，在数据量不 假设样本空间X={x:lx:eR,i=1,2,…,N}, 足或数据受到污染情况下，研究有效的聚类算法， 其中，N表示样本点的个数，R是实数集，d表示样 具有必要性和实际价值。 本点的维数。该样本包含C(1<C<V)个不同的类 2 基于极大熵的知识迁移模糊聚类 别，则经典的极大熵聚类算法(MECA)的目标函数 可表示为 在知识迁移理论[]中，当源域数据和目标域数 ,n=立24,1-g+ 据既存在一定的相关性，同时又存在着明显的差异 时，可通过对源域有益知识的充分利用来指导目标 i=1i=1 i=1i=1 4ge[0,,∑4，=1,1≤i≤N 域任务更好地完成。本文尝试通过将数据量充分 (1) s11 的源域知识迁移至数据量不足或被污染的目标域 式中：x:表示第i个样本点；y表示第j类中心点；严 的聚类任务中，来提高目标域的聚类性能

素的影响，可能会采集到受噪声干扰的失真数据。 对于不充足的数据和受到污染的数据进行聚类分 析时，如果直接采用传统聚类方法，往往会造成聚 类结果的不理想，甚至有时会出现聚类失效的结果。 如何有效解决数据量不足和数据受污染情况 下的数据聚类性能问题，是近年来研究工作者的方 向之一。 其中，知识迁移［１３］机制的引入是一种有效 手段。 知识迁移机制是指将历史数据（也称为源 域）中提炼的有益知识应用到对当前数据（也称为 目标域）聚类任务的指导，用于提高当前数据的聚 类结果。 历史数据与当前数据之间既存在着联系， 也存在着明显的差别。 目前，应用知识迁移机制来 提高聚类性能的代表性算法有：在多任务中使用共 享子空间进行聚类的 ＬＳＳＭＴＣ 算法［１４］ 、使用 Ｋ 均值 组合方法的 ＣｏｍｂＫＭ 算法［１４］ 、使用自学习迁移机制 的 ＳＴＣ 聚类算法［１５］ 、使用特征和样本协同机制的 Ｃｏ⁃ｃｌｕｓｔｅｒｉｎｇ聚 类 算 法［１６］ 及 迁 移 谱 聚 类 ＴＳＣ 算 法［１７］ 。 这些基于知识迁移的聚类算法虽然提高了 一定的聚类性能，但离实际应用还有一定差距，且 这些聚类算法在进行聚类任务时需要完整的历史 数据集，这在一些特殊场合，如保密需要，完整的历 史数据是不可能获得的。 所以，研究一种有隐私保 护的高效迁移聚类算法具有必要性和实用性。 本文在经典的 ＭＥＣＡ 聚类算法的基础上，通过 对 ＭＥＣＡ 算法的目标函数进行改造，使其具有学习 历史知识的能力，进而提高算法在样本量不充分或 受到污染情况下聚类的性能。 １ 经典极大熵聚类算法 在传统 Ｃ 均值聚类算法的基础上，通过引入具 有明确物理含义的熵，产生出了具有简洁的数学表 达式和明确物理含义特点的极大熵模糊聚类算法。 极大熵模糊聚类算法有很多种不同的表达形式，其 中文献［６－ ７］ 给出的是经典的极大熵模糊聚类算 法，其具体表述如下。 假设样本空间 Ｘ ＝ ｘｉ ｜ ｘｉ∈Ｒ ｄ { ，ｉ ＝ １，２，…，Ｎ} ， 其中，Ｎ 表示样本点的个数，Ｒ 是实数集，ｄ 表示样 本点的维数。 该样本包含 Ｃ（１＜Ｃ＜Ｎ） 个不同的类 别，则经典的极大熵聚类算法（ＭＥＣＡ）的目标函数 可表示为 Ｊ(Ｕ，Ｖ) ＝ ∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μｉｊ ‖ ｘｉ － ｖｊ‖２ ＋ α∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μｉｊ ｌｎ μｉｊ， μｉｊ ∈ ［０，１］，∑ Ｃ ｊ ＝ １ μｉｊ ＝ １，１ ≤ ｉ ≤ Ｎ （１） 式中：ｘｉ 表示第 ｉ 个样本点；ｖｊ 表示第 ｊ 类中心点；μｉｊ 表示第 ｉ 个样本点隶属于第 ｊ 类的程度；‖ｘｉ －ｖｊ‖２ 表示第 ｉ 个样本点与第 ｊ 类中心点的距离；α 是正则 化系数，由 μｉｊ构成隶属度矩阵 Ｕ∈Ｒ Ｎ×Ｃ ，由ｖｊ 构成中 心点矩阵 Ｖ∈Ｒ ｄ×Ｃ 。 采用拉格朗日条件极值优化方法解得式（１）的 最优聚类中心 Ｖ 和隶属度 Ｕ 的迭代公式为 ｖｊ ＝ ∑ Ｎ ｉ ＝ １ μｉｊ ｘｉ ∑ Ｎ ｉ ＝ １ μｉｊ ， ｊ ＝ １，２，…，Ｃ （２） μｉｊ ＝ ｅｘｐ － ‖ ｘｉ － ｖｊ‖２ α æ è ç ö ø ÷ ∑ Ｃ ｋ ＝ １ ｅｘｐ － ‖ ｘｉ － ｖｋ‖２ α æ è ç ö ø ÷ ， ｉ ＝ １，２，…，Ｎ ｊ ＝ １，２，…，Ｃ （３） 根据上述推导，总结出 ＭＥＣＡ 算法的具体步骤 如下： 输入 数据集 Ｘ，分类数 Ｃ，正则化系数 α，最大 迭代次数 Ｔ，终止阈值 ε 。 输出 最优隶属度 Ｕ 和聚类中心 Ｖ。 １）初始化迭代计数器 ｔ ＝ ０，随机初始化隶属度 矩阵 Ｕ（０）。 ２）根据式（２）和 １）的隶属度矩阵Ｕ（ｔ）获得新 的类中心 Ｖ（ｔ）。 ３）根据式（３）和 ２）获得的类中心Ｖ（ｔ）计算得 新的隶属度 Ｕ（ｔ＋１）。 ４）当‖Ｕ（ｔ＋１）－Ｕ（ｔ）‖＜ε 或者 ｔ＞Ｔ 时算法终 止，否则跳转到 ２）。 通过观察 ＭＥＣＡ 算法的具体步骤可以看出，原 始的 ＭＥＣＡ 算法不具有知识迁移的能力。 ＭＥＣＡ 算法在数据量充足时，可以使用上述迭 代过程获得有效的类中心和隶属度。 但当样本量 不充足或样本被污染的情况下，直接使用 ＭＥＣＡ 算 法获得的聚类中心往往严重偏离实际聚类中心，甚 至有时会出现聚类失效的情况。 因此，在数据量不 足或数据受到污染情况下，研究有效的聚类算法， 具有必要性和实际价值。 ２ 基于极大熵的知识迁移模糊聚类 在知识迁移理论［１３］中，当源域数据和目标域数 据既存在一定的相关性，同时又存在着明显的差异 时，可通过对源域有益知识的充分利用来指导目标 域任务更好地完成。 本文尝试通过将数据量充分 的源域知识迁移至数据量不足或被污染的目标域 的聚类任务中，来提高目标域的聚类性能。 ·９６· 智 能 系 统 学 报 第 １２ 卷

第1期 陈爱国，等：基于极大嫡的知识迁移模糊聚类算法 .97. 为了实现源域知识到目标域迁移的目的，需要 可靠。当B→∞时，目标域的聚类中心点与源域的聚 解决3个核心问题： 类中心点需保持一致性程度大，此时说明源域的聚 1)迁移什么知识： 类中心点知识可靠性高。 2)如何迁移： 根据上述分析，针对经典MECA算法不具有知 3)什么时候迁移。 识迁移能力的不足，本文在MECA算法的基础上结 首先，解决源域到目标域迁移什么知识的问 合上述两个规则，提出基于极大嫡知识迁移模糊聚 题。在基于划分的聚类算法中，隶属度和聚类中心 类算法，即MEKTFCA算法。该算法的原理如图1。 点是对聚类结果具有决定性作用的两个因素。故 历史聚类中心 历史隶属度 本文选择隶属度和聚类中心点作为被迁移的知识。 f… 其次，需要解决如何才能实现将源域的隶属度 经典MECA算法 MEKTFCA算法 聚类结果 和聚类中心点知识迁移到目标域的聚类任务中的 问题。我们通过以下两个规则来实现。 1)隶属度重要程度受约束规则 该规则对应的公式为 源数据集 目标数据集 mi(x,U,V,i)=aΣ∑4与Ix-y2+ i=1j=1 图1 MEKTFCA算法原理图 (1-)∑∑‖x-y,2, Fig.1 Overall framework of MEKTFCA algorithm MEKTFCA算法首先对源数据集，通过经典的 入∈[0,1] (4) MECA算法获得历史聚类中心，然后根据目标数据 式中：x:表示目标域中第i个样本点；，表示目标域 集和所获得的历史聚类中心，通过再次使用经典的 中第j类中心点：拟，表示目标域中第i个样本点隶属 MECA算法获得历史隶属度，最后通过MEKTFCA 于第j类的程度：拉，为目标域中第i个样本点相对于 算法和历史聚类中心及历史隶属度获得最终的聚 源域中第j类中心点的历史隶属度：入为隶属度重 类结果。 要程度受约束规则的平衡因子。通过隶属度重要 融入了隶属度重要程度受约束规则和聚类中 程度受约束规则来调整性地学习源域迁移过来的 心点变化最小规则得到的MEKTFCA算法的具体目 历史隶属度知识。平衡因子入控制着源域的历史 标函数为 隶属度和目标域的隶属度对最终聚类结果的影响 Jexc(K,V,立，U,)=J,(X,U,V,)+ 程度。当入→1时，说明迁移的历史隶属度的可靠 程度差，目标域的聚类结果更多地受到目标域的隶 Jor:(V.v)+a C∑gng =1j=1 属度的影响。当入→0时，说明迁移的历史隶属度 具有很高的可借鉴性，目标域的聚类结果更多地受 4e[0,1:24,=1,i=1,2…,N(6) =1 到迁移历史隶属度的影响。 其中 2)聚类中心点变化最小规则 该规则的公式为 x.,v.0=宫2，-产： i=1j=1 min/,(V,)=BΣIy-,2, B≥0 (7) (5) (8) 式中：y代表目标域的第j类中心点，代表源域的 J,(V,)=B∑Iy-9I2 第j类的历史类中心点：B表示类中心点变化最小规 观察式(6)可以看出，MEKTFCA算法从本质上 则的平衡因子：C是聚类数目。该规则实现的是源 来说是由3部分组成。第1部分是融入了对历史隶 域聚类中心点知识的迁移。通过该规则的使用确 属度知识的学习的J,(X,U,V,0)项。通过该项 保：当目标函数产生最优化解时，目标域的聚类中 的引入可以使用历史隶属度知识对目标域的聚类 心点在一定程度上与源域的中心点保持一致，并通 任务进行指导。第2部分是融人了对历史类中心点 过平衡因子B来控制保持一致的程度。当B0时， 目标域的聚类中心点与源域的聚类中心点需保持 知识学习的Jk,(V,)项。通过该项的引入可以更 致性程度小，此时说明源域的聚类中心点知识不 有效地帮助目标域聚类任务的执行。第3部分是原

为了实现源域知识到目标域迁移的目的，需要 解决 ３ 个核心问题： １）迁移什么知识； ２）如何迁移； ３）什么时候迁移。 首先，解决源域到目标域迁移什么知识的问 题。 在基于划分的聚类算法中，隶属度和聚类中心 点是对聚类结果具有决定性作用的两个因素。 故 本文选择隶属度和聚类中心点作为被迁移的知识。 其次，需要解决如何才能实现将源域的隶属度 和聚类中心点知识迁移到目标域的聚类任务中的 问题。 我们通过以下两个规则来实现。 １）隶属度重要程度受约束规则 该规则对应的公式为 ｍｉｎＪＫＴ１ （Ｘ，Ｕ，Ｖ，Ｕ ＾ ） ＝ λ∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μｉｊ ‖ ｘｉ － ｖｊ‖２ ＋ （１ － λ）∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μ ＾ ｉｊ ‖ ｘｉ － ｖｊ‖２ ， λ ∈ ［０，１］ （４） 式中：ｘｉ 表示目标域中第 ｉ 个样本点；ｖｊ 表示目标域 中第 ｊ 类中心点；μｉｊ表示目标域中第 ｉ 个样本点隶属 于第 ｊ 类的程度；μ ＾ ｉｊ为目标域中第 ｉ 个样本点相对于 源域中第 ｊ 类中心点的历史隶属度；λ 为隶属度重 要程度受约束规则的平衡因子。 通过隶属度重要 程度受约束规则来调整性地学习源域迁移过来的 历史隶属度知识。 平衡因子 λ 控制着源域的历史 隶属度和目标域的隶属度对最终聚类结果的影响 程度。 当 λ→１ 时，说明迁移的历史隶属度的可靠 程度差，目标域的聚类结果更多地受到目标域的隶 属度的影响。 当 λ→０ 时，说明迁移的历史隶属度 具有很高的可借鉴性，目标域的聚类结果更多地受 到迁移历史隶属度的影响。 ２）聚类中心点变化最小规则 该规则的公式为 ｍｉｎＪＫＴ２ （Ｖ，Ｖ ＾ ） ＝ β∑ Ｃ ｊ ＝ １ ‖ ｖｊ － ｖ ＾ ｊ‖２ ， β ≥ ０ （５） 式中：ｖｊ 代表目标域的第 ｊ 类中心点，ｖ ＾ ｊ 代表源域的 第 ｊ 类的历史类中心点；β 表示类中心点变化最小规 则的平衡因子；Ｃ 是聚类数目。 该规则实现的是源 域聚类中心点知识的迁移。 通过该规则的使用确 保：当目标函数产生最优化解时，目标域的聚类中 心点在一定程度上与源域的中心点保持一致，并通 过平衡因子 β 来控制保持一致的程度。 当 β→０ 时， 目标域的聚类中心点与源域的聚类中心点需保持 一致性程度小，此时说明源域的聚类中心点知识不 可靠。 当 β→¥时，目标域的聚类中心点与源域的聚 类中心点需保持一致性程度大，此时说明源域的聚 类中心点知识可靠性高。 根据上述分析，针对经典 ＭＥＣＡ 算法不具有知 识迁移能力的不足，本文在 ＭＥＣＡ 算法的基础上结 合上述两个规则，提出基于极大熵知识迁移模糊聚 类算法，即 ＭＥＫＴＦＣＡ 算法。 该算法的原理如图 １。 图 １ ＭＥＫＴＦＣＡ 算法原理图 Ｆｉｇ．１ Ｏｖｅｒａｌｌ ｆｒａｍｅｗｏｒｋ ｏｆ ＭＥＫＴＦＣＡ ａｌｇｏｒｉｔｈｍ ＭＥＫＴＦＣＡ 算法首先对源数据集，通过经典的 ＭＥＣＡ 算法获得历史聚类中心，然后根据目标数据 集和所获得的历史聚类中心，通过再次使用经典的 ＭＥＣＡ 算法获得历史隶属度，最后通过 ＭＥＫＴＦＣＡ 算法和历史聚类中心及历史隶属度获得最终的聚 类结果。 融入了隶属度重要程度受约束规则和聚类中 心点变化最小规则得到的 ＭＥＫＴＦＣＡ 算法的具体目 标函数为 ＪＭＥＫＴＦＣＡ Ｘ，Ｖ，Ｖ ＾ ，Ｕ，Ｕ ＾ ( ) ＝ ＪＫＴ１ （Ｘ，Ｕ，Ｖ，Ｕ ＾ ） ＋ ＪＫＴ２ （Ｖ，Ｖ ＾ ） ＋ α∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μｉｊ ｌｎ μｉｊ， μｉｊ ∈ ［０，１］；∑ Ｃ ｊ ＝ １ μｉｊ ＝ １，∀ｉ ＝ １，２，…，Ｎ （６） 其中 ＪＫＴ１ （Ｘ，Ｕ，Ｖ，Ｕ ＾ ） ＝ λ∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μｉｊ ‖ ｘｉ － ｖｊ‖２ ＋ （１ － λ）∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μ ＾ ｉｊ ‖ ｘｉ － ｖｊ‖２ （７） ＪＫＴ２ （Ｖ，Ｖ ＾ ） ＝ β∑ Ｃ ｊ ＝ １ ‖ ｖｊ － ｖ ＾ ｊ‖２ （８） 观察式（６）可以看出，ＭＥＫＴＦＣＡ 算法从本质上 来说是由 ３ 部分组成。 第 １ 部分是融入了对历史隶 属度知识的学习的 ＪＫＴ１ （Ｘ，Ｕ，Ｖ，Ｕ ＾ ） 项。 通过该项 的引入可以使用历史隶属度知识对目标域的聚类 任务进行指导。 第 ２ 部分是融入了对历史类中心点 知识学习的 ＪＫＴ２ （Ｖ，Ｖ ＾ ） 项。 通过该项的引入可以更 有效地帮助目标域聚类任务的执行。 第 ３ 部分是原 第 １ 期 陈爱国，等：基于极大熵的知识迁移模糊聚类算法 ·９７·

·98 智能系统学报 第12卷 MECA算法的正则化嫡项。同时，根据式(6)~(8) 中心点的迭代公式，给出MEKTFCA算法的具体步 可以发现，当隶属度重要程度受约束规则的平衡因 骤如下。 子入=1而且聚类中心点变化最小规则的平衡因子 输入历史类中心点：，目标数据集X,分类数 B=0这种特殊情况时，MEKTFCA算法就退化为经典 C,平衡因子入、B,正则化系数α，最大迭代次数T, 的MECA算法。MEKTFCA算法的本质是，通过调 终止阈值e。 节平衡因子入和B的大小，来调整历史隶属度和历 输出最优隶属度U和聚类中心V。 史类中心点对当前聚类任务的影响，从而改善由于 1)根据式(3)计算历史隶属度g。 数据量不足和数据被污染情况下直接采用MECA 2)初始化迭代计数器t=0。 算法造成聚类结果不理想的情况。 3)根据式(14)计算得到新的聚类中心V(t)。 2.1参数求解 4)根据式(13)计算得到新的隶属度矩阵U(t+1)。 式(6)的参数求解问题，即为在有约束条件下 5)当IU(t+1)-U(t)‖<ε或者t>T时算法终 求解最优的参数使得目标函数值最小。与MECA 止，否则跳转到3)。 求最优解方法相同，我们采用拉格朗日乘子法进行 以上算法步骤同时回答了实现知识迁移中的 求解，首先构造拉格朗日函数表达式，即 第3个核心问题：什么时候迁移。通过算法步骤可 L=24,1-I2+ 以看到，在算法不断迭代过程中，隶属度和中心点 i=1=1 的迭代公式中使用到了历史隶属度知识和历史类 N ∑4gx-y2+a 中心点知识。从而在算法的迭代过程中实现了知 gln+ 识的迁移。 2I-+立(4，- (9) 3 -1 实验结果及分析 式中7：为Lagrange乘子。 3.1实验设置 根据业=0得 为验证本文所提MEKTFCA算法的有效性，将 构造一组模拟数据集和两组真实数据集作为实验 (10) 所使用的迁移场景。同时，选择6种相关算法作为 对比算法，对它们的聚类性能进行比较。这6种算 因为有约束条件 法为：在多任务中使用共享子空间进行聚类的 (11) LSSMTC算法[4)，使用K均值组合方法的CombKM =1 算法[4]，使用自学习迁移机制的STC聚类算法[s], 将式(10)代入式(11)可得 使用特征和样本协同机制的Co-clustering聚类算 a) exp(1) 12 法[I6,迁移谱聚类TSC算法[以及经典的MECA c 算法[6刀。 为了对聚类算法的结果进行客观比较，本文采 将式(12)代入式(10)可得隶属度的迭代公 用统一的NMI18](normalized mutual information)和 式为 RI(rand index)两种指标对实验结果进行评价。 NMI的计算公式为 (13) A‖x:- NMI= 根据 =0解得聚类中心点迭代公式为 a vi 三】 式中：N代表数据集的样本数目；V,代表聚类到p类 [如，+(1-A,]+B号 的样本数目；N,代表类标签为q的样本数目；N,,代 (14) [A4,+(1-AN2,1+B 表同时聚类到P类和类标签为q的样本数目。RI i=1 评价指标的计算公式为 2.2算法步骤 Noo +Ni RI 根据上述的推导过程所获得的隶属度和聚类 N(N-1)/2

ＭＥＣＡ 算法的正则化熵项。 同时，根据式（６） ～ （８） 可以发现，当隶属度重要程度受约束规则的平衡因 子 λ ＝ １ 而且聚类中心点变化最小规则的平衡因子 β ＝ ０ 这种特殊情况时，ＭＥＫＴＦＣＡ算法就退化为经典 的 ＭＥＣＡ 算法。 ＭＥＫＴＦＣＡ 算法的本质是，通过调 节平衡因子 λ 和 β 的大小，来调整历史隶属度和历 史类中心点对当前聚类任务的影响，从而改善由于 数据量不足和数据被污染情况下直接采用 ＭＥＣＡ 算法造成聚类结果不理想的情况。 ２．１ 参数求解 式（６）的参数求解问题，即为在有约束条件下 求解最优的参数使得目标函数值最小。 与 ＭＥＣＡ 求最优解方法相同，我们采用拉格朗日乘子法进行 求解，首先构造拉格朗日函数表达式，即 Ｌ ＝ λ∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μｉｊ ‖ ｘｉ － ｖｊ‖２ ＋ (１ － λ) ∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μ ＾ ｉｊ ‖ ｘｉ － ｖｊ‖２ ＋ α∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μｉｊ ｌｎ μｉｊ ＋ β∑ Ｃ ｊ ＝ １ ‖ ｖｊ － ｖ ＾ ｊ‖２ ＋ ∑ Ｎ ｉ ＝ １ ηｉ ∑ Ｃ ｊ ＝ １ μｉｊ ( － １) （９） 式中 ηｉ 为 Ｌａｇｒａｎｇｅ 乘子。 根据 ∂Ｌ ∂μｉｊ ＝ ０ 得 μｉｊ ＝ ｅｘｐ － １ － ηｉ ＋ λ ‖ ｘｉ － ｖｊ‖２ α æ è ç ö ø ÷ （１０） 因为有约束条件 ∑ Ｃ ｊ ＝ １ μｉｊ ＝ １ （１１） 将式（１０）代入式（１１）可得 ｅｘｐ － ηｉ α æ è ç ö ø ÷ ＝ ｅｘｐ(１) ∑ Ｃ ｋ ＝ １ ｅｘｐ － λ ‖ ｘｉ － ｖｋ‖２ α æ è ç ö ø ÷ （１２） 将式（ １２） 代入式（ １０） 可得隶属度的迭代公 式为 μｉｊ ＝ ｅｘｐ － λ ‖ ｘｉ － ｖｊ‖２ α æ è ç ö ø ÷ ∑ Ｃ ｋ ＝ １ ｅｘｐ － λ ‖ ｘｉ － ｖｋ‖２ α æ è ç ö ø ÷ （１３） 根据 ∂Ｌ ∂ ｖｊ ＝ ０ 解得聚类中心点迭代公式为 ｖｊ ＝ ∑ Ｎ ｉ ＝ １ ［λμｉｊ ＋ （１ － λ）μ ＾ ｉｊ］ ｘｉ ＋ β ｖ ＾ ｊ ∑ Ｎ ｉ ＝ １ λμｉｊ ＋ （１ － λ）μ ＾ ｉｊ [ ] ＋ β （１４） ２．２ 算法步骤 根据上述的推导过程所获得的隶属度和聚类 中心点的迭代公式，给出 ＭＥＫＴＦＣＡ 算法的具体步 骤如下。 输入 历史类中心点 ｖ ＾ ｊ ，目标数据集 Ｘ，分类数 Ｃ，平衡因子 λ、β，正则化系数 α，最大迭代次数 Ｔ， 终止阈值 ε。 输出 最优隶属度 Ｕ 和聚类中心 Ｖ。 １）根据式（３）计算历史隶属度 μ ＾ ｉｊ。 ２）初始化迭代计数器 ｔ ＝ ０。 ３）根据式（１４）计算得到新的聚类中心Ｖ（ｔ）。 ４）根据式（１３）计算得到新的隶属度矩阵 Ｕ（ｔ＋１）。 ５）当‖Ｕ（ｔ＋１）－Ｕ（ｔ）‖＜ε 或者 ｔ＞Ｔ 时算法终 止，否则跳转到 ３）。 以上算法步骤同时回答了实现知识迁移中的 第 ３ 个核心问题：什么时候迁移。 通过算法步骤可 以看到，在算法不断迭代过程中，隶属度和中心点 的迭代公式中使用到了历史隶属度知识和历史类 中心点知识。 从而在算法的迭代过程中实现了知 识的迁移。 ３ 实验结果及分析 ３．１ 实验设置 为验证本文所提 ＭＥＫＴＦＣＡ 算法的有效性，将 构造一组模拟数据集和两组真实数据集作为实验 所使用的迁移场景。 同时，选择 ６ 种相关算法作为 对比算法，对它们的聚类性能进行比较。 这 ６ 种算 法为：在 多 任 务 中 使 用 共 享 子 空 间 进 行 聚 类 的 ＬＳＳＭＴＣ 算法［１４］ ，使用 Ｋ 均值组合方法的 ＣｏｍｂＫＭ 算法［１４］ ，使用自学习迁移机制的 ＳＴＣ 聚类算法［１５］ ， 使用特征和样本协同机制的 Ｃｏ⁃ｃｌｕｓｔｅｒｉｎｇ 聚类算 法［１６］ ，迁移谱聚类 ＴＳＣ 算法［１７］ 以及经典的 ＭＥＣＡ 算法［６－７］ 。 为了对聚类算法的结果进行客观比较，本文采 用统一的 ＮＭＩ ［１８］ （ ｎｏｒｍａｌｉｚｅｄ ｍｕｔｕａｌ ｉｎｆｏｒｍａｔｉｏｎ） 和 ＲＩ ［１９］ （ ｒａｎｄ ｉｎｄｅｘ） 两种指标对实验结果进行评价。 ＮＭＩ 的计算公式为 ＮＭＩ ＝ ∑ ｃ ｐ ＝ １∑ ｃ ｑ ＝ １ Ｎｐ，ｑ ｌｏｇ Ｎ·Ｎｐ，ｑ Ｎｐ·Ｎｑ æ è ç ö ø ÷ ∑ ｃ ｐ ＝ １ Ｎｐ ｌｏｇ Ｎｐ Ｎ æ è ç ö ø ÷ é ë ê ê ù û ú ú· ∑ ｃ ｑ ＝ １ Ｎｑ ｌｏｇ Ｎｑ Ｎ æ è ç ö ø ÷ é ë ê ê ù û ú ú 式中：Ｎ 代表数据集的样本数目；Ｎｐ代表聚类到 ｐ 类 的样本数目；Ｎｑ代表类标签为 ｑ 的样本数目；Ｎｐ，ｑ代 表同时聚类到 ｐ 类和类标签为 ｑ 的样本数目。 ＲＩ 评价指标的计算公式为 ＲＩ ＝ Ｎ００ ＋ Ｎ１１ Ｎ（Ｎ － １） ／ ２ ·９８· 智 能 系 统 学 报 第 １２ 卷

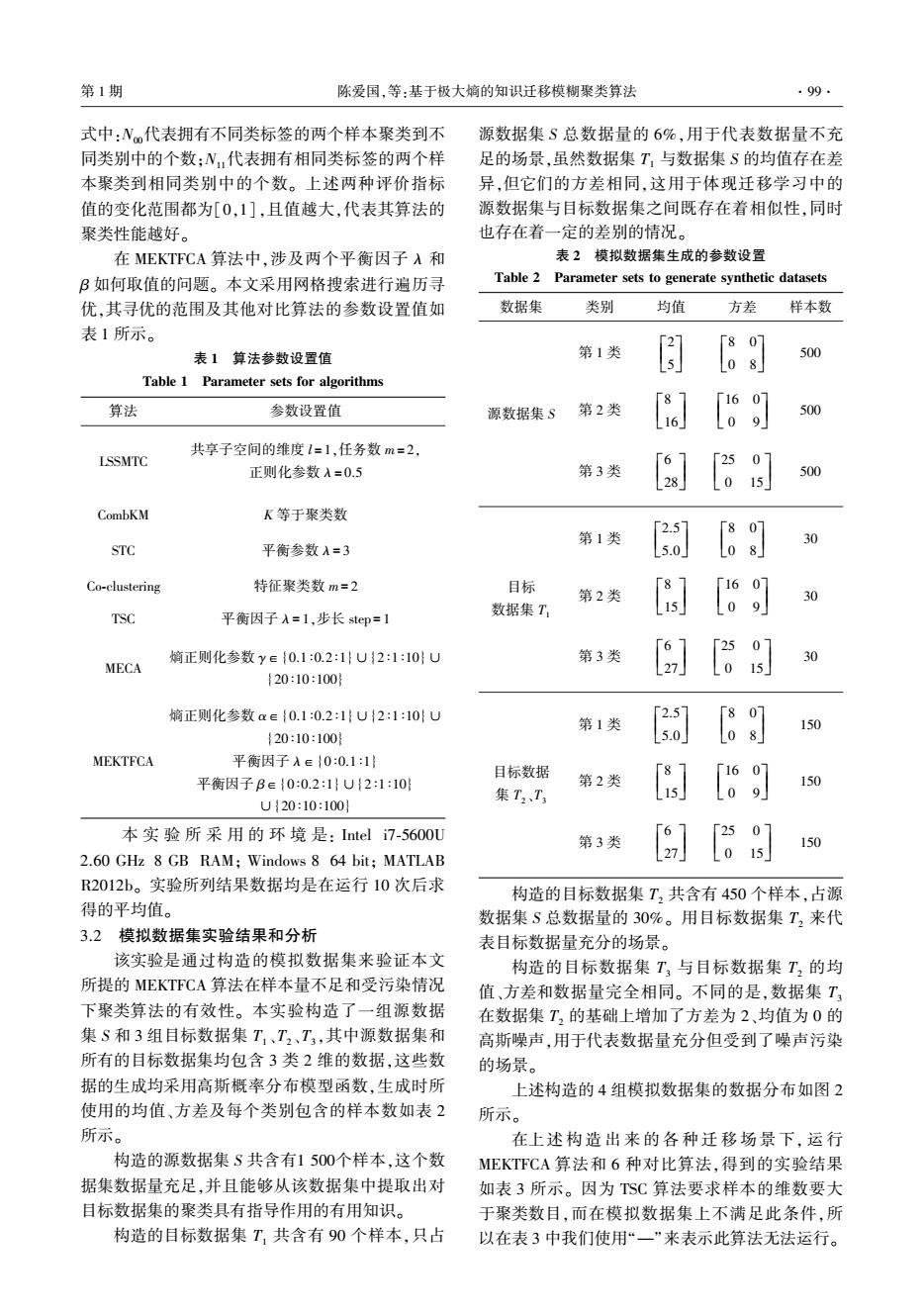
第1期 陈爱国，等：基于极大嫡的知识迁移模糊聚类算法 99. 式中：N代表拥有不同类标签的两个样本聚类到不 源数据集S总数据量的6%，用于代表数据量不充 同类别中的个数：N,代表拥有相同类标签的两个样 足的场景，虽然数据集T,与数据集S的均值存在差 本聚类到相同类别中的个数。上述两种评价指标 异，但它们的方差相同，这用于体现迁移学习中的 值的变化范围都为[0,1]，且值越大，代表其算法的 源数据集与目标数据集之间既存在着相似性，同时 聚类性能越好。 也存在着一定的差别的情况。 在MEKTFCA算法中，涉及两个平衡因子A和 表2模拟数据集生成的参数设置 B如何取值的问题。本文采用网格搜索进行遍历寻 Table 2 Parameter sets to generate synthetic datasets 优，其寻优的范围及其他对比算法的参数设置值如 数据集 类别 均值 方差 样本数 表1所示。 第1类 「2 「80 表1算法参数设置值 500 5 08 Table 1 Parameter sets for algorithms T8 [160 算法 参数设置值 源数据集S 第2类 16 09 500 共享子空间的维度l=1,任务数m=2. LSSMTC 正则化参数=0.5 第3类 [] [250 015 500 CombKM K等于聚类数 第1类 「2.57 「80] STC 平衡参数入=3 5.0 L08」 Co-clustering 特征聚类数m=2 目标 8 第2类 「160 30 TSC 平衡因子A=1,步长stp=1 数据集T 15 09 「25 第3类 0 熵正则化参数y∈{0.10.2：1}U{2:1:10}U 30 MECA 27 L015 {20:10:100} 嫡正则化参数a∈{0.1：0.2：1}U{2:1:10U 2.5 第1类 [80 150 {20:10:100} L5.0 08 MEKTFCA 平衡因子入∈{0：0.1：1} 目标数据 T8 「160 平衡因子B∈{0：0.2：11U{2:1:10 第2类 150 集T2、T3 15 09 U{20:10:100 本实验所采用的环境是：Intel i7-5600U 6 第3类 「2507 2.60 GHz 8 GB RAM;Windows 8 64 bit;MATLAB 27 L015 150 R2012b。实验所列结果数据均是在运行10次后求 构造的目标数据集T,共含有450个样本，占源 得的平均值。 数据集S总数据量的30%。用目标数据集T2来代 3.2模拟数据集实验结果和分析 表目标数据量充分的场景。 该实验是通过构造的模拟数据集来验证本文 构造的目标数据集T3与目标数据集T,的均 所提的MEKT℉CA算法在样本量不足和受污染情况 值、方差和数据量完全相同。不同的是，数据集T 下聚类算法的有效性。本实验构造了一组源数据 在数据集T2的基础上增加了方差为2、均值为0的 集S和3组目标数据集T1、T2、T,其中源数据集和 高斯噪声，用于代表数据量充分但受到了噪声污染 所有的目标数据集均包含3类2维的数据，这些数 的场景。 据的生成均采用高斯概率分布模型函数，生成时所 上述构造的4组模拟数据集的数据分布如图2 使用的均值、方差及每个类别包含的样本数如表2 所示。 所示。 在上述构造出来的各种迁移场景下，运行 构造的源数据集S共含有1500个样本，这个数 MEKTFCA算法和6种对比算法，得到的实验结果 据集数据量充足，并且能够从该数据集中提取出对 如表3所示。因为TSC算法要求样本的维数要大 目标数据集的聚类具有指导作用的有用知识。 于聚类数目，而在模拟数据集上不满足此条件，所 构造的目标数据集T1共含有90个样本，只占 以在表3中我们使用“一”来表示此算法无法运行

式中：Ｎ００代表拥有不同类标签的两个样本聚类到不 同类别中的个数；Ｎ１１代表拥有相同类标签的两个样 本聚类到相同类别中的个数。 上述两种评价指标 值的变化范围都为［０，１］，且值越大，代表其算法的 聚类性能越好。 在 ＭＥＫＴＦＣＡ 算法中，涉及两个平衡因子 λ 和 β 如何取值的问题。 本文采用网格搜索进行遍历寻 优，其寻优的范围及其他对比算法的参数设置值如 表 １ 所示。 表 １ 算法参数设置值 Ｔａｂｌｅ １ Ｐａｒａｍｅｔｅｒ ｓｅｔｓ ｆｏｒ ａｌｇｏｒｉｔｈｍｓ 算法 参数设置值 ＬＳＳＭＴＣ 共享子空间的维度 ｌ ＝ １，任务数 ｍ＝ ２， 正则化参数 λ＝ ０．５ ＣｏｍｂＫＭ Ｋ 等于聚类数 ＳＴＣ 平衡参数 λ＝ ３ Ｃｏ⁃ｃｌｕｓｔｅｒｉｎｇ 特征聚类数 ｍ＝ ２ ＴＳＣ 平衡因子 λ＝ １，步长 ｓｔｅｐ ＝ １ ＭＥＣＡ 熵正则化参数 γ∈｛０．１ ∶０．２ ∶１｝∪｛２ ∶１ ∶１０｝∪ ｛２０ ∶１０ ∶１００｝ ＭＥＫＴＦＣＡ 熵正则化参数 α∈｛０．１ ∶０．２ ∶１｝∪｛２ ∶１ ∶１０｝∪ ｛２０ ∶１０ ∶１００｝ 平衡因子 λ∈｛０ ∶０．１ ∶１｝ 平衡因子 β∈｛０ ∶０．２ ∶１｝∪｛２ ∶１ ∶１０｝ ∪｛２０ ∶１０ ∶１００｝ 本 实 验 所 采 用 的 环 境 是： Ｉｎｔｅｌ ｉ７⁃５６００Ｕ ２．６０ ＧＨｚ ８ ＧＢ ＲＡＭ； Ｗｉｎｄｏｗｓ ８ ６４ ｂｉｔ； ＭＡＴＬＡＢ Ｒ２０１２ｂ。 实验所列结果数据均是在运行 １０ 次后求 得的平均值。 ３．２ 模拟数据集实验结果和分析 该实验是通过构造的模拟数据集来验证本文 所提的 ＭＥＫＴＦＣＡ 算法在样本量不足和受污染情况 下聚类算法的有效性。 本实验构造了一组源数据 集 Ｓ 和 ３ 组目标数据集 Ｔ１ 、Ｔ２ 、Ｔ３ ，其中源数据集和 所有的目标数据集均包含 ３ 类 ２ 维的数据，这些数 据的生成均采用高斯概率分布模型函数，生成时所 使用的均值、方差及每个类别包含的样本数如表 ２ 所示。 构造的源数据集 Ｓ 共含有１ ５００个样本，这个数 据集数据量充足，并且能够从该数据集中提取出对 目标数据集的聚类具有指导作用的有用知识。 构造的目标数据集 Ｔ１ 共含有 ９０ 个样本，只占 源数据集 Ｓ 总数据量的 ６％，用于代表数据量不充 足的场景，虽然数据集 Ｔ１ 与数据集 Ｓ 的均值存在差 异，但它们的方差相同，这用于体现迁移学习中的 源数据集与目标数据集之间既存在着相似性，同时 也存在着一定的差别的情况。 表 ２ 模拟数据集生成的参数设置 Ｔａｂｌｅ ２ Ｐａｒａｍｅｔｅｒ ｓｅｔｓ ｔｏ ｇｅｎｅｒａｔｅ ｓｙｎｔｈｅｔｉｃ ｄａｔａｓｅｔｓ 数据集 类别 均值 方差 样本数 源数据集 Ｓ 第 １ 类 ２ ５ é ë êê ù û úú ８ ０ ０ ８ é ë êê ù û úú ５００ 第 ２ 类 ８ １６ é ë êê ù û úú １６ ０ ０ ９ é ë êê ù û úú ５００ 第 ３ 类 ６ ２８ é ë êê ù û úú ２５ ０ ０ １５ é ë êê ù û úú ５００ 目标 数据集 Ｔ１ 第 １ 类 ２．５ ５．０ é ë êê ù û úú ８ ０ ０ ８ é ë êê ù û úú ３０ 第 ２ 类 ８ １５ é ë êê ù û úú １６ ０ ０ ９ é ë êê ù û úú ３０ 第 ３ 类 ６ ２７ é ë êê ù û úú ２５ ０ ０ １５ é ë êê ù û úú ３０ 目标数据 集 Ｔ２ 、Ｔ３ 第 １ 类 ２．５ ５．０ é ë êê ù û úú ８ ０ ０ ８ é ë êê ù û úú １５０ 第 ２ 类 ８ １５ é ë êê ù û úú １６ ０ ０ ９ é ë êê ù û úú １５０ 第 ３ 类 ６ ２７ é ë êê ù û úú ２５ ０ ０ １５ é ë êê ù û úú １５０ 构造的目标数据集 Ｔ２ 共含有 ４５０ 个样本，占源 数据集 Ｓ 总数据量的 ３０％。 用目标数据集 Ｔ２ 来代 表目标数据量充分的场景。 构造的目标数据集 Ｔ３ 与目标数据集 Ｔ２ 的均 值、方差和数据量完全相同。 不同的是，数据集 Ｔ３ 在数据集 Ｔ２ 的基础上增加了方差为 ２、均值为 ０ 的 高斯噪声，用于代表数据量充分但受到了噪声污染 的场景。 上述构造的 ４ 组模拟数据集的数据分布如图 ２ 所示。 在上述 构 造 出 来 的 各 种 迁 移 场 景 下， 运 行 ＭＥＫＴＦＣＡ 算法和 ６ 种对比算法，得到的实验结果 如表 ３ 所示。 因为 ＴＳＣ 算法要求样本的维数要大 于聚类数目，而在模拟数据集上不满足此条件，所 以在表 ３ 中我们使用“—”来表示此算法无法运行。 第 １ 期 陈爱国，等：基于极大熵的知识迁移模糊聚类算法 ·９９·