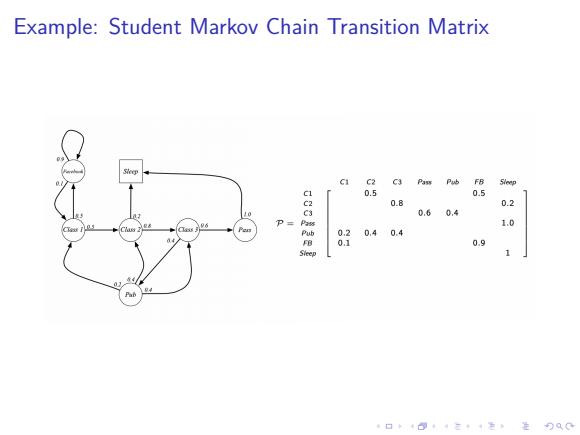
Example:Student Markov Chain Transition Matrix C1 C2 C3 Pass Pub FB 5 0.5 5 0.8 0.2 0.60,4 P= 1.0 870404 0.9 Sleep 口卡4三4色进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: Student Markov Chain Transition Matrix

Table of Contents 背景 基础 Markov Processes Markov Reward Process Markoy Decision Process Extensions to MDPs (Full Observable)Markov Decision Processes (MDPs) Partial Observable MDPs(POMDPs) 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Table of Contents 背景 基础 Markov Processes Markov Reward Process Markov Decision Process Extensions to MDPs (Full Observable) Markov Decision Processes (MDPs) Partial Observable MDPs (POMDPs)

Markov Reward Process A Markov reward process is a Markov chain with values. Definition A Markov Reward Process is a tuple (S,P,R,) S is a finite set of states p is a state transition probability matrix, Pss=P[St+1=s St=5] R is a reward function,Rs=E[Rt+1 S:=s] ■y is a discount factor,y∈0,l] 口卡4三4色进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Markov Reward Process
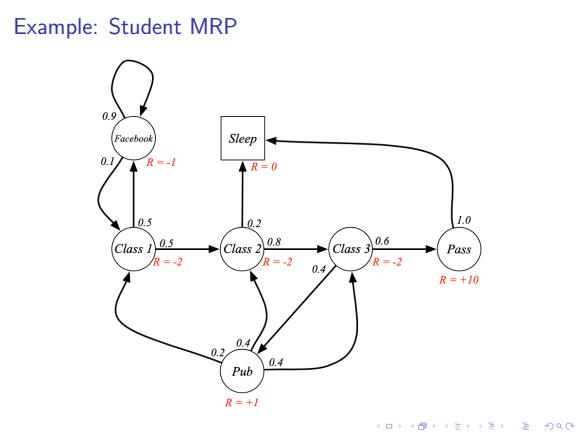
Example:Student MRP 0.9 Facebook Sleep 0.1 R=- ▲R=0 0.5 0.2 1.0 0.8 0.6 Class I Class 2 Class 3 Pass 2 R=-2 R=2 0.4 R=+10 0.4 0.2 0.4 Pub R=+/ 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: Student MRP

Return Definition The return Gt is the total discounted reward from time-step t. 00 G=R+1+yR+2+=∑YR+k+1 k=0 The discount yE [0,1]is the present value of future rewards The value of receiving reward R after k+1 time-steps is kR. This values immediate reward above delayed reward. yclose to 0 leads to"myopic"evaluation y close to 1 leads to "far-sighted"evaluation 口·三4,进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Return