
44 THEORY OF ELASTICITY TWO-DIMENSTONAL PROBLEMS 45 axis of a rectangular beam of unit width as(Q/2G),where Q is the ahenring force, evident that the first terms in the expressions for andr are the the corresponding inerease in curvature is given by the derivative of the above shearing strain with respect to z,which gives(/20G).The corrected expreasion values of the stresses calculated by the usual elementary formulas. for the eurvature by elementary analysis then becomes On the top end of the beam (x =0)the normal stress is zero.The shearing stress is 骨”+品=[2++小 w=一品e-州+品3。 tei5 e2(c-y) Comparing this with expression (35),it is seen that the elementary solution gives an exaggerated valuel for the correetion. Although these stresses are different from zero,they are very small all The correction term in expression (35)for the curvature cannot be attributed over the cross section and their resultant is zero,so that the condition to the ahearing foree alone.It is produced partially by the compressive stresses approaches that of an end free from external forces. These stresses are not uniformly distributed over the depth of the beam.The lateral expansion in the z-direction produced by these stresses diminishes from the By adding to o in Eqs.(@the term -gir,in which gi is the weight top to the bottom of the beam,and in this way a reversed curvuture (convex of unit volume of the material of the cantilever,the effect of the weight upwards)is produced.This curvature together with the effect of shearing force of the beam on the stress distribution is taken into account.It has accounts for the correetion term in Eg.(35). been proposed to use the solution obtained in this way for calculating 22.Other Cases of Continuously Loaded Beams.By increasing the stresses in masonry dams of rectangular cross section.It should the degree of polynomials representing solutions of the two-dimensional be noted that this solution does not satisfy the conditions at the bottom problem (Art.17),we may obtain solu- of the dam.Solution (a)is exact if,at the bottom,forces are acting tions of bending problems with various which are distributed in the same manner as e and rs in solution (a). types of continuously varying load.? In an actual case the bottom of the dam is connected with the founda- By taking,for instance,a solution in the tion,and the conditions are different from those represented by this form of a polynomial of the sixth degree solution.From Saint-Venant's principle it can be stated that the and combining it with the previous effect of the constraint at the bottom is negligible at large distances solutions of Art.17,we may obtain the from the bottom,but in the case of a masonry dam the cross-seetional stresses in a vertical cantilever loaded dimension 2c is usually not small in comparison with the height and by hydrostatic pressure,as shown in this effect cannot be neglected.* 1a.29 Fig.29.In this manner it can be By taking for the stress function a polynomial of the seventh degree shown that all conditions on the longitudinal sides of the cantilever are the stresses in a beam loaded by a parabolically distributed load may satisfied by the following system of stresses: be obtained. gg+(-2+号c) In the general case of a continuous distribution of load g,Fig.30,the stresses 9 at any cross section at a considerable distance from the ends,say at a distance larger than the depth of the beam,can be approximately caleulated from the ,=-+(结- following equations: (a) 1M.Levy,Compi.rend,vol.126,p.1235,1898. e-州-品e-州+最ce-州 3qx The problem of stresses in masonry dams is of great practical interest and has been diseussed by various authors.See K.Pearson,On Some Disregarded Points Here g is the weight of unit volume of the fluid,so that the intensity of in the Stability of Masonry Dams,Drapers'Co.Research Mems.,1904;K.Pearson and C.Pollard,An Experimental Study of the Stresses in Masonry Dams,Drapera' the load at a depth z is gx.The shearing force and the bending Co.Research Mems.,1907.See also papers by L.F.Richardson,Trans.Roy. moment at the same depth are gr/2 and ge"/6,respectively.It is Soc.(London)series A,vol.210,p.307,1910;and S.D.Carothers,Proc.Roy.Soc. A better approximation is given by clementary strain-energy considerations. Bdinburgh,vol.33,p.292,1913.I.Muller,Publications du laboratoire de photo- See S.Timoshenko,"Strength of Materials,"2d ed.,vol.1,p.299. Basticitd,Zirich,1930.Fillunger,Oesterr.Wochschr.affendl.Baudiene,1913, See papers by Timpe,loc.cit.:W.R.Ogood,J.Research Natl.Bur.Standards, Heft,45.K.Wolf,Siteber.Akad.Wiss.Wien,vol.123,1914. vol.28,p.159,1942. F.Seewald,Aihandl.aerodynam.Inst.,Tech.Hochschule,Aachen,vol.7,p.11; 1927

46 THEORY OF ELASTICITY TWO-DIMENSIONAL PROBLEMS 47 -9+(结-品) The general integral of this linear differential equation with constant coefficients is -昌+(g-) (36) f(y)-Ci cosh ay +Cs sinh ay Cay cosh ay +Cy sinh ay a-易e-四 The stress function then is in which 3f and Q are the bending moment -sin az(C:cosh cry Ca sinh ay +Cy cosh ay +Co sinh ay) (d) and sbearing forees ealeulated in the usual way and g is the intensity of lond at the and the corresponding stress components are cross section under consideration.These equations agree with those previously ob- .一g=曲Cco+cw3shay+Ca2 sinh ay tained for a uniformly loaded beam (see Art. ory cosh arg)+Ca(2 cosh ayay sinh av)] 21). If the lond of intensity g,in the down- )+o48000+和0+和g5090)zom80-= ward direction,is distributed along the lower 10.30. 8中 edge(y-十c)of the beam,the expressions 1ag一0z0y =-a cos az[Cia sinh ay +Cao cosh ary Ca(cosh ay for the stresses are obtained from Egs.(36)by superposing a uniform tensile streas, +ay sinh ay)+C(sinh ay ay cosh ay)] oy =g,and -9+(货-品) Let us consider a particular case of a reetangular benm supported at the ends and subjected along the upper and lower edges to the action of continuously ,昌+(能-) (387 m-员e-州 23.Solution of the Two-dimensional Problem in the Form of a Fourier Series. It haa been sbown that if the load is continuously distributed along the length of a rectangular beam of narrow cross section a stress function in the form of a poly- nomial may be used in certain simple cases.If the load is discontinuous,a stress funetion in the form of a trigonometric series should be used.1 The equation for the stress funetion, 1a.31. +3、0 中 +祭-0 (a) distributed vertical forces of the intensity A sin and B sin z,respectively. Figure 31 sbows the case when a=4/I and indicates also the positive values of may be satisfied by taking the function in the form A and B.The stress distribution for this ease can be obtained from solution (e) 中=m平e) ) The constants of integration C..,C.may be determined from the conditions on the upper and lower edges of the beam,y fc.These conditions are: Fory=十g in which mis an integer and f(y)a function of yonly.Substituting (b)into Eq.(a) tay =0,oy =-B gin az and using the notation m/,we find the following equation for determining 切 ): a)-2a"w)+fw())=0 (e) For y-c Tw=0, w■-A sin a 1The first application of trigonometric series in the solution of beam problems was given by M.C.Ribiere in a thesis,Sur divera cas de la flexion des prismea Substituting these valuea in the third of Ege.(e),we find rectangles,Bordeaux,1889.See also his paper in Compt.rend.,vol.126,pp.402- 404 and 1190-1192.Further progress in the applicntion of thia solution was made Caa ainh ac+Csa cosh ac +Ca(cosh ac cc sinh ac) by L.N.G.Filon,Phil.Trans.,series A,vol.201,p.63,1903.Several particular +Ca(sinh ce ac cosh ac)0 examples were worked out by F.Bleich,Bauingenieur,vol.4,p 255,1923. -'a snh ac+Cxa cosh ac Ca(cosh ac cc sinh ac) -Ca(sinh oc ec cosh cc)=0

TWO-DIMENSIONAL PROBLEMS 9 48 THEORY OF ELASTICITY For long beams ac,equal to mre/I,is small,provided the number of waves m is not from which large.Then,substituting in () a cosh ae Ca=-Ca cosh ae ac ainh ac a o sinh ac a-c+g+织+…; 2+ae)t cosh ac 1+foc)3 24+··· C--Ci sinh ae orc cosh oe and neglecting small quantities of higher order than (ee)",we find Usiag the conditions on the sides y tein the second of Eqs.(e),we find a*(Ci cosh ac C:sinh oc Cac cosh ac Cc sinh ac)=B 。=-A血a=(1-) a(Ci cosh oc -Cs sinh ac -Csc cosh ee Cac ginh cc)A By adding and subtracting these equations and using Egs.(g),we find Hence for small values of ac the distribution of stresses over the middle plane is praetically the same as on both hori- CB.sinh aeae cosh oe sontal edges (y te)of the beam.It ginh 2ac 2ac can be concluded that pressures are CaA-B.cosh ae+ae sinh ae transmitted through a beam or plate sinh 2ac -2oc () without any substantial change,pro- C,=4-B e cosh coc vided the variation of these pressures sinh 2cc -2ac along the sides is not rapid. C=-4+B a sinh ac The shearing stresses ry for this case a sinh 2ac 2oe are very amall.On the upper and Substituting in Egs.(e),we find the following expressions for the streas componenta: lower halves of the end cross seetions they add up to the small resultants (B)(ac cogh ae-sinh ae)cosh ayainh ay simh ae in necessary to balance the small differenee F10,32. sinh 20c 2ac between the pressures on the horizontal edges (y-te)and the middle plane (AB)ac sinh aecosh sinh ay ay coh ay cogh acin (g=0. sinh 2cc -2oe In the most general case the distribution of vertical loading along the upper (ac coth ae sinh a)cosh aay inh ay tinh ac.in and lower edges of a beam (Fig.32)can be represented by the following series:1 sinh 2ac 2ac ) For the upper edge, (AB)(ac sinh accoh a)anh y coh y cosh ae.si sinh 2ac -2oc g-4+An血+ A.cos m n=-4十)ohin之h ay smh,cos m】 sinh 2oc 2ac For the lower edge, (m) (AB)ae sinh ac cohry inh ay cosh aneco sinh 2ac -2ac g=B十 B平+∑Bo平 These stresses satisfy the conditions shown in Fig.31 along the sides y =c. At the ends of the beam z -0 and r =1,the stresses o are zero and only shearing stressis present.This stress is represented by two terms [sce Eqs.(k)].The The constant terms A.and Bo represent a uniform loading of the beam,which was first term,proportional to A+B,represents stresses which,for the upper and discussed in Art.21.Stresses produced by terma containing sin (mrr/)are lower halves of the end cross section,are of the same magnitude but of opposite obtained by aumming up solutions().The stresses produced by terms containing sign.The resultant of these stresses over the end is xero. The second term, cos (mx/)are easily obtained from (k)by exchanging sin az for cos er and vice proportional to A-B,has resultants at the ends of the beam which-maintain versa,and by changing the sign of av equilibrium with the loads applied to the longitudinal sides (y-+c). To illustrate the applieation of this general method of stress calculation in If these loads are the same for both sides,coefficient A is equal to B,and the reetangular plates,let us consider the case shown in Fig.33.For this ease of reactive forces at the ends vanish.Let us consider this particular case more in symmetrieal loading the terms with sin (mz/)vanish from expressions (m)and detail,assuming that the length of the beam is large in comparison with its depth. the coefficients A.and A.are obtnined in the usual manner; From the second of Eqs.(the normal stresses o over the middle plane y-0 For Fourier seriea see Osgood,"Advaneed Calculus,"1928;or Byerly,"Fourier of the beam are Series and Spberical Harmonics,"1902;or Churchill "Fourier Series and Bound- --2 oh e十na“hat ⑨ ary Value Probleme,"1941. sinh 2ee 2ac
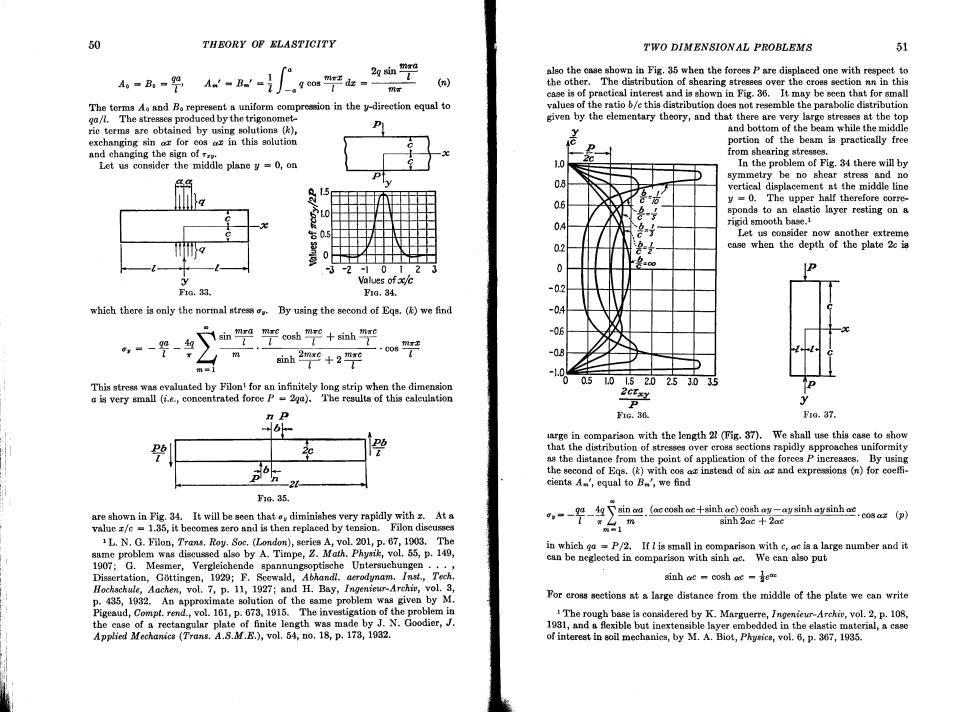
0 THEORY OP ELASTICITY TWO DIMENSIONAL PROBLEMS 51 a 2gn抛g also the case shown in Fig.35 when the forees P are displaced one with respect to A-B,-9 -B=平 (n) the other.The distribution of shearing atresses over the croes section nn in this case is of practieal interest and is sbown in Fig.36.It may be seen that for small The terms Ao and Bo represent a uniform compression in the y-direetion equal to values of the ratio b/e this distribution does not resemble the parabolic distribution ga/.The stresses produced by the trigonomet- given by the elementary theory,and that there are very large streascs at the top rie terms are obtained by using solutions () and bottom of the beam while the middle exchanging sin ar for eos a in this solution portion of the beam is practically free and changing the sign of r. from shearing stresscs. Let us consider the middle plane y =0,on 1.0 In the problem of Fig.34 there will by symmetry be no shear stress and no g 0.8 vertical displacement at the middle line 06 y =0.The upper half therefore corre- LO sponds to an elastic layer resting on a 04 rigid smooth base.1 Let us consider now another extreme 02 case when the depth of the plate 2c ia 3-2-101 2.o 2 Values of a/c F1G.33. F10.34. -02 which there is only the normal stress ou. By using the second of Eqs.(k)we find -0 -0E sin n平平cosh平+sinh inh2+2m ·cos mrz -08 This stress was evaluated by Filon!for an infinitely long strip when the dimension 0.5L01.520253035 a is very small (i.e.,concentrated foree P-2ga).The results of this calculation 2GFx这 n p 1G.3B Fra.37. arge in comparison with the length 21 (Fig.37).We shall use this case to show 2 that the distribution of stresses over cross sections rapidly approaches uniformity as the distance from the point of application of the forces P increascs.By using n the second of Egs.(k)with cos ar instead of sin az and expressions (n)for coeffi- -21 cients A",equal to B,we find F1G.35. are shown in Fig.34.It will be seen thato diminishes very rapidly with z.At a ,-g-_9∑血ag.(accosh+ainh )coh-aysinhaysinhac.co8atp) value r/e 1.35,it becomes sero and is then replaced by tension.Filon discusses sinh 2oc +2ac L.N.G.Filon,Trans.Roy.Soc.(London),series A,vol.201,p.67,1903.The in which ga P/2.If i is small in comparison with c,ac is a large number and it same problem was discussed also by A.Timpe,Z.Math.Physik,vol.55,p.149, can be neglected in comparison with sinh ec.We can also put 1907;G.Meamer,Vergleichende spannungsoptische Untersuehungen ... Dissertation,Gottingen,1929;F.Seewald,Abhandl.aerodynam.Inst.,Tech. ginh cc cosh ac teme Hochschule,Aachen,vol.7,p.11,1927;and H.Bay,Ingenieur-Archiv,vol.3, p.435,1932.An approximate solution of the same problem was given by M. For cross sections at a large distance from the middle of the plate we can write Pigeaud,Compt.rend.,vol.161,p.673,1915.The investigation of the problem in The rough base is considered by K.Marguerre,Ingenievr-Archiv,vol.2,p.108, the case of a rectangular plate of finite length was made by J.N.Goodier,J. 1931,and a flexible but inextensible layer embedded in the elastic material,a case Applied Mechanics (Trans.A.S.M.E.),vol.54,no.18,p.173,1932. of interest in soil mechanies,by M.A.Biot,Physics,vol.6,p.367,1935

TWO-DIMENSIONAL PROBLEMS 53 52 THEORY OF ELASTICITY sinh ay -cosh ay =Substituting these in Eq.(p),we find 24.Other Applieations of Fourier Series.Gravity Loading.The problems considered in Art.23 coneerned a single"span"or 21.The solutions,however, can equally well be regarded as representing periodie states of stress in long strips parallel to the z-axis,since a Fourier series represents a periodic function.A con- 2m tinuous beam consisting of a sequenee of equal spans similarly loaded will have such a periodie stress distribution if the end conditions are appropriate.If,as in certain reinforced-conerete bunker constructions,the beam is essentially a wall sin e-》+1e7 supportod at pointa whose distance apart is comparable with the depth (Fig.39), 2m useful resulta can be obtained by the present method.The elementary beam If e-yis not very small,say e-y>1/2,this series converges very rapidly and it is only necessary to take a few terms in calculating Then we can take 血-n2 and putting 2ag P,we find ,--,[学e-功+]0-学 2b D1G.39 For y -c-1,for instanee, theory is not adequate.A uniformly distributed load g on the lower edge,sup- ,-员-(o7+2击平++。 ported by upward reactions uniformly distributed in widths 2b at intervals 1 2 presents a special case covered by Eqs.(m)of Art.23.If the load gi is applied The first three terms of the series are sufficient to give good accuraey and the on the upper edge it is merely necessary to add the stress distribution due to equal stress distribution is as shown in Fig.386.In the same figure the stress distribu- and opposite uniformly distributed pressures gi on both upper and lower edges. tions for e-y=1/2 and c-y 21 are If the load is the weight of the beam itself the resulting body-foree problem may also given.1 It is evident that at a distanee at onee be reduced to an edge-load problem.The simple stress distribution (a) from the end equal to the width of the strip ==0,g=-时y十c,Tzw=0 the stress distribution is practically uniform, satisfics the equations of equilibrium and compatibility (19)and(24).It clearly c-y which confirms the conelusion usually made on the basis of Saint-Venant's principle. represents support by uniformly distributed pressure 2pgc on the lower edge in For a long strip such as in Fig.37 the a Fig.39.The condition that o is zero at the lower edge,exeept at the supporta stresses will be transmitted through the (of width 26),is satisfied by adding this stress distribution to that represented by width 2 of the plate with little change,pro- Fig.39 when g is replaeed by 2pgc,and the stress is due to g and g without body force. vided the rate of variation along the edge is Problems not too rapid.The stresses of the present c-yL solution will,however,require some correc- 1.Investigate what problem of plane stress is solved by the streas function tion on this account,especially near the ends, (c) y=te.A solution of the problem of Fig. -器(四-罰)+号r 2 37 with c21,by a different method, C-y24 yields a practically uniform compreasive 2.Investigate what problem is solved by P F10.38. stress over the middle horizontal section,in agreement with Fig.38c.The stresses in ,1中=-示列(3d-2圳 the vicinity of the points of application of the loads P will be discusaed later (see applied to the region included iny0,yd,-0,on the side z positive. page 85). Problems of this kind are discueed,with references,in the bookDie Statikim See paper by F.Bleich,loc.cit. Eisenbetonbau,"by K.Beyer,2ded,p.723,1934;see also H.Craemer,Ingenieur- J.N.Goodier,Trans.A.S.M.E.,voL.54,p.173,1932. 4rchi钟,vol.7,p.325,1938. INSTIIUTUL POLIE. TIMISOARA BIBLIOTECA CENTRALA