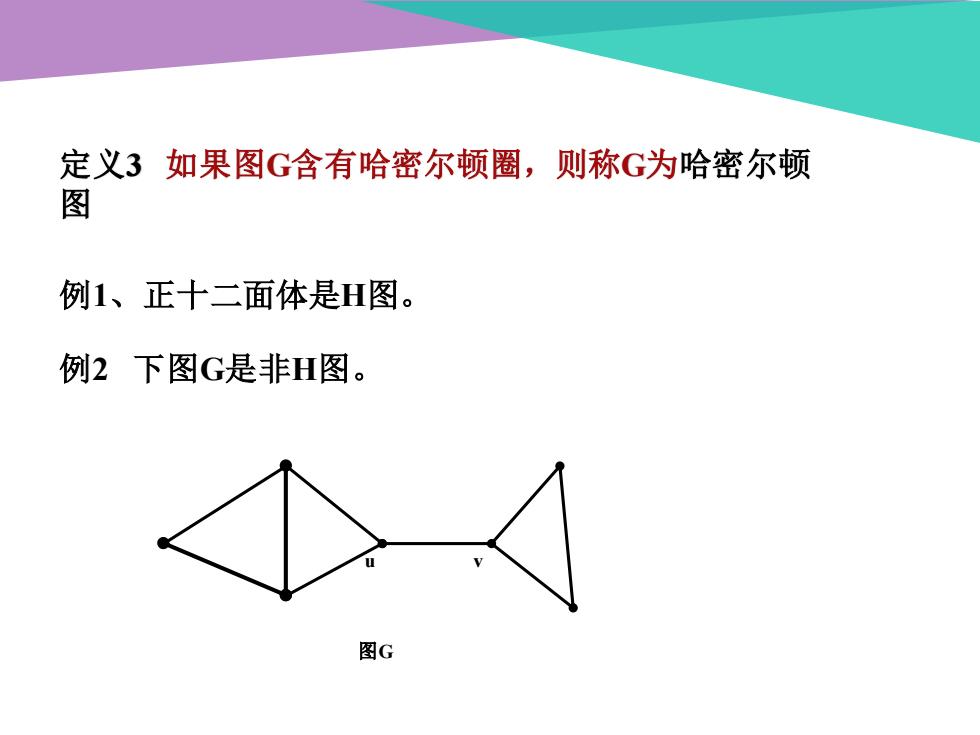
定义3如果图G含有哈密尔顿圈,则称G为哈密尔顿 图 例1、正十二面体是H图。 例2下图G是非H图。 图G
定义3 如果图G含有哈密尔顿圈,则称G为哈密尔顿 图 例1、正十二面体是H图。 例2 下图G是非H图。 图G u v

(二)、性质与判定 1、性质 定理1(必要条件) 若G为H图,则对V(G)的任一非空顶点子集S,有: o(G-S)≤1S 证明:设C是G的H圈,则对V(G)的任意非空子集S,容 易知道: o(C-S)≤|S o(G)表示 图G所含的连通分支的个数 所以,有: o(G-S)≤o(C-S)≤|S 7
(二)、性质与判定 1、性质 定理1 (必要条件) 若G为H图,则对V(G)的任一非空顶点子集S,有: ( ) G S S − 证明:设C是G的H圈,则对V(G)的任意非空子集S, 容 易知道: ( ) C S S − 所以,有: ( ) ( ) G S C S S − − 7 ω(G)表示 图G所含的连通分支的个数