安徽科技学院：《大学物理》课程教学资源（PPT课件）力学——第一章 质点运动学（Kinematics of Particles）

大学 物理 §1.2运动的描述(Description of Motion) l.位矢(position vector) —位矢 P(xy.2)F(t)=x(t)i+y(t)j+z(t)k 运动方程o运动函数 e.g.抛体运动： F(0=%i+(,t-g)万

§1.2运动的描述 (Description of Motion) 1.位矢 (position vector) O x z y r  • P(x,y,z) r  ——位矢 r t x t i y t j z t k     ( ) = ( ) + ( ) + ( ) ——运动方程 or 运动函数 e.g. 1 2 0 0 2 ( ) ( ) x y r t v ti v t gt j = + − 抛体运动： 7 大学 物理

大学 物理 2.位移(displacement) △S △产=F(t+△t)-(t) P2 一t至+△t内的位移 r(i r(t+△t) 国际单位制 .g.设)=i+tj+tk(S) 则在=0至1s内的位移 A=(①)-F(0)=j+km

2.位移 (displacement) r r(t t) r(t)     = +  − —— t 至 t+t 内的位移 ( ) ( ) 2 r t i t j t k SI     设 = + + 则在 t=0 至 1s 内的位移 r r(1) r(0)     = − j k m   = + x y z o r   S P1 r(t)  P2 r(t +  t)  e.g. 国际单位制 8 大学 物理

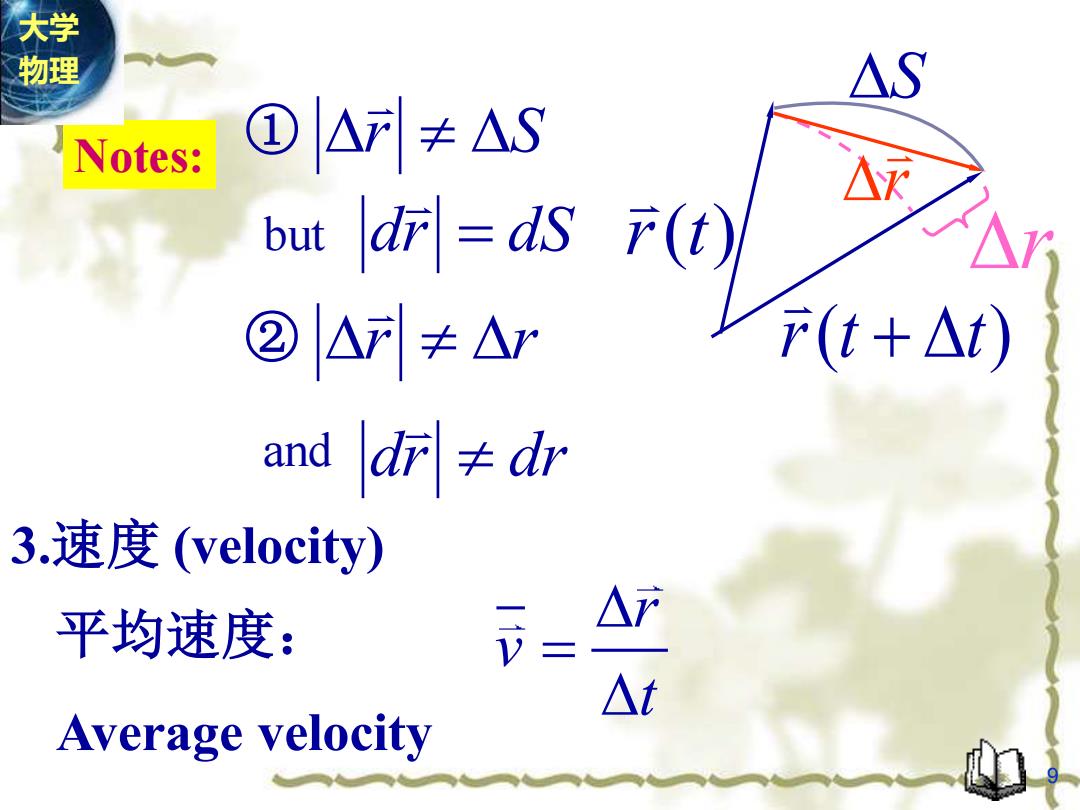
大学 物理 △S Notes: ①△列≠△S △ but d=ds F(t) ②△列≠△ F(t+△t) and |di≠dir 3.速度(velocity) 平均速度： △产 △t Average velocity

3.速度 (velocity) 平均速度 ： Average velocity r v t  =  ①  r   S  but dr = dS  r   r  ② and dr  dr  Notes:  r r  r( t )  r(t +  t )  S 9 大学 物理

大学 物理 瞬时速率： △产 d时 v= lim Instantaneous velocity: △t→0 △t dt Notes: ①平均速率：乊= △S △ △t △t ds dr 瞬时速率：v= dt dt = 2In curvilinear motion,the velocity vector is tangential to the curve

瞬时速率： Instantaneous velocity： 0 lim t r v t  →  =  dS v dt 瞬时速率： = ①平均速率： S v t  =  ②In curvilinear motion, the velocity vector is tangential to the curve. Notes: dr dt = r t    = v dr dt = = v 10 大学 物理

大学 一】 些速度值(m/s) 物理 真空中光速 ~3.0×108 太阳在银河系中的运动 ~3.0x105 地球的公转 ≈3.0×104 人造地球卫星 ~7.9x103 现代歼击机 ~9×102 空气中声速 ~3.3×102 猎豹 ≈2.8×10 载流导线中自由电子的漂移 ~104 大陆板块运动 ≈109

一些速度值(m/s) 真空中光速 ∼3.0108 太阳在银河系中的运动 ∼3.0105 地球的公转 ∼3.0104 人造地球卫星 ∼7.9103 现代歼击机 ∼9 102 空气中声速 ∼3.3102 猎豹 ∼2.8 10 载流导线中自由电子的漂移 ∼10– 4 大陆板块运动 ∼10– 9 11 大学 物理