
第12卷第3期 智能系统学报 Vol.12 No.3 2017年6月 CAAI Transactions on Intelligent Systems Jun.2017 D0I:10.11992/is.201605010 网络出版地址:http:/kns.cmki.ne/kcms/detail/23.1538.TP.20170705.1657.010.html REM记忆模型在图像分类识别中的应用 姜英,王延江 (中国石油大学信息与控制工程学院,山东青岛266580) 摘要:尝试将认知心理学中的记忆模型与图像学习识别联系在一起,研究基于REM(retrieving effective from memory)记忆模型的视觉图像存储与识别方法。采用方向梯度直方图(HOG)和局部二进模式(LBP)生成图像特征 向量,并对每个特征向量中的每一个分量按概率进行复制,允许错误复制,最后采用Bayesian决策计算被探测图像特 征向量与已学习图像集特征向量的平均似然比值,根据该值判断被探测图像是否已学习过。实验结果表明,提出的 算法不仅对同一个物体的小幅度旋转图像具有很好的识别效果,同时对同一类别物体图像识别也具有较好的效果, 而且其虚报率远远低于其他识别方法。 关键词:图像识别;i记忆建模;HOG特征;LBP特征;Bayesian决策 中图分类号:TP391文献标志码:A文章编号:1673-4785(2017)03-0310-08 中文引用格式:姜英,王延江.REM记忆模型在图像分类识别中的应用[J].智能系统学报,2017,12(3):310-317. 英文引用格式:JIANG Ying,WANG Yanjiang.Application of REM memory model in image recognition and classification[J]. CAAI transactions on intelligent systems,2017,12(3):310-317. Application of REM memory model in image recognition and classification JIANG Ying,WANG Yanjiang (College of Information and Control Engineering,China University of Petroleum,Qingdao 266580,China) Abstract:We attempt to combine a memory model with image learning and recognition and to research the application of the REM model in image recognition and classification.An image feature vector was obtained by histograms of oriented gradients (HOG)and local binary pattern (LBP)operators;every component of a feature vector was copied with a certain probability,allowing for an error-prone copy of the studied vector.Finally, Bayesian decision theory was applied for calculating the average likelihood ratio between the feature vector of the probe image and that of the studied image set.The value of the ratio was used to decide whether the probe image had been studied.Experimental results demonstrate that the proposed method can gain a good recognition effect not only for the classification of the same object with small rotation angles but also for the recognition of the same category object.Moreover,the false rate is far lower than that of other classification methods. Keywords:image recognition;memory modeling;HOG feature;LBP feature;Bayesian decision 视觉图像的分类与识别研究是计算机视觉研 网络分类器[3-),SVM支持向量机分类器s)、卷积神 究、模式识别与机器学习领域内的一个非常活跃的 经网络分类器[6)]、ELM极限学习机[]及稀疏编码方 方向,其在许多领域中应用广泛,如银行系统的人 法等。为获得良好的图像分类效果,研究者们在设 脸识别、防御系统的行人检测与跟踪、交通系统的 计图像分类方法及改进分类准确性方面都做了大 车牌检测与车辆跟踪等。近年来,图像分类山吸引 量工作。例如,稀疏编码方法已被证实在图像分类 了研究者们的注意,关于视觉图像识别与分类的各 中具有优秀的分类性能,基于该方法的许多改进的 种理论与算法层出不穷,如最近邻分类器】、神经 稀疏编码方法也被相继提出,如SRC方法[)、CRC 方法)、RSC方法[1o]及RLRC方法)等。尽管现 收稿日期:2016-05-13.网络出版日期:2017-07-05. 基金项目:国家自然科学基金项目(61271407,61301242):山东省自然 有的许多算法在图像分类方面表现突出,但目前已 科学基金项目(ZR2013FQ015):中央高校基本科研业务费专 有的识别分类算法大多侧重于“区别”,忽视了“认 项资金资助项目(14CX06066A). 通信作者:王延江.E-mail:yjwang@upc.sdu.cm 识”,即侧重将某一类物体与有限类已学过物体进
第 12 卷第 3 期 智 能 系 统 学 报 Vol.12 №.3 2017 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2017 DOI:10.11992 / tis.201605010 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170705.1657.010.html REM 记忆模型在图像分类识别中的应用 姜英,王延江 (中国石油大学 信息与控制工程学院,山东 青岛 266580) 摘 要:尝试将认知心理学中的记忆模型与图像学习识别联系在一起,研究基于 REM ( retrieving effective from memory)记忆模型的视觉图像存储与识别方法。 采用方向梯度直方图(HOG)和局部二进模式(LBP)生成图像特征 向量,并对每个特征向量中的每一个分量按概率进行复制,允许错误复制,最后采用 Bayesian 决策计算被探测图像特 征向量与已学习图像集特征向量的平均似然比值,根据该值判断被探测图像是否已学习过。 实验结果表明,提出的 算法不仅对同一个物体的小幅度旋转图像具有很好的识别效果,同时对同一类别物体图像识别也具有较好的效果, 而且其虚报率远远低于其他识别方法。 关键词:图像识别;记忆建模;HOG 特征;LBP 特征;Bayesian 决策 中图分类号:TP391 文献标志码:A 文章编号:1673-4785(2017)03-0310-08 中文引用格式:姜英, 王延江. REM 记忆模型在图像分类识别中的应用[J]. 智能系统学报, 2017, 12(3): 310-317. 英文引用格式:JIANG Ying, WANG Yanjiang. Application of REM memory model in image recognition and classification[ J]. CAAI transactions on intelligent systems, 2017, 12(3): 310-317. Application of REM memory model in image recognition and classification JIANG Ying,WANG Yanjiang (College of Information and Control Engineering, China University of Petroleum, Qingdao 266580, China) Abstract:We attempt to combine a memory model with image learning and recognition and to research the application of the REM model in image recognition and classification. An image feature vector was obtained by histograms of oriented gradients (HOG) and local binary pattern (LBP) operators; every component of a feature vector was copied with a certain probability, allowing for an error⁃prone copy of the studied vector. Finally, Bayesian decision theory was applied for calculating the average likelihood ratio between the feature vector of the probe image and that of the studied image set. The value of the ratio was used to decide whether the probe image had been studied.Experimental results demonstrate that the proposed method can gain a good recognition effect not only for the classification of the same object with small rotation angles but also for the recognition of the same category object. Moreover, the false rate is far lower than that of other classification methods. Keywords:image recognition; memory modeling; HOG feature; LBP feature; Bayesian decision 收稿日期:2016-05-13. 网络出版日期:2017-07-05. 基金项目:国家自然科学基金项目( 61271407,61301242);山东省自然 科学基金项目(ZR2013FQ015);中央高校基本科研业务费专 项资金资助项目(14CX06066A). 通信作者:王延江.E⁃mail: yjwang@ upc.edu.cn. 视觉图像的分类与识别研究是计算机视觉研 究、模式识别与机器学习领域内的一个非常活跃的 方向,其在许多领域中应用广泛,如银行系统的人 脸识别、防御系统的行人检测与跟踪、交通系统的 车牌检测与车辆跟踪等。 近年来,图像分类[1] 吸引 了研究者们的注意,关于视觉图像识别与分类的各 种理论与算法层出不穷,如最近邻分类器[2] 、神经 网络分类器[3-4] 、SVM 支持向量机分类器[5] 、卷积神 经网络分类器[6] 、ELM 极限学习机[7]及稀疏编码方 法等。 为获得良好的图像分类效果,研究者们在设 计图像分类方法及改进分类准确性方面都做了大 量工作。 例如,稀疏编码方法已被证实在图像分类 中具有优秀的分类性能,基于该方法的许多改进的 稀疏编码方法也被相继提出,如 SRC 方法[8] 、CRC 方法[9] 、RSC 方法[10] 及 RLRC 方法[11] 等。 尽管现 有的许多算法在图像分类方面表现突出,但目前已 有的识别分类算法大多侧重于“区别”,忽视了“认 识”,即侧重将某一类物体与有限类已学过物体进

第3期 姜英,等:REM记忆模型在图像分类识别中的应用 ·311· 行区分。然而人类认识事物的过程侧重于对某一 习、存储与提取方法。 类物体与无限类未知物体的区分,只在细小之处重 1图像特征表达 视“区别”(如区别桌子与椅子或者鱼与海豚等)。 对于首次遇到的从未学习过的物体,传统的模式识 图像特征提取在视觉图像学习过程中起着非 别方法会将其归类于某一个已学习的类别。但是 常关键的作用。近几年来,许多特征提取算法被陆 同样情况下,人类对首次遇到的新物体的直接反应 续提出并被应用于物体识别、如方向梯度直方图 是从未见过或者不认识该物体,而不是直接判断其 (HOG)等)、局部二值模式(LBP)[2]、尺度不变特 属于哪一类已经学习过的物体。众所周知,计算机 征转换(SIFT)【2、加速鲁棒特征(SURF)[2]等。其 视觉研究的主要目标是使计算机能像人类一样轻 中HOG算子能很好地描述局部目标的表现与形状, 易地识别视觉图像。神经生理学、心理学以及认知 LBP算子具有灰度尺度不变性和旋转不变性,本文 科学研究表明12-],人类能够轻易地将目标从周围 将这两种算子同时应用于图像特征提取以描述图 环境中识别出来与人类记忆机制有着非常密切的 像的形状与纹理特征。 联系。人们所看到的和所经历的都要经过记忆系 1.1HOG特征 统的处理。当认知新的事物时,与该事物相关的记 方向梯度直方图(histogram of oriented gradient, 忆信息就会被提取出来,从而加快认知的过程并适 HOG)特征是由N.Dalal等2]提出的一种物体特征 应新的环境。然而,在人脑记忆过程中信息是如何 描述子,其通过计算和统计图像局部区域的梯度方 被加工、存储和提取的仍然不得而知。Murdock[ 向直方图来构成特征。HOG特征提取算法的具体 认为现代人脑记忆建模理论至少要解释4个问题: 实现过程如图1所示。 信息是如何被表达、被存储与提取的信息的种类, 输入图像 存储与提取运算的本质以及信息存储的格式。围 绕这些问题研究人员提出了包括情景记忆、语义记 归一化图像 忆以及神经计算在内的记忆建模理论。Raaijmakers 等u)提出了SAM模型,所存储的信息用“记忆影 计算每个像素点的梯度方向与幅值 像”表达,能解释记忆研究中的列表强度效应、列表 对每个cll块的梯度直方图进行规定权重的投影 长度效应以及近因效应等,但无法解释镜像效应; 对每个重叠block块内的cell进行对比度归一化 Hintzman等[i6)提出的MINERVA2模型首次将情景 记忆与语义记忆联合用于提取建模,没有考虑列表 所有blok块内的直方图向量组成一个大的HOG特征向量 强度效应以及镜像效应:Shiffrin等]提出的REM 记忆模型,采用Bayesian理论计算线索与记忆影像 图1HOG特征提取算法流程 的似然度,用于匹配搜索。上述情景记忆模型均假 Fig.1 The flow chart of HOG algorithm 设识别判断是在整体匹配相似度强度的基础上完 1.2LBP特征 成的,其中REM记忆模型的突出性不仅因为其坚实 局部二值模式(LBP)是由T.Ojala、M.Pietikainen 的数学基础,也源于其可以解释情景记忆研究中出 和D.Harwood提出的一种灰度尺度不变性和旋转不 现的许多现象,如列表长度、列表强度与词汇频率 变性的纹理算子[)。原始LBP算子不能满足不同 效应等。REM模型对情景记忆研究中的列表强度 尺寸和频率纹理的需要,研究人员对其进行各种改进 效应、列表长度效应、词汇频率效应以及镜面效应 与优化,如半径为R的圆形区域内含有P个采样点 与正态ROC斜率效应的解释不仅吸引了众多研究 的LBP算子及LBP旋转不变算子]。T.Ojalat列 人员对REM模型的进一步研究-2],也引起了我 定义了一个等价模式,模式数量减少为种,特征向量 们的思考一能否将记忆模型应用于图像识别分 维数更少,减少了高频噪声带来的影响。 类中。目前大多数记忆模型均采用词汇列表的学 本文采用的LBP特征提取算法过程如下: 习方式,对自然图像的学习和分类研究得很少,因 1)对图像中的每一个像素点,定义圆形邻域窗 此本文尝试将REM模型引入视觉图像的存储与识 口,每个像素的灰度值与其相邻的8个像素的灰度值 别,并提出一种基于REM记忆模型的视觉图像的学 比较,若周围像素值大于中心像素值,则该像素点的
行区分。 然而人类认识事物的过程侧重于对某一 类物体与无限类未知物体的区分,只在细小之处重 视“区别”(如区别桌子与椅子或者鱼与海豚等)。 对于首次遇到的从未学习过的物体,传统的模式识 别方法会将其归类于某一个已学习的类别。 但是 同样情况下,人类对首次遇到的新物体的直接反应 是从未见过或者不认识该物体,而不是直接判断其 属于哪一类已经学习过的物体。 众所周知,计算机 视觉研究的主要目标是使计算机能像人类一样轻 易地识别视觉图像。 神经生理学、心理学以及认知 科学研究表明[12-13] ,人类能够轻易地将目标从周围 环境中识别出来与人类记忆机制有着非常密切的 联系。 人们所看到的和所经历的都要经过记忆系 统的处理。 当认知新的事物时,与该事物相关的记 忆信息就会被提取出来,从而加快认知的过程并适 应新的环境。 然而,在人脑记忆过程中信息是如何 被加工、存储和提取的仍然不得而知。 Murdock [14] 认为现代人脑记忆建模理论至少要解释 4 个问题: 信息是如何被表达、被存储与提取的信息的种类, 存储与提取运算的本质以及信息存储的格式。 围 绕这些问题研究人员提出了包括情景记忆、语义记 忆以及神经计算在内的记忆建模理论。 Raaijmakers 等[15]提出了 SAM 模型,所存储的信息用“记忆影 像”表达,能解释记忆研究中的列表强度效应、列表 长度效应以及近因效应等,但无法解释镜像效应; Hintzman 等[16]提出的 MINERVA 2 模型首次将情景 记忆与语义记忆联合用于提取建模,没有考虑列表 强度效应以及镜像效应;Shiffrin 等[17] 提出的 REM 记忆模型,采用 Bayesian 理论计算线索与记忆影像 的似然度,用于匹配搜索。 上述情景记忆模型均假 设识别判断是在整体匹配相似度强度的基础上完 成的,其中 REM 记忆模型的突出性不仅因为其坚实 的数学基础,也源于其可以解释情景记忆研究中出 现的许多现象,如列表长度、列表强度与词汇频率 效应等。 REM 模型对情景记忆研究中的列表强度 效应、列表长度效应、词汇频率效应以及镜面效应 与正态 ROC 斜率效应的解释不仅吸引了众多研究 人员对 REM 模型的进一步研究[18-21] ,也引起了我 们的思考———能否将记忆模型应用于图像识别分 类中。 目前大多数记忆模型均采用词汇列表的学 习方式,对自然图像的学习和分类研究得很少,因 此本文尝试将 REM 模型引入视觉图像的存储与识 别,并提出一种基于 REM 记忆模型的视觉图像的学 习、存储与提取方法。 1 图像特征表达 图像特征提取在视觉图像学习过程中起着非 常关键的作用。 近几年来,许多特征提取算法被陆 续提出并被应用于物体识别、如方向梯度直方图 (HOG)等[22] 、局部二值模式(LBP) [23] 、尺度不变特 征转换(SIFT) [24] 、加速鲁棒特征(SURF) [25] 等。 其 中 HOG 算子能很好地描述局部目标的表现与形状, LBP 算子具有灰度尺度不变性和旋转不变性,本文 将这两种算子同时应用于图像特征提取以描述图 像的形状与纹理特征。 1.1 HOG 特征 方向梯度直方图(histogram of oriented gradient, HOG)特征是由 N.Dalal 等[22] 提出的一种物体特征 描述子,其通过计算和统计图像局部区域的梯度方 向直方图来构成特征。 HOG 特征提取算法的具体 实现过程如图 1 所示。 图 1 HOG 特征提取算法流程 Fig.1 The flow chart of HOG algorithm 1.2 LBP 特征 局部二值模式(LBP)是由 T.Ojala、M.Pietikäinen 和 D. Harwood 提出的一种灰度尺度不变性和旋转不 变性的纹理算子[23] 。 原始 LBP 算子不能满足不同 尺寸和频率纹理的需要,研究人员对其进行各种改进 与优化,如半径为 R 的圆形区域内含有 P 个采样点 的 LBP 算子及 LBP 旋转不变算子[26] 。 T. Ojala [27] 定义了一个等价模式,模式数量减少为 种,特征向量 维数更少,减少了高频噪声带来的影响。 本文采用的 LBP 特征提取算法过程如下: 1)对图像中的每一个像素点,定义圆形邻域窗 口,每个像素的灰度值与其相邻的 8 个像素的灰度值 比较,若周围像素值大于中心像素值,则该像素点的 第 3 期 姜英,等:REM 记忆模型在图像分类识别中的应用 ·311·

·312· 智能系统学报 第12卷 位置被标记为1,否则为0。这样可产生8位二进制 特征值向量的一个不完整且容易出错的复制。本文 数,即得到该窗口中心像素点的初始LBP值。 试图借鉴REM模型对单词的存储学习过程来模拟人 2)不断旋转圆形邻域得到一系列初始定义的 脑对图像的学习过程,有概率地对图像的特征向量进 LBP值,取最小值作为该像素点的LBP值。 行复制,同时在复制过程中允许出现错误值。 3)统计LBP值对应的二进制数从0~1或1~0 从图像库中选取图像,提取图像LBP与HOG特 跳变的次数,根据跳变次数确定其属于哪一种LBP 征,将其分别写成行向量形式并连接起来生成图像特 模式,共有P+1=9种模式,得到的模式数值即为像素 征向量。HOG特征是由小数组成的,并不是非负整 点的LBP值。 数,为方便REM模型的计算,在实验中简单地对该特 4)图像中所有像素点的LBP值组合起来形成一 征扩大10倍并四舍五入。每学习一次图像特征向 个LBP特征矩阵,即为该图像的LBP特征。 量,对于那些还没有存储任何信息的位置,存储新信 2REM模型在视觉图像的表达、 息的概率为u·。注意到,一旦某个值被存储,之后该 值不会改变。如果对某个特征有存储,其特征值从已 存储与提取中的应用 学向量中正确复制的概率是c,以1-c的概率根据P 认知记忆的快速提取模型一REM模型是 [V=j]=(1-g)g,j=1,2,…,∞随机取值,并允许偶 Shiffrin等[1997年提出的一个用于识别单词的记 然选取正确值的可能性。 忆模型,该模型采用Bayesian理论计算线索与记忆影 用V={V,=12N标记所有已学习图像的特征 像的似然度,用于匹配搜索。该模型能够解释许多情 集,其中V,表示已学习图像集合中第j副图像L的特 景记忆研究中的一些科学现象,如列表强度效应、列 征向量,N为已学习图像集合中的图像个数。 表长度效应、词汇频率效应、镜面效应与正态ROC斜 2.2提取 率效应;其与SAM、MINERVA2模型的主要区别之一 给定要检测的图像It,将其特征向量Va与V= 在于,其实现了似然率的贝叶斯计算,是国际上公认 {V1.2…进行匹配,匹配结果为D={D,=12…, 的最好的记忆模型之一。 其中D,为被检测图像特征与第j个视觉图像特征的 REM记忆模型被提出之后,研究人员陆续对 匹配结果。用s图像表示与被检测图像相同的存储 REM模型进行研究。Stams等18]通过对编码与提取 图像,d图像表示除被检测图像之外的其他视觉图像 过程中的项目强度的控制,对比研究了REM模型与 的存储图像。 BCDMEM模型对提取过程中项目强度对误报率降低 被检测图像I与第j幅已存储图像I,的匹配过 的解释说明。Cox等I]在REM与RCA-REM模型基 程的关键步骤是,计算似然率入,即在观测结果D,基 础上提出一个新认知记忆模型,证实了即使在任务、 础上第j幅图像为s图像与d图像的概率比值: 学习因素、刺激及其他因子变化情况下,所提方法都 P(D S) 有可能获得合理的认知决策。Criss等[0]对比了 入= P(D:N) REM模型与SLiM(the subjective likelihood model)模 型,发现REM模型预测的误报率较高;M.Montenegro (1-c)%Πe+(1-c)g(1-g)- (1) keM g(1-g)'g 等2研究了REM模型的解析表达式,文中引入 式中:S,为第j副图像为s图像的事件;V为第j副图 Fourier变换,给出REM模型的FT积分方程,导出在 像为d图像的事件:M为非零特征值与被检测向量特 给定参数值下模型预测的命中率与误报率的双积分 征值匹配的目录;V为第j副图像中第k个特征值; 形式的解析表达式,同时发现其具有与BCDMEM模 nn为V与V不匹配的非零特征值个数;g为几何分 型相同的一些性质:模型是不确定的,除非其中的一 布参数。 个参数固定为一个预设值,向量长度参数是不可忽略 2.3 Bayesian决策 的参数。 给定探测图像I,将其与所有已学习图像I= 2.1特征表达与存储 {L=1.2.…进行匹配与不匹配比较,计算对应的似然 REM模型指出人脑记忆由图像构成,每幅图像 值入={入1,入2,…,入x},进而得到被检测图像为旧的 是由一个特征值向量表示的,并且最终存储结果是对 而非新的概率为
位置被标记为 1,否则为 0。 这样可产生 8 位二进制 数,即得到该窗口中心像素点的初始 LBP 值。 2)不断旋转圆形邻域得到一系列初始定义的 LBP 值,取最小值作为该像素点的 LBP 值。 3)统计 LBP 值对应的二进制数从 0 ~ 1 或 1 ~ 0 跳变的次数,根据跳变次数确定其属于哪一种 LBP 模式,共有 P+1= 9 种模式,得到的模式数值即为像素 点的 LBP 值。 4)图像中所有像素点的 LBP 值组合起来形成一 个 LBP 特征矩阵,即为该图像的 LBP 特征。 2 REM 模型在视觉图像的表达、 存储与提取中的应用 认知记忆的快速提取模型———REM 模型是 Shiffrin 等[17] 1997 年提出的一个用于识别单词的记 忆模型,该模型采用 Bayesian 理论计算线索与记忆影 像的似然度,用于匹配搜索。 该模型能够解释许多情 景记忆研究中的一些科学现象,如列表强度效应、列 表长度效应、词汇频率效应、镜面效应与正态 ROC 斜 率效应;其与 SAM、MINERVA2 模型的主要区别之一 在于,其实现了似然率的贝叶斯计算,是国际上公认 的最好的记忆模型之一。 REM 记忆模型被提出之后,研究人员陆续对 REM 模型进行研究。 Stams 等[18] 通过对编码与提取 过程中的项目强度的控制,对比研究了 REM 模型与 BCDMEM 模型对提取过程中项目强度对误报率降低 的解释说明。 Cox 等[19]在 REM 与 RCA⁃REM 模型基 础上提出一个新认知记忆模型,证实了即使在任务、 学习因素、刺激及其他因子变化情况下,所提方法都 有可能获得合理的认知决策。 Criss 等[20] 对比了 REM 模型与 SLiM(the subjective likelihood model)模 型,发现 REM 模型预测的误报率较高;M.Montenegro 等[21]研究了 REM 模型的解析表达式,文中引入 Fourier 变换,给出 REM 模型的 FT 积分方程,导出在 给定参数值下模型预测的命中率与误报率的双积分 形式的解析表达式,同时发现其具有与 BCDMEM 模 型相同的一些性质:模型是不确定的,除非其中的一 个参数固定为一个预设值,向量长度参数是不可忽略 的参数。 2.1 特征表达与存储 REM 模型指出人脑记忆由图像构成,每幅图像 是由一个特征值向量表示的,并且最终存储结果是对 特征值向量的一个不完整且容易出错的复制。 本文 试图借鉴 REM 模型对单词的存储学习过程来模拟人 脑对图像的学习过程,有概率地对图像的特征向量进 行复制,同时在复制过程中允许出现错误值。 从图像库中选取图像,提取图像 LBP 与 HOG 特 征,将其分别写成行向量形式并连接起来生成图像特 征向量。 HOG 特征是由小数组成的,并不是非负整 数,为方便 REM 模型的计算,在实验中简单地对该特 征扩大 10 倍并四舍五入。 每学习一次图像特征向 量,对于那些还没有存储任何信息的位置,存储新信 息的概率为 u ∗ 。 注意到,一旦某个值被存储,之后该 值不会改变。 如果对某个特征有存储,其特征值从已 学向量中正确复制的概率是 c,以 1-c 的概率根据 P [V=j] = (1-g) j-1 g,j = 1,2,…,¥随机取值,并允许偶 然选取正确值的可能性。 用 V={Vj}j = 1,2,…,N标记所有已学习图像的特征 集,其中 Vj表示已学习图像集合中第 j 副图像 Ij 的特 征向量,N 为已学习图像集合中的图像个数。 2.2 提取 给定要检测的图像 Itest,将其特征向量 Vtest与V= {Vj}j = 1,2,…,N进行匹配,匹配结果为 D = {Dj }j = 1,2,…,N, 其中 Dj 为被检测图像特征与第 j 个视觉图像特征的 匹配结果。 用 s 图像表示与被检测图像相同的存储 图像,d 图像表示除被检测图像之外的其他视觉图像 的存储图像。 被检测图像 Itest与第 j 幅已存储图像 Ij 的匹配过 程的关键步骤是,计算似然率 λj,即在观测结果 Dj 基 础上第 j 幅图像为 s 图像与 d 图像的概率比值: λj = P(Dj Sj) P(Dj Nj) = (1 - c) njq ∏k∈M c + (1 - c)g (1 - g) Vkj -1 g (1 - g) Vkj -1 (1) 式中:Sj 为第 j 副图像为 s 图像的事件;Nj为第 j 副图 像为 d 图像的事件;M 为非零特征值与被检测向量特 征值匹配的目录;Vkj为第 j 副图像中第 k 个特征值; njq为 Vj与 Vtest不匹配的非零特征值个数;g 为几何分 布参数。 2.3 Bayesian 决策 给定探测图像 Itest,将其与所有已学习图像 I = {Ij}j = 1,2,…,N进行匹配与不匹配比较,计算对应的似然 值 λ={λ1 ,λ2 ,…,λN },进而得到被检测图像为旧的 而非新的概率为 ·312· 智 能 系 统 学 报 第 12 卷
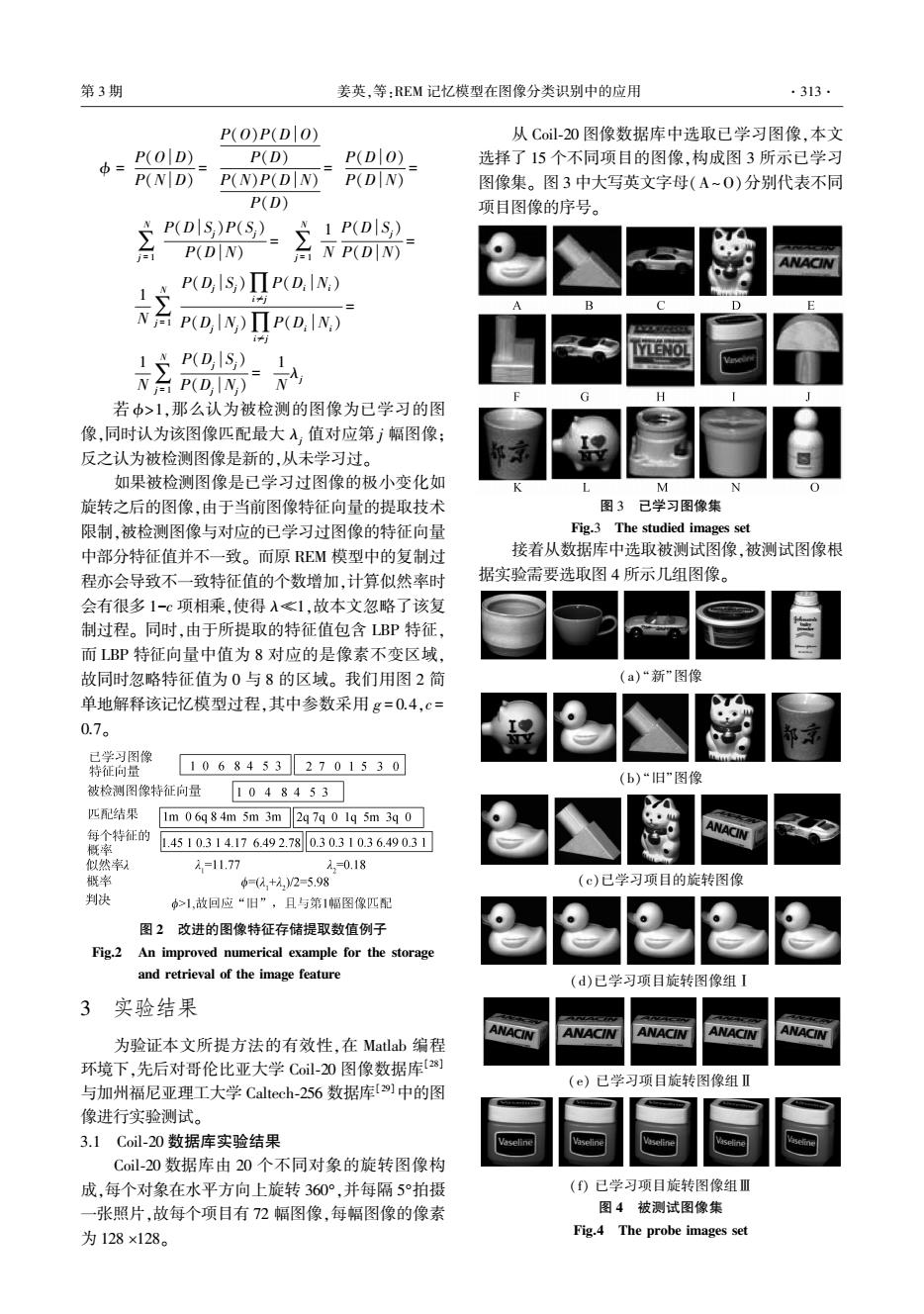
第3期 姜英,等:REM记忆模型在图像分类识别中的应用 ·313· P(O)P(D O) 从Col-20图像数据库中选取已学习图像,本文 中= P(O D) P(D) P(DO) 选择了15个不同项目的图像,构成图3所示已学习 P(N D) P(N)P(DN) P(D N) 图像集。图3中大写英文字母(A~0)分别代表不同 P(D) 项目图像的序号。 P(D S)P(S) 1 P(D S) P(D N) N P(D N) ANACIN P(D,lS)ΠP(D,lN) 三nNn网 B P(DS,)1 G H 若中>1,那么认为被检测的图像为已学习的图 像,同时认为该图像匹配最大入,值对应第j幅图像; 反之认为被检测图像是新的,从未学习过。 如果被检测图像是已学习过图像的极小变化如 M N 旋转之后的图像,由于当前图像特征向量的提取技术 图3已学习图像集 限制,被检测图像与对应的已学习过图像的特征向量 Fig.3 The studied images set 中部分特征值并不一致。而原REM模型中的复制过 接着从数据库中选取被测试图像,被测试图像根 程亦会导致不一致特征值的个数增加,计算似然率时 据实验需要选取图4所示几组图像。 会有很多1-℃项相乘,使得入≤1,故本文忽略了该复 制过程。同时,由于所提取的特征值包含LBP特征, 而LBP特征向量中值为8对应的是像素不变区域, 故同时忽略特征值为0与8的区域。我们用图2简 (a)“新”图像 单地解释该记忆模型过程,其中参数采用g=0.4,c= 0.7。 已学习图像 特征向量 10684532701530 (b)“旧”图像 被检测图像特征向量 1048453 匹配结果 1m 06q 8 4m 5m 3m2q 7q 0 1q 5m 3q 0 每个特征的 概率 1.4510.314.176.492.780.30.310.36.490.31 ANACIN 似然率 2=11.77 入30.18 概率 =(1+元,)/2=5.98 (c)已学习项目的旋转图像 判决 >1,故回应“旧”,且与第1幅图像匹配 图2改进的图像特征存储提取数值例子 Fig.2 An improved numerical example for the storage and retrieval of the image feature (d)已学习项目旋转图像组I 3实验结果 ANACIN ANACIN ANACIN ANACIN ANACIN 为验证本文所提方法的有效性,在Matlab编程 环境下,先后对哥伦比亚大学Coil-20图像数据库[2] (e)已学习项目旋转图像组Ⅱ 与加州福尼亚理工大学Caltech-256数据库]中的图 像进行实验测试。 3.1Coil-20数据库实验结果 Coil-20数据库由20个不同对象的旋转图像构 成,每个对象在水平方向上旋转360°,并每隔5°拍摄 ()已学习项目旋转图像组Ⅲ 一张照片,故每个项目有72幅图像,每幅图像的像素 图4被测试图像集 为128×128。 Fig.4 The probe images set
ϕ = P(O D) P(N D) = P(O)P(D O) P(D) P(N)P(D N) P(D) = P(D O) P(D N) = ∑ N j = 1 P(D Sj)P(Sj) P(D N) = ∑ N j = 1 1 N P(D Sj) P(D N) = 1 N∑ N j = 1 P(Dj Sj)∏i≠j P(Di Ni) P(Dj Nj)∏i≠j P(Di Ni) = 1 N∑ N j = 1 P(Dj Sj) P(Dj Nj) = 1 N λj 若 ϕ>1,那么认为被检测的图像为已学习的图 像,同时认为该图像匹配最大 λj 值对应第 j 幅图像; 反之认为被检测图像是新的,从未学习过。 如果被检测图像是已学习过图像的极小变化如 旋转之后的图像,由于当前图像特征向量的提取技术 限制,被检测图像与对应的已学习过图像的特征向量 中部分特征值并不一致。 而原 REM 模型中的复制过 程亦会导致不一致特征值的个数增加,计算似然率时 会有很多 1-c 项相乘,使得 λ≪1,故本文忽略了该复 制过程。 同时,由于所提取的特征值包含 LBP 特征, 而 LBP 特征向量中值为 8 对应的是像素不变区域, 故同时忽略特征值为 0 与 8 的区域。 我们用图 2 简 单地解释该记忆模型过程,其中参数采用 g = 0.4,c = 0.7。 图 2 改进的图像特征存储提取数值例子 Fig.2 An improved numerical example for the storage and retrieval of the image feature 3 实验结果 为验证本文所提方法的有效性,在 Matlab 编程 环境下,先后对哥伦比亚大学 Coil⁃20 图像数据库[28] 与加州福尼亚理工大学 Caltech⁃256 数据库[29]中的图 像进行实验测试。 3.1 Coil⁃20 数据库实验结果 Coil⁃20 数据库由 20 个不同对象的旋转图像构 成,每个对象在水平方向上旋转 360°,并每隔 5°拍摄 一张照片,故每个项目有 72 幅图像,每幅图像的像素 为 128 ´128。 从 Coil⁃20 图像数据库中选取已学习图像,本文 选择了 15 个不同项目的图像,构成图 3 所示已学习 图像集。 图 3 中大写英文字母(A~O)分别代表不同 项目图像的序号。 图 3 已学习图像集 Fig.3 The studied images set 接着从数据库中选取被测试图像,被测试图像根 据实验需要选取图 4 所示几组图像。 (a)“新”图像 (b)“旧”图像 (c)已学习项目的旋转图像 (d)已学习项目旋转图像组Ⅰ (e) 已学习项目旋转图像组Ⅱ (f) 已学习项目旋转图像组Ⅲ 图 4 被测试图像集 Fig.4 The probe images set 第 3 期 姜英,等:REM 记忆模型在图像分类识别中的应用 ·313·
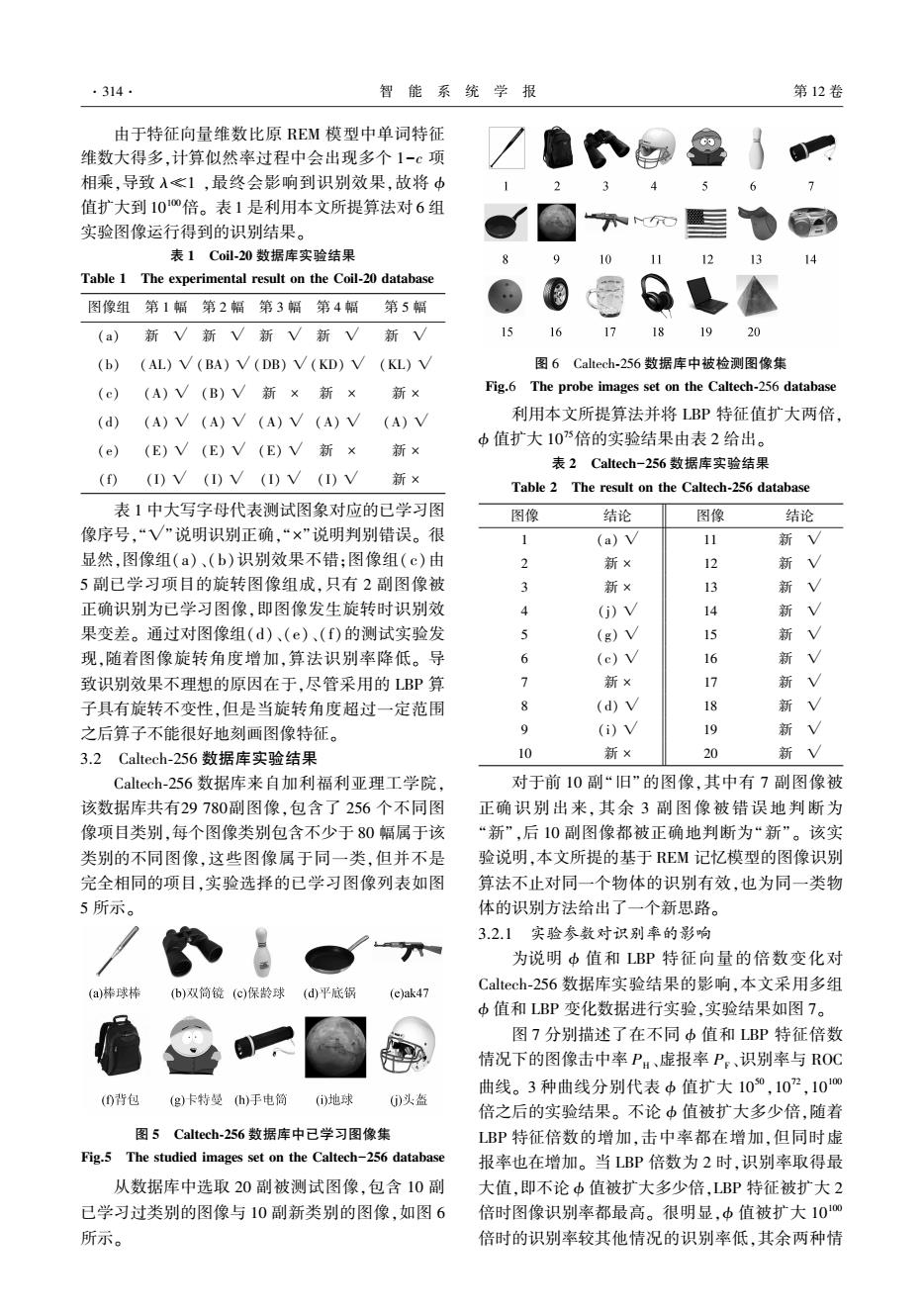
·314. 智能系统学报 第12卷 由于特征向量维数比原REM模型中单词特征 维数大得多,计算似然率过程中会出现多个1-c项 相乘,导致入≤1,最终会影响到识别效果,故将中 值扩大到100倍。表1是利用本文所提算法对6组 实验图像运行得到的识别结果。 表1Coil-20数据库实验结果 9 10 12 13 Table 1 The experimental result on the Coil-20 database 图像组第1幅第2幅第3幅第4幅第5幅 (a)新V新V新V新V新√ 15 16 17 18 19 20 (b)(AL)V(BA)V(DB)V(KD)V (KL)V 图6 Caltech-256数据库中被检测图像集 (c)(A)V(B)V新×新×新× Fig.6 The probe images set on the Caltech-256 database (a)(A)V (A)V (A)V (A)V (A)V 利用本文所提算法并将LBP特征值扩大两倍, (e)(E)√(E)V(E)V新×新× 中值扩大105倍的实验结果由表2给出。 表2 Caltech-256数据库实验结果 (n (1)V (1)V (1)V (1)V 新× Table 2 The result on the Caltech-256 database 表1中大写字母代表测试图象对应的已学习图 图像 结论 图像 结论 像序号,“√”说明识别正确,“×”说明判别错误。很 1 (a)v 11 新V 显然,图像组(a)、(b)识别效果不错:图像组(c)由 2 新× 12 新V 5副已学习项目的旋转图像组成,只有2副图像被 新× 13 新√ 正确识别为已学习图像,即图像发生旋转时识别效 4 (j)V 14 新 果变差。通过对图像组(d)、(e)、(f)的测试实验发 (g)V 小 新V 现,随着图像旋转角度增加,算法识别率降低。导 6 (e)v 16 新 V 致识别效果不理想的原因在于,尽管采用的LBP算 7 新× 17 新 子具有旋转不变性,但是当旋转角度超过一定范围 (d)v 18 新 之后算子不能很好地刻画图像特征。 9 (i)v 9 新V 3.2 Caltech-256数据库实验结果 10 新× 20 新V Caltech-256数据库来自加利福利亚理工学院, 对于前10副“旧”的图像,其中有7副图像被 该数据库共有29780副图像,包含了256个不同图 正确识别出来,其余3副图像被错误地判断为 像项目类别,每个图像类别包含不少于80幅属于该 “新”,后10副图像都被正确地判断为“新”。该实 类别的不同图像,这些图像属于同一类,但并不是 验说明,本文所提的基于REM记忆模型的图像识别 完全相同的项目,实验选择的已学习图像列表如图 算法不止对同一个物体的识别有效,也为同一类物 5所示。 体的识别方法给出了一个新思路。 3.2.1实验参数对识别率的影响 为说明中值和LBP特征向量的倍数变化对 a)棒球棒 (b)双简镜(c)保龄球(d)平底锅 (c)ak47 Caltech-256数据库实验结果的影响,本文采用多组 中值和LBP变化数据进行实验,实验结果如图7。 图7分别描述了在不同中值和LBP特征倍数 情况下的图像击中率P:、虚报率P。、识别率与ROC 曲线。3种曲线分别代表中值扩大100,102,1010 ()背包 (g)卡特曼h)手电筒 ()地球 ()头盔 倍之后的实验结果。不论中值被扩大多少倍,随着 图5 Caltech-256数据库中已学习图像集 LBP特征倍数的增加,击中率都在增加,但同时虚 Fig.5 The studied images set on the Caltech-256 database 报率也在增加。当LBP倍数为2时,识别率取得最 从数据库中选取20副被测试图像,包含10副 大值,即不论b值被扩大多少倍,LBP特征被扩大2 已学习过类别的图像与10副新类别的图像,如图6 倍时图像识别率都最高。很明显,中值被扩大101 所示。 倍时的识别率较其他情况的识别率低,其余两种情
由于特征向量维数比原 REM 模型中单词特征 维数大得多,计算似然率过程中会出现多个 1-c 项 相乘,导致 λ≪1 ,最终会影响到识别效果,故将 ϕ 值扩大到 10 100倍。 表 1 是利用本文所提算法对 6 组 实验图像运行得到的识别结果。 表 1 Coil⁃20 数据库实验结果 Table 1 The experimental result on the Coil⁃20 database 图像组 第 1 幅 第 2 幅 第 3 幅 第 4 幅 第 5 幅 (a) 新 √ 新 √ 新 √ 新 √ 新 √ (b) (AL) √ (BA) √ (DB) √ (KD) √ (KL) √ (c) (A) √ (B) √ 新 × 新 × 新 × (d) (A) √ (A) √ (A) √ (A) √ (A) √ (e) (E) √ (E) √ (E) √ 新 × 新 × (f) (I) √ (I) √ (I) √ (I) √ 新 × 表 1 中大写字母代表测试图象对应的已学习图 像序号,“√”说明识别正确,“×”说明判别错误。 很 显然,图像组(a)、(b)识别效果不错;图像组( c)由 5 副已学习项目的旋转图像组成,只有 2 副图像被 正确识别为已学习图像,即图像发生旋转时识别效 果变差。 通过对图像组(d)、(e)、(f)的测试实验发 现,随着图像旋转角度增加,算法识别率降低。 导 致识别效果不理想的原因在于,尽管采用的 LBP 算 子具有旋转不变性,但是当旋转角度超过一定范围 之后算子不能很好地刻画图像特征。 3.2 Caltech⁃256 数据库实验结果 Caltech⁃256 数据库来自加利福利亚理工学院, 该数据库共有29 780副图像,包含了 256 个不同图 像项目类别,每个图像类别包含不少于 80 幅属于该 类别的不同图像,这些图像属于同一类,但并不是 完全相同的项目,实验选择的已学习图像列表如图 5 所示。 图 5 Caltech⁃256 数据库中已学习图像集 Fig.5 The studied images set on the Caltech-256 database 从数据库中选取 20 副被测试图像,包含 10 副 已学习过类别的图像与 10 副新类别的图像,如图 6 所示。 图 6 Caltech⁃256 数据库中被检测图像集 Fig.6 The probe images set on the Caltech⁃256 database 利用本文所提算法并将 LBP 特征值扩大两倍, ϕ 值扩大 10 75倍的实验结果由表 2 给出。 表 2 Caltech-256 数据库实验结果 Table 2 The result on the Caltech⁃256 database 图像 结论 图像 结论 1 (a) √ 11 新 √ 2 新 × 12 新 √ 3 新 × 13 新 √ 4 (j) √ 14 新 √ 5 (g) √ 15 新 √ 6 (c) √ 16 新 √ 7 新 × 17 新 √ 8 (d) √ 18 新 √ 9 (i) √ 19 新 √ 10 新 × 20 新 √ 对于前 10 副“旧”的图像,其中有 7 副图像被 正确识别出来, 其余 3 副图像被错误地判断为 “新”,后 10 副图像都被正确地判断为“新”。 该实 验说明,本文所提的基于 REM 记忆模型的图像识别 算法不止对同一个物体的识别有效,也为同一类物 体的识别方法给出了一个新思路。 3.2.1 实验参数对识别率的影响 为说明 ϕ 值和 LBP 特征向量的倍数变化对 Caltech⁃256 数据库实验结果的影响,本文采用多组 ϕ 值和 LBP 变化数据进行实验,实验结果如图 7。 图 7 分别描述了在不同 ϕ 值和 LBP 特征倍数 情况下的图像击中率 PH 、虚报率 PF 、识别率与 ROC 曲线。 3 种曲线分别代表 ϕ 值扩大 10 50 ,10 72 ,10 100 倍之后的实验结果。 不论 ϕ 值被扩大多少倍,随着 LBP 特征倍数的增加,击中率都在增加,但同时虚 报率也在增加。 当 LBP 倍数为 2 时,识别率取得最 大值,即不论 ϕ 值被扩大多少倍,LBP 特征被扩大 2 倍时图像识别率都最高。 很明显,ϕ 值被扩大 10 100 倍时的识别率较其他情况的识别率低,其余两种情 ·314· 智 能 系 统 学 报 第 12 卷